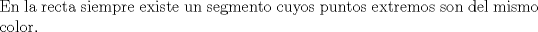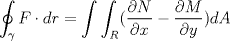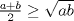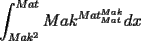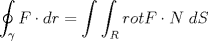|
|
|
|
|
|
|
  |
 Mar 1 2007, 05:10 PM Mar 1 2007, 05:10 PM
Publicado:
#1
|
|
 Dios Matemático Supremo Grupo: Usuario FMAT Mensajes: 558 Registrado: 14-May 05 Desde: Maipú, Stgo, Chile Miembro Nº: 27 Nacionalidad:  Colegio/Liceo:  Universidad:  Sexo:  |
16ª OLIMPIADA NACIONAL DE MATEMÁTICAS Prueba Final, Nivel Mayor Primera Prueba Problema 1: Una empresa con 2004 trabajadores,celebro su aniversario invitando a todos a un almuerzo servido en una mesa redonda.Cuando se sentaron alrededor de esta mesa los 2004 trabajadores, formaron un circulo de personas y al poco tiempo descubrieron que todos ellos tenían salario distinto y ademas que la diferencia entre los sueldos de dos vecinos cualesquiera,en la mesa redonda,era de 2000 o bien 3000 pesos. Calcule la maxima diferencia que puede haber entre los sueldos de estos trabajadores. Problema 2: Todo punto de una recta esta pintado de color rojo o bien de color azul. Demuestre que siempre existen tres puntos 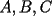 que estan pintados de igual color y son tales que el punto que estan pintados de igual color y son tales que el punto 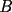 es el punto medio del segmento es el punto medio del segmento 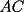 . .Problema 3: El perimetro,es decir, la suma de las longitudes de todos los lados de un cuadrilatero convexo 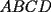 , es igual a 2004 metros; mientras que la longitud de su diagonal , es igual a 2004 metros; mientras que la longitud de su diagonal 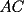 es igual a 1001 metros. Investigue si la longitud de la otra diagonal es igual a 1001 metros. Investigue si la longitud de la otra diagonal 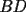 puede: puede:a) Ser igual a solo un metro. b) Ser igual a la longitud de la diagonal 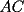 . .Segunda Prueba Problema 4: Se toma el numero 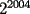 y se calcula la suma y se calcula la suma 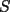 de todos sus digitos. Luego se calcula la suma de todos los digitos de de todos sus digitos. Luego se calcula la suma de todos los digitos de 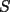 para obtener para obtener 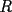 . A continuacion se calcula la suma de todos los digitos de . A continuacion se calcula la suma de todos los digitos de 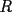 y asi sucesivamentehasta llegar a un numero de un solo digito. Encuentrelo.(Por ejemplo si tomamos y asi sucesivamentehasta llegar a un numero de un solo digito. Encuentrelo.(Por ejemplo si tomamos 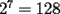 , encontramos que , encontramos que 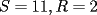 . Asi en este caso de . Asi en este caso de 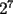 el digito buscado será 2). el digito buscado será 2).Problema 5: Sobre la superficie infinita del mar flota una mancha de petroleo negra y acotada. Al cabo de cada minuto la mancha y el mar cambian segun la sigueinte ley: en cada punto 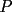 del mar (o de la mancha), se considera un disco del mar (o de la mancha), se considera un disco 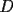 de radio 1 centrado en de radio 1 centrado en 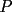 . Si mas de la mitad del área dentro del disco . Si mas de la mitad del área dentro del disco 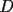 tiene color negro, el punto tiene color negro, el punto 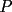 permanecera negro durante el proximo minuto. Si mas de la mitad del área dentro del disco permanecera negro durante el proximo minuto. Si mas de la mitad del área dentro del disco 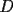 está de color azul marino, el punto está de color azul marino, el punto 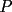 tendra color azul marino durante el minuto siguiente. En el caso de que tanto el área limpia como la contaminada dentro del disco tendra color azul marino durante el minuto siguiente. En el caso de que tanto el área limpia como la contaminada dentro del disco 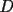 sean iguales, su centro sean iguales, su centro 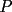 no cambiara de color. ¿Puede aquella mancha "vivir" siempre o desaparecera en algun momento? no cambiara de color. ¿Puede aquella mancha "vivir" siempre o desaparecera en algun momento?Problema 6: Los segmentos 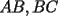 y y 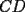 de la poligonal de la poligonal 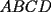 tienen la misma longitud y son tangentes a una circunferencia tienen la misma longitud y son tangentes a una circunferencia 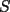 , de centro el punto , de centro el punto 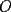 . Sea . Sea 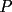 el punto de tangencia de el punto de tangencia de 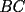 con con 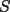 , y sea , y sea 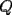 el punto de interseccion de las rectas el punto de interseccion de las rectas 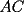 y y 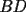 . Demuestre que el punto . Demuestre que el punto 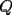 es colineal con los puntos es colineal con los puntos 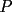 y y 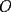 . .
-------------------- El peor defecto del ignorante es que ignora su propia ignorancia................
|
|
|
|
 Mar 8 2007, 01:53 PM Mar 8 2007, 01:53 PM
Publicado:
#2
|
|
 Dios Matemático Grupo: Usuario FMAT Mensajes: 374 Registrado: 16-September 06 Desde: New Haven, CT, USA. Miembro Nº: 2.275 Nacionalidad:  Colegio/Liceo:  Universidad:  Sexo:  |
CITA(Gp20 @ Mar 1 2007, 06:10 PM) Problema 4: Se toma el numero 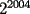 y se calcula la suma y se calcula la suma 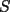 de todos sus digitos. Luego se calcula la suma de todos los digitos de de todos sus digitos. Luego se calcula la suma de todos los digitos de 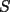 para obtener para obtener 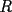 . A continuacion se calcula la suma de todos los digitos de . A continuacion se calcula la suma de todos los digitos de 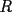 y asi sucesivamentehasta llegar a un numero de un solo digito. Encuentrelo.(Por ejemplo si tomamos y asi sucesivamentehasta llegar a un numero de un solo digito. Encuentrelo.(Por ejemplo si tomamos 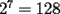 , encontramos que , encontramos que 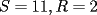 . Asi en este caso de . Asi en este caso de 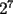 el digito buscado será 2). el digito buscado será 2).Solución Problema 4:  Saludos |
|
|
|
 Mar 8 2007, 05:44 PM Mar 8 2007, 05:44 PM
Publicado:
#3
|
|
 Dios Matemático Grupo: Usuario FMAT Mensajes: 374 Registrado: 16-September 06 Desde: New Haven, CT, USA. Miembro Nº: 2.275 Nacionalidad:  Colegio/Liceo:  Universidad:  Sexo:  |
CITA(Gp20 @ Mar 1 2007, 06:10 PM) Problema 6: Los segmentos 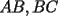 y y 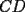 de la poligonal de la poligonal 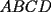 tienen la misma longitud y son tangentes a una circunferencia tienen la misma longitud y son tangentes a una circunferencia 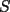 , de centro el punto , de centro el punto 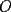 . Sea . Sea 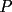 el punto de tangencia de el punto de tangencia de 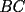 con con 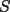 , y sea , y sea 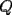 el punto de interseccion de las rectas el punto de interseccion de las rectas 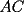 y y 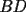 . Demuestre que el punto . Demuestre que el punto 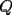 es colineal con los puntos es colineal con los puntos 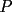 y y 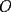 . .Solución problema 6:  screen.width*0.6) {this.resized=true; this.width=screen.width*0.4; this.alt='Pincha Aqui para ver esta imagen en su tamaño original';}" onmouseover="if(this.resized) this.style.cursor='hand';" onclick="if(this.resized) {window.open('http://img73.imageshack.us/img73/7367/colinealnm6.png');}" /> screen.width*0.6) {this.resized=true; this.width=screen.width*0.4; this.alt='Pincha Aqui para ver esta imagen en su tamaño original';}" onmouseover="if(this.resized) this.style.cursor='hand';" onclick="if(this.resized) {window.open('http://img73.imageshack.us/img73/7367/colinealnm6.png');}" />![TEX: \[<br />\begin{gathered}<br /> {\text{Tracemos las rectas AC}}{\text{,BD}}{\text{,BO}}{\text{,CO sean AB}} \cap {\text{S = E ; CD}} \cap {\text{S = G ; BO}} \cap {\text{AC = F ; }} \hfill \\<br /> {\text{CO}} \cap {\text{BD = H}}{\text{. Tambien trazamos EP}}{\text{,PG}}{\text{,FH}}{\text{,QO}}{\text{,QP}}{\text{.}} \hfill \\<br /> {\text{Sabemos que AB = BC = CD}} \Rightarrow \angle BAC = \angle BCA = \angle BEP = \angle BPE = \alpha ; \hfill \\<br /> \angle CBD = \angle CDB = \angle CPG = \angle CGP = \beta ({\text{isoceles}}) \Rightarrow EP{\text{ paralela AC}}{\text{, PG paralela BD}} \hfill \\<br /> {\text{Notemos que }}\vartriangle BPO \cong \vartriangle BEO \Rightarrow BO{\text{ bisectriz de }}\angle {\text{EBP}} \Rightarrow {\text{BO simetral de EP}}{\text{, }} \hfill \\<br /> {\text{BO simetral de }}AC.{\text{ Analogamente CO simetral de PG y BD}}{\text{. Luego como }} \hfill \\<br /> \angle {\text{QFO = }}\angle {\text{QHO = 90}} \hfill \\<br /> \Rightarrow {\text{OFQH es ciclico y BFHC es ciclico}} \hfill \\<br /> \Rightarrow \angle {\text{CBH = }}\angle {\text{CBD = }}\angle {\text{CFH = }}\beta \Rightarrow \angle QFH = \angle CFH = \angle QOH = \beta \hfill \\<br /> {\text{Como OG}} \bot {\text{CD}} \Rightarrow \angle {\text{PGO = 90 - }}\beta \Rightarrow \angle QOC = \beta \Rightarrow \angle COQ = \angle QOC \hfill \\<br /> {\text{Pero como CPO}} \cong CGO \Rightarrow \angle COG = \angle COP = \beta ,{\text{ Finalmente }}\angle COP = \angle COQ \hfill \\<br /> {\text{Demostrando que O}}{\text{,Q}}{\text{,P estan alineados}}{\text{.}} \hfill \\ <br />\end{gathered} <br />\]](./tex/10000000001490.gif) Saludos |
|
|
|
 Sep 6 2009, 04:42 PM Sep 6 2009, 04:42 PM
Publicado:
#4
|
|
 Dios Matemático Supremo Grupo: Usuario FMAT Mensajes: 1.564 Registrado: 12-November 07 Desde: La Union, XIV Region de los Rios Miembro Nº: 12.607 Nacionalidad:  Colegio/Liceo:  Universidad:  Sexo:  |
Problema 1:

-------------------- Ricardo Vargas Obando
Ex-alumno Deutsche Schule La Unión (Generación 2010, de los 150 años). Novato de Licenciatura en Matemática/Estadística, en la Pontificia Universidad Católica de Chile.  Grupo de facebook de Novatos Matemática y Estadística PUC 2011 Currículum Olímpico:
|
|
|
|
 Dec 6 2009, 04:40 PM Dec 6 2009, 04:40 PM
Publicado:
#5
|
|
 Dios Matemático Supremo Grupo: Moderador Mensajes: 590 Registrado: 14-October 07 Miembro Nº: 11.310 Colegio/Liceo:  Universidad:  Sexo:  |
Problema 2:
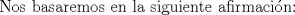  puntos1.png ( 25.63k )
Número de descargas: 11
puntos1.png ( 25.63k )
Número de descargas: 11 Lindo problema -------------------- |
|
|
|
 Oct 12 2010, 06:14 PM Oct 12 2010, 06:14 PM
Publicado:
#6
|
|
 Dios Matemático Supremo Grupo: Team Ensayos FMAT Mensajes: 1.559 Registrado: 18-November 07 Miembro Nº: 12.754 Nacionalidad:  Sexo:  |
Problema 4: Se toma el numero 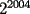 y se calcula la suma y se calcula la suma 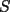 de todos sus digitos. Luego se calcula la suma de todos los digitos de de todos sus digitos. Luego se calcula la suma de todos los digitos de 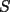 para obtener para obtener 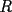 . A continuacion se calcula la suma de todos los digitos de . A continuacion se calcula la suma de todos los digitos de 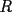 y asi sucesivamentehasta llegar a un numero de un solo digito. Encuentrelo.(Por ejemplo si tomamos y asi sucesivamentehasta llegar a un numero de un solo digito. Encuentrelo.(Por ejemplo si tomamos 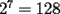 , encontramos que , encontramos que 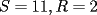 . Asi en este caso de . Asi en este caso de 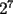 el digito buscado será 2). el digito buscado será 2).Generemos una función f, tal que para cada potencia de 2, digamos 2^n, entonces f(n) sea igual al número final obtenido según el algoritmo mostrado. Así, es fácil ver que: f(1)=2, f(2)=4, f(3)=8, f(4)=7, f(5)=5, f(6)=1 f(7)=2, f(8)=4, ... Esto nos lleva a conjeturar que el valor que toma el valor pedido sigue un ciclo, se repite con periodo 6. Es decir, f(n+6)=f(n). Demostraremos eso: Veamos que para pasar de una potencia de 2 a la siguiente, estamos multiplicando a este numero por 2, en otras palabras, multiplicamos CADA UNO DE SUS DÍGITOS por 2. Luego, la suma de sus dígitos se duplicará. Es decir, de 1 pasamos a 2, de 2 a 2*2=4, de 4 a 2*4=8, de 8 a 2*8=16-->1+6=7, 7*2=14-->1+4=5, etc...no es difícil ver cómo sigue. Entonces, como 2004 es múltiplo de 6, f(2004)=f(6)=1. Llegando al mismo resultado queThe Lord, de una manera más "humana" (realmente me sorprendió su solución Saludos, cualquier cosa me avisan Mensaje modificado por Hamon el Oct 12 2010, 06:16 PM -------------------- Empezando con Desigualdades? Encuentra aquí problemas resueltos
|
|
|
|
 Oct 12 2010, 06:39 PM Oct 12 2010, 06:39 PM
Publicado:
#7
|
|
|
Dios Matemático Supremo Grupo: Usuario FMAT Mensajes: 9.897 Registrado: 6-April 08 Miembro Nº: 19.238 Nacionalidad:  Colegio/Liceo:  Sexo:  |
que no te sorprenda la solucion de TheLord, puesto que este problema es bien conocido, sin embargo el problema original era con el numero 4444^4444.
-------------------- |
|
|
|
 Oct 12 2010, 06:44 PM Oct 12 2010, 06:44 PM
Publicado:
#8
|
|
 Dios Matemático Supremo Grupo: Team Ensayos FMAT Mensajes: 1.559 Registrado: 18-November 07 Miembro Nº: 12.754 Nacionalidad:  Sexo:  |
que no te sorprenda la solucion de TheLord, puesto que este problema es bien conocido, sin embargo el problema original era con el numero 4444^4444. Pucha, me fregaste la gracia de ese problema, que la verdad, me daba miedo resolver jaja Saludos y gracias Kaissa, igual no deja de sorprenderme este individuo Bueno, nos vemos cuando haya logrado sacar algún otro problema de esta ´prueba (de preferencia el 1 o 3 o 5) -------------------- Empezando con Desigualdades? Encuentra aquí problemas resueltos
|
|
|
|
 Oct 13 2010, 05:59 PM Oct 13 2010, 05:59 PM
Publicado:
#9
|
|
 Dios Matemático Supremo Grupo: Administrador Mensajes: 2.706 Registrado: 13-May 05 Desde: Santiago de Chile Miembro Nº: 10 Nacionalidad:  Colegio/Liceo:  Sexo:  |
estamos multiplicando a este numero por 2, en otras palabras, multiplicamos CADA UNO DE SUS DÍGITOS por 2. Este es el paso que critico de tu solución. No es exacto que cada dígito sea multiplicado por 2, debido a la "suma con reserva". Por eso es adecuado usar congruencia módulo 9, como podemos apreciar en una solución antes exhibida. En todo caso, la idea es excelente. -------------------- |
|
|
|
 Oct 13 2010, 06:33 PM Oct 13 2010, 06:33 PM
Publicado:
#10
|
|
 Dios Matemático Supremo Grupo: Team Ensayos FMAT Mensajes: 1.559 Registrado: 18-November 07 Miembro Nº: 12.754 Nacionalidad:  Sexo:  |
Este es el paso que critico de tu solución. No es exacto que cada dígito sea multiplicado por 2, debido a la "suma con reserva". Por eso es adecuado usar congruencia módulo 9, como podemos apreciar en una solución antes exhibida. En todo caso, la idea es excelente. Me corrijo: estamos multiplicando x 2 la suma de los dígitos, por lo que analizmos duplicando la suma de los dígitos, es decir, cada dígito por separado se duplica y ahi efgectuamos la nueva suma. Así evitamos el oproblema de la suma con reserva. Igual la congruencia mod 9 es mas bonita Mensaje modificado por Hamon el Oct 13 2010, 06:35 PM -------------------- Empezando con Desigualdades? Encuentra aquí problemas resueltos
|
|
|
|
  |
2 usuario(s) está(n) leyendo esta discusión (2 invitado(s) y 0 usuario(s) anónimo(s))
0 miembro(s):
| Versión Lo-Fi | Fecha y Hora actual: 2nd April 2025 - 02:42 AM |