|
|
|
|
|
|
|
  |
 May 15 2011, 06:36 PM May 15 2011, 06:36 PM
Publicado:
#91
|
|
 Dios Matemático Supremo Grupo: Usuario FMAT Mensajes: 532 Registrado: 19-October 08 Desde: Santa Cruz de la Sierra Miembro Nº: 36.531 Nacionalidad:  Sexo:  |
Uno sencillito que acabo de hacer. Sea ABC un triangulo acutangulo, P un punto dentro del triangulo y L,M,N los pies de las alturas de P sobre BC,CA,AB, respectivamente. Encuentre los puntos P (podrian haber varios) tales que BL^2+CM^2+AN^2 es minimo.
EDIT: no entiendo la solucion de pasten, dice "sea T un punto en C tal que TAB es equilatero" pero a mi parecer no existe tal punto Mensaje modificado por xD13G0x el May 15 2011, 06:43 PM -------------------- "I've never let my school interfere with my education.”
|
|
|
|
 May 15 2011, 08:11 PM May 15 2011, 08:11 PM
Publicado:
#92
|
|
 Dios Matemático Supremo Grupo: Usuario FMAT Mensajes: 765 Registrado: 6-December 05 Miembro Nº: 458 Nacionalidad:  Sexo:  |
Uno sencillito que acabo de hacer. Sea ABC un triangulo acutangulo, P un punto dentro del triangulo y L,M,N los pies de las alturas de P sobre BC,CA,AB, respectivamente. Encuentre los puntos P (podrian haber varios) tales que BL^2+CM^2+AN^2 es minimo. EDIT: no entiendo la solucion de pasten, dice "sea T un punto en C tal que TAB es equilatero" pero a mi parecer no existe tal punto Tienes razon, debi poner que el arco AB mide 120 jajaja. En todo caso hace bien calcular un poquito... -------------------- Pasten, un buen muchacho en quien confiar.
|
|
|
|
 May 21 2011, 06:38 PM May 21 2011, 06:38 PM
Publicado:
#93
|
|
 Dios Matemático Supremo Grupo: Usuario FMAT Mensajes: 532 Registrado: 19-October 08 Desde: Santa Cruz de la Sierra Miembro Nº: 36.531 Nacionalidad:  Sexo:  |
Hint: Exprese lo pedido de una forma mas "simetrica"
-------------------- "I've never let my school interfere with my education.”
|
|
|
|
 May 22 2011, 02:49 PM May 22 2011, 02:49 PM
Publicado:
#94
|
|
 Dios Matemático Supremo Grupo: Usuario FMAT Mensajes: 765 Registrado: 6-December 05 Miembro Nº: 458 Nacionalidad:  Sexo:  |
Uno sencillito que acabo de hacer. Sea ABC un triangulo acutangulo, P un punto dentro del triangulo y L,M,N los pies de las alturas de P sobre BC,CA,AB, respectivamente. Encuentre los puntos P (podrian haber varios) tales que BL^2+CM^2+AN^2 es minimo. Anduve desaparecido unos dias... aqui va la solucion: Por Pitagoras: 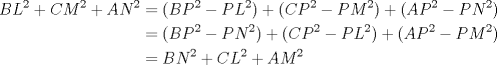 por lo tanto 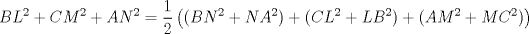 pero BN+NA, CL+LB, AM+MC son cantidades fijas (los lados del triangulo) asi que cada uno de esos tres parentesis se minimiza cuando N, L, M son puntos medios de BA, CB, AC respectivamente. Entonces P minimiza la cantidad pedida cuando es el circuncentro. Saludos. -------------------- Pasten, un buen muchacho en quien confiar.
|
|
|
|
 May 22 2011, 06:09 PM May 22 2011, 06:09 PM
Publicado:
#95
|
|
 Dios Matemático Supremo Grupo: Usuario FMAT Mensajes: 532 Registrado: 19-October 08 Desde: Santa Cruz de la Sierra Miembro Nº: 36.531 Nacionalidad:  Sexo:  |
Perfecto, ven que era sencillo?. Disculpa por no revisarlo antes.
La fuente es un shorlist de quien sabe que año xD. proponga -------------------- "I've never let my school interfere with my education.”
|
|
|
|
 May 22 2011, 08:40 PM May 22 2011, 08:40 PM
Publicado:
#96
|
|
 Dios Matemático Supremo Grupo: Usuario FMAT Mensajes: 765 Registrado: 6-December 05 Miembro Nº: 458 Nacionalidad:  Sexo:  |
El entero N es un cuadrado modulo p (es decir, un residuo cuadratico) para todo primo p. ¿Es verdad que necesariamente N tiene que ser un cuadrado?
Saludos -------------------- Pasten, un buen muchacho en quien confiar.
|
|
|
|
 May 22 2011, 09:29 PM May 22 2011, 09:29 PM
Publicado:
#97
|
|
|
Dios Matemático Supremo Grupo: Usuario FMAT Mensajes: 836 Registrado: 9-January 07 Desde: Santiasko Miembro Nº: 3.659 Nacionalidad:  Sexo:  |
Sí, necesariamente es un cuadrado. Escribamos
 la factorización prima de N y suponga que no es cuadrado, pero sí cuadrado modulo p para todo primo p, entonces alguno de los divisores primos de N debe ser impar porque de lo contrario N es potencia perfecta de 2 con exponente impar, y todas las potencias de 2 con exponente impar no son residuos cuadraticos modulo 3. Sea la factorización prima de N y suponga que no es cuadrado, pero sí cuadrado modulo p para todo primo p, entonces alguno de los divisores primos de N debe ser impar porque de lo contrario N es potencia perfecta de 2 con exponente impar, y todas las potencias de 2 con exponente impar no son residuos cuadraticos modulo 3. Sea 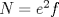 donde f es libre de cuadrados. Entonces si donde f es libre de cuadrados. Entonces si 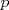 es primo, usando el símbolo de Jacobi tenemos es primo, usando el símbolo de Jacobi tenemos 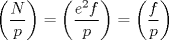 , de modo que sin perder generalidad asumo que N es libre de cuadrados. Escriba nuevamente , de modo que sin perder generalidad asumo que N es libre de cuadrados. Escriba nuevamente 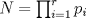 la factorizacion prima. Como N no es 2, entonces la factorizacion prima. Como N no es 2, entonces 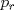 es impar. Por el teorema de Dirichlet de la existencia de infinitos primos en progresión aritmética, existe p primo tal que es impar. Por el teorema de Dirichlet de la existencia de infinitos primos en progresión aritmética, existe p primo tal que 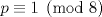 , , 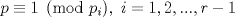 y y 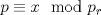 donde x es un residuo no cuadrático modulo donde x es un residuo no cuadrático modulo 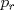 . Nuevamente usando el simbolo de Jacobi y la reciprocidad cuadratica tenemos que . Nuevamente usando el simbolo de Jacobi y la reciprocidad cuadratica tenemos que 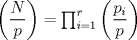 y que y que 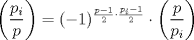 , y por las condiciones dadas sobre , y por las condiciones dadas sobre 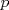 es fácil ver que es fácil ver que 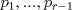 son residuos cuadraticos modulo p, pero son residuos cuadraticos modulo p, pero 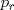 no lo es, por ende N no es residuo cuadratico modulo p, esto contradice la definicion de N. no lo es, por ende N no es residuo cuadratico modulo p, esto contradice la definicion de N.
Mensaje modificado por Felipe_ambuli el May 22 2011, 10:51 PM |
|
|
|
 May 22 2011, 11:04 PM May 22 2011, 11:04 PM
Publicado:
#98
|
|
 Dios Matemático Supremo Grupo: Usuario FMAT Mensajes: 765 Registrado: 6-December 05 Miembro Nº: 458 Nacionalidad:  Sexo:  |
Sí, necesariamente es un cuadrado. Escribamos  la factorización prima de N y suponga que no es cuadrado, pero sí cuadrado modulo p para todo primo p, entonces alguno de los divisores primos de N debe ser impar porque de lo contrario N es potencia perfecta de 2 con exponente impar, y todas las potencias de 2 con exponente impar no son residuos cuadraticos modulo 3. Sea la factorización prima de N y suponga que no es cuadrado, pero sí cuadrado modulo p para todo primo p, entonces alguno de los divisores primos de N debe ser impar porque de lo contrario N es potencia perfecta de 2 con exponente impar, y todas las potencias de 2 con exponente impar no son residuos cuadraticos modulo 3. Sea 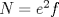 donde f es libre de cuadrados. Entonces si donde f es libre de cuadrados. Entonces si 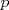 es primo, usando el símbolo de Jacobi tenemos es primo, usando el símbolo de Jacobi tenemos 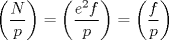 , de modo que sin perder generalidad asumo que N es libre de cuadrados. Escriba nuevamente , de modo que sin perder generalidad asumo que N es libre de cuadrados. Escriba nuevamente 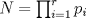 la factorizacion prima. Como N no es 2, entonces la factorizacion prima. Como N no es 2, entonces 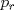 es impar. Por el teorema de Dirichlet de la existencia de infinitos primos en progresión aritmética, existe p primo tal que es impar. Por el teorema de Dirichlet de la existencia de infinitos primos en progresión aritmética, existe p primo tal que 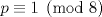 , , 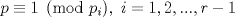 y y 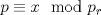 donde x es un residuo no cuadrático modulo donde x es un residuo no cuadrático modulo 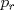 . Nuevamente usando el simbolo de Jacobi y la reciprocidad cuadratica tenemos que . Nuevamente usando el simbolo de Jacobi y la reciprocidad cuadratica tenemos que 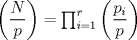 y que y que 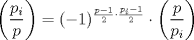 , y por las condiciones dadas sobre , y por las condiciones dadas sobre 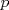 es fácil ver que es fácil ver que 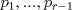 son residuos cuadraticos modulo p, pero son residuos cuadraticos modulo p, pero 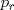 no lo es, por ende N no es residuo cuadratico modulo p, esto contradice la definicion de N. no lo es, por ende N no es residuo cuadratico modulo p, esto contradice la definicion de N.Muy bien! es mas o menos lo que tenia en mente. Si quieren averiguar mas, un buen tema para mirar es el teorema de densidad de Chebotarev. Abora propone Felipe_ambuli -------------------- Pasten, un buen muchacho en quien confiar.
|
|
|
|
 May 22 2011, 11:13 PM May 22 2011, 11:13 PM
Publicado:
#99
|
|
|
Dios Matemático Supremo Grupo: Usuario FMAT Mensajes: 836 Registrado: 9-January 07 Desde: Santiasko Miembro Nº: 3.659 Nacionalidad:  Sexo:  |
Sea A un conjunto de nueve puntos en el plano, tres a tres no colineares. Pruebe que para cada
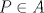 , el número de triángulos que tienen como vértices a tres de los ocho puntos restantes y que contienen a P en su interior es par. , el número de triángulos que tienen como vértices a tres de los ocho puntos restantes y que contienen a P en su interior es par.
|
|
|
|
 May 22 2011, 11:43 PM May 22 2011, 11:43 PM
Publicado:
#100
|
|
 Dios Matemático Supremo Grupo: Usuario FMAT Mensajes: 532 Registrado: 19-October 08 Desde: Santa Cruz de la Sierra Miembro Nº: 36.531 Nacionalidad:  Sexo:  |
Cambiamos 9 por un n impar.
Tomemos un cuadrilatero con vertices en A, y consideremos los 4 triangulos con vertices en los vertices del cuadrilatero, es obvio que P pertenece a 2 o a 0 de esos 4 triangulos. Si hacemos k=la cantidad de triangulos con vertices en A que contienen a P y q=una sumatoria definida asi: para cada cuadrilatero X1X2X3X4 con vertices en A, f(X1X2X3X4) donde f(X1X2X3X4) es 0 o 2 dependiendo si P pertenece a 0 o 2 triangulos con vertices en X1,X2,X3,X4, Usando lo anterior tenemos que k=q/(n-4), pues si P esta en algun triangulo con vertices en A, digamos ABC, contiene a P, entonces hay n-4 cuadrilateros (restar los vertices del triangulo y P) que cuentan el hecho que ABC contiene a P. -------------------- "I've never let my school interfere with my education.”
|
|
|
|
  |
1 usuario(s) está(n) leyendo esta discusión (1 invitado(s) y 0 usuario(s) anónimo(s))
0 miembro(s):
| Versión Lo-Fi | Fecha y Hora actual: 4th April 2025 - 02:55 PM |









