|
|
|
|
|
|
|
  |
 Jan 29 2014, 11:53 AM Jan 29 2014, 11:53 AM
Publicado:
#341
|
|
|
Dios Matemático Supremo Grupo: Usuario FMAT Mensajes: 1.116 Registrado: 12-March 11 Miembro Nº: 84.732 Nacionalidad:  Sexo:  |
Sea
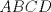 un trapecio isosceles con base mayor un trapecio isosceles con base mayor 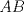 . Sus diagonales y sus lados no paralelos intersectan en . Sus diagonales y sus lados no paralelos intersectan en 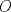 y y 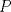 , respectivamente. Sea , respectivamente. Sea 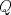 un punto sobre el circuncirculo de un punto sobre el circuncirculo de 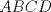 y diametralmente opuesto a y diametralmente opuesto a 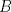 . Pruebe que la circunferencia que pasa por . Pruebe que la circunferencia que pasa por 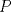 , , 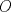 y y 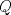 es tangente a es tangente a 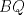 . .
Mensaje modificado por cev el Jan 29 2014, 11:56 AM -------------------- |
|
|
|
 Jan 29 2014, 04:39 PM Jan 29 2014, 04:39 PM
Publicado:
#342
|
|
 Maestro Matemático Grupo: Usuario FMAT Mensajes: 81 Registrado: 10-November 12 Miembro Nº: 112.735 Nacionalidad:  Colegio/Liceo:  Universidad: .png) Sexo:  |
Sorry por el dibujo no tengo como Mensaje modificado por asdayuyi el Jan 29 2014, 06:48 PM |
|
|
|
 Jan 29 2014, 06:35 PM Jan 29 2014, 06:35 PM
Publicado:
#343
|
|
|
Dios Matemático Supremo Grupo: Usuario FMAT Mensajes: 1.116 Registrado: 12-March 11 Miembro Nº: 84.732 Nacionalidad:  Sexo:  |
Si ya se ve para que lado vas, y esta muy bien, pero ahi tenes algun lio con la letra Q (aparentemente) porque por ej. "QA y PQ son paralelas" , "<CPQ=<QPA=<PAQ=<DBQ", "KB^2 = QK·KP" no lo veo bien, en fin revisalo todo.
-------------------- |
|
|
|
 Jan 29 2014, 06:49 PM Jan 29 2014, 06:49 PM
Publicado:
#344
|
|
 Maestro Matemático Grupo: Usuario FMAT Mensajes: 81 Registrado: 10-November 12 Miembro Nº: 112.735 Nacionalidad:  Colegio/Liceo:  Universidad: .png) Sexo:  |
ahí está editado, había confundido Q con O, ahora parece que si
|
|
|
|
 Jan 29 2014, 06:54 PM Jan 29 2014, 06:54 PM
Publicado:
#345
|
|
|
Dios Matemático Supremo Grupo: Usuario FMAT Mensajes: 1.116 Registrado: 12-March 11 Miembro Nº: 84.732 Nacionalidad:  Sexo:  |
Listo, listo, impecable che. Ahora a proponer.
-------------------- |
|
|
|
 Jan 29 2014, 07:10 PM Jan 29 2014, 07:10 PM
Publicado:
#346
|
|
 Maestro Matemático Grupo: Usuario FMAT Mensajes: 81 Registrado: 10-November 12 Miembro Nº: 112.735 Nacionalidad:  Colegio/Liceo:  Universidad: .png) Sexo:  |
Sea n un entero positivo y p un primo. Pruebe que si a,b,c son enteros tales que:
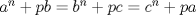 entonces a=b=c |
|
|
|
 Feb 2 2014, 09:17 PM Feb 2 2014, 09:17 PM
Publicado:
#347
|
|
 Maestro Matemático Grupo: Usuario FMAT Mensajes: 81 Registrado: 10-November 12 Miembro Nº: 112.735 Nacionalidad:  Colegio/Liceo:  Universidad: .png) Sexo:  |
Basada en la regla dos cambio el problema, para que la maratón no pierda continuidad. Otro día coloco mi solucion que ahora tengo cosas que hacer.
Las longitudes de los lados de un hexágono convexo satisfacen que AB=BC, CD=DE, EF=FA. Pruebe que 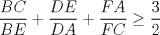 Saludosss <3 |
|
|
|
 Feb 3 2014, 04:54 AM Feb 3 2014, 04:54 AM
Publicado:
#348
|
|
 Doctor en Matemáticas Grupo: Colaborador Silver Mensajes: 193 Registrado: 17-August 12 Desde: Loncuma :3 Miembro Nº: 110.077 Nacionalidad:  Sexo:  |
Hola bb <3
Besitos para ti :** |
|
|
|
 Feb 3 2014, 09:49 AM Feb 3 2014, 09:49 AM
Publicado:
#349
|
|
 Maestro Matemático Grupo: Usuario FMAT Mensajes: 81 Registrado: 10-November 12 Miembro Nº: 112.735 Nacionalidad:  Colegio/Liceo:  Universidad: .png) Sexo:  |
Correcto
Proponga :3 |
|
|
|
 Feb 3 2014, 01:07 PM Feb 3 2014, 01:07 PM
Publicado:
#350
|
|
 Doctor en Matemáticas Grupo: Colaborador Silver Mensajes: 193 Registrado: 17-August 12 Desde: Loncuma :3 Miembro Nº: 110.077 Nacionalidad:  Sexo:  |
Gracias :3
Sea 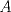 el subconjunto de numeros enteros que cumple las siguientes condiciones: el subconjunto de numeros enteros que cumple las siguientes condiciones: 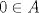  Si Si 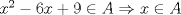  Si Si 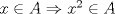 Demuestre que: 1. Existen 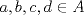 no nulos, tales que no nulos, tales que 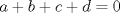 2. 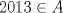
|
|
|
|
  |
1 usuario(s) está(n) leyendo esta discusión (1 invitado(s) y 0 usuario(s) anónimo(s))
0 miembro(s):
| Versión Lo-Fi | Fecha y Hora actual: 8th July 2025 - 01:46 AM |












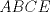 tenemos:
tenemos: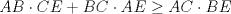 , pero
, pero 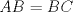 , sacando factor comun y dividiendo por
, sacando factor comun y dividiendo por 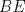 se tiene
se tiene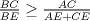
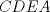 y
y 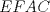 se desprende:
se desprende: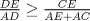 y
y 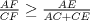
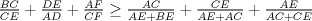 , de esto lo pedido es directo, ya que la ultima desigualdad es la de Nesbitt.
, de esto lo pedido es directo, ya que la ultima desigualdad es la de Nesbitt.