|
|
|
|
|
|
|
  |
 Jul 15 2013, 01:00 AM Jul 15 2013, 01:00 AM
Publicado:
#241
|
|
 Dios Matemático Grupo: Moderador Mensajes: 269 Registrado: 30-August 10 Desde: Santiago, Chile Miembro Nº: 76.269 Nacionalidad:  Colegio/Liceo:  Universidad:  Sexo:  |
Good solution, propones
Saludos =)!!! -------------------- Estudiante Instituto Nacional General José Miguel Carrera IV Medio(2013) 17 años. Estaba Jesús predicando en el monte Sinaí y dijo a sus discípulos: y = ax² + bx + c ¿Y eso qué es? Dijo uno de los discípulos. A lo que Jesús respondió: ¡Una parábola !  |
|
|
|
 Jul 15 2013, 01:15 AM Jul 15 2013, 01:15 AM
Publicado:
#242
|
|
 Dios Matemático Grupo: Usuario FMAT Mensajes: 217 Registrado: 5-April 11 Desde: no se :c Miembro Nº: 86.300 Nacionalidad:  Colegio/Liceo:  Sexo:  |
Sea n>1 un natural y p primo tales que p|n3-1 y n|p-1. Demuestre que 4p-3 es un cuadrado perfecto.
-------------------- Cuando eliminamos lo imposible lo que queda, por improbable que parezca...siempre será la verdad...
Nada tiene sentido, pero todo tiene significado. |
|
|
|
 Jul 15 2013, 12:11 PM Jul 15 2013, 12:11 PM
Publicado:
#243
|
|
|
Dios Matemático Supremo Grupo: Usuario FMAT Mensajes: 9.897 Registrado: 6-April 08 Miembro Nº: 19.238 Nacionalidad:  Colegio/Liceo:  Sexo:  |
Solución:
Mensaje modificado por Kaissa el Jul 15 2013, 12:13 PM -------------------- |
|
|
|
 Jul 15 2013, 12:34 PM Jul 15 2013, 12:34 PM
Publicado:
#244
|
|
 Dios Matemático Grupo: Usuario FMAT Mensajes: 233 Registrado: 21-February 12 Desde: Cerro Navia, Santiago - Valparaíso Miembro Nº: 101.376 Nacionalidad:  Colegio/Liceo:  Universidad:  Sexo:  |
Creo que tengo una más corta
Solución: Saludos! --------------------  |
|
|
|
 Jul 15 2013, 01:09 PM Jul 15 2013, 01:09 PM
Publicado:
#245
|
|
 Dios Matemático Grupo: Moderador Mensajes: 269 Registrado: 30-August 10 Desde: Santiago, Chile Miembro Nº: 76.269 Nacionalidad:  Colegio/Liceo:  Universidad:  Sexo:  |
Creo que tengo una más corta Solución: Saludos! Acuerdate que si a|b entonces |a| es menor o igual que |b|. Ahí asumes directamente que n^2 es menor que p-1, lo cual no es del todo cierto asumirlo al tiro. Saludos. Mensaje modificado por Seba² el Jul 15 2013, 01:10 PM -------------------- Estudiante Instituto Nacional General José Miguel Carrera IV Medio(2013) 17 años. Estaba Jesús predicando en el monte Sinaí y dijo a sus discípulos: y = ax² + bx + c ¿Y eso qué es? Dijo uno de los discípulos. A lo que Jesús respondió: ¡Una parábola !  |
|
|
|
 Jul 15 2013, 02:15 PM Jul 15 2013, 02:15 PM
Publicado:
#246
|
|
 Dios Matemático Grupo: Usuario FMAT Mensajes: 217 Registrado: 5-April 11 Desde: no se :c Miembro Nº: 86.300 Nacionalidad:  Colegio/Liceo:  Sexo:  |
Correcto Kaissa, propones!
-------------------- Cuando eliminamos lo imposible lo que queda, por improbable que parezca...siempre será la verdad...
Nada tiene sentido, pero todo tiene significado. |
|
|
|
 Jul 15 2013, 02:58 PM Jul 15 2013, 02:58 PM
Publicado:
#247
|
|
|
Dios Matemático Supremo Grupo: Usuario FMAT Mensajes: 9.897 Registrado: 6-April 08 Miembro Nº: 19.238 Nacionalidad:  Colegio/Liceo:  Sexo:  |

-------------------- |
|
|
|
 Jul 15 2013, 07:37 PM Jul 15 2013, 07:37 PM
Publicado:
#248
|
|
 Dios Matemático Supremo Grupo: Usuario FMAT Mensajes: 688 Registrado: 8-November 09 Desde: Villarrica Miembro Nº: 61.657 Nacionalidad:  Colegio/Liceo:  Universidad: .png) Sexo:  |
Too easy!
Sean x,y,z los ángulos en A, B, C, respectivamente. Tenemos que A'BC=90-x, A'CB=90-y, A'BA=2x-90 y A'CA=2y-90. Ahora por Ceva trigonométrico aplicado al punto A' tenemos (sen(BAA')/sen(A'AC))=(sen(90-y)/sen(2y-90))(sen(2x-90)/sen(90-x)), análogamente concluimos para los demás casos, de donde es fácil ver que (sen(BAA')/sen(A'AC))(sen(ACC')/sen(C'CB))(sen(CBB')/sen(B'BA))=1 luego por el recíproco de Ceva trigonométrico finalizamos. Saludos. -------------------- yo no soy especial
a pesar que ella lo dijo tengo unos krk y un celular hechizo aún vácilo SFDK en el segundo piso y la frase final da igual la improviso |
|
|
|
 Jul 15 2013, 09:41 PM Jul 15 2013, 09:41 PM
Publicado:
#249
|
|
|
Dios Matemático Supremo Grupo: Usuario FMAT Mensajes: 9.897 Registrado: 6-April 08 Miembro Nº: 19.238 Nacionalidad:  Colegio/Liceo:  Sexo:  |
Buena solución!
Te comparto la geométrica: PD: ¬¬ Propón (me intriga ver qué tendrás en mente) -------------------- |
|
|
|
 Jul 15 2013, 10:34 PM Jul 15 2013, 10:34 PM
Publicado:
#250
|
|
 Dios Matemático Supremo Grupo: Usuario FMAT Mensajes: 688 Registrado: 8-November 09 Desde: Villarrica Miembro Nº: 61.657 Nacionalidad:  Colegio/Liceo:  Universidad: .png) Sexo:  |
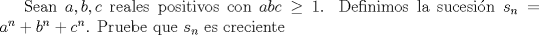 Saludos PD: Si el problema en cuestión no le parece lo suficientemente interesante podría tratar de extenderlo. Propongo una extensión tomando m reales positivos 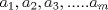 , con producto , con producto 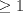 y y 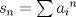 , igualmente afirmo en éste caso que la sucesión es creciente. Ojalá se les ocurra algo mas lindo. , igualmente afirmo en éste caso que la sucesión es creciente. Ojalá se les ocurra algo mas lindo.
Mensaje modificado por Pedantic Anarchy el Jul 16 2013, 12:05 AM -------------------- yo no soy especial
a pesar que ella lo dijo tengo unos krk y un celular hechizo aún vácilo SFDK en el segundo piso y la frase final da igual la improviso |
|
|
|
  |
2 usuario(s) está(n) leyendo esta discusión (2 invitado(s) y 0 usuario(s) anónimo(s))
0 miembro(s):
| Versión Lo-Fi | Fecha y Hora actual: 12th September 2025 - 10:33 PM |












![TEX: \[p\mid (n-1)(n^{2}+n+1)\]<br />](/tex-image/94dba1265919b1ea291a9a8c531bba13.png) . Por la segundo hipótesis, notamos que
. Por la segundo hipótesis, notamos que 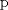 no divide a
no divide a 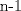 ; puesto que
; puesto que 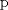 es primo entonces ambos son coprimos; se sigue que
es primo entonces ambos son coprimos; se sigue que ![TEX: \[p\mid (n^{2}+n+1)\rightarrow p\leq n^{2}+n+1\]<br />](/tex-image/a8989625ba4b4971cf13fe4a73bceceb.png) . Como
. Como ![TEX: \[n\mid p-1\rightarrow n\mid p-1-n^{2}\]<br />](/tex-image/a506d61fafad85ccd7a00f5bbd252203.png) entonces
entonces ![TEX: \[n^{2}+n+1\leq p\]<br />](/tex-image/3c80b216cd0683e7d50177e45848fc63.png) . De aquí se sigue que
. De aquí se sigue que ![TEX: \[p=n^{2}+n+1\]<br />](/tex-image/13f505d82466b0a68046913e1ae77e6c.png) entonces multiplicando por 4 y restando 3 tenemos que
entonces multiplicando por 4 y restando 3 tenemos que ![TEX: \[4p-3=(2n+1)^{2}\]<br />](/tex-image/634301e55c9a868dae75e5f12c8fdd0f.png) , que en efecto, es un cuadrado perfecto.
, que en efecto, es un cuadrado perfecto.