|
|
|
|
|
|
|
  |
 Apr 28 2011, 08:22 PM Apr 28 2011, 08:22 PM
Publicado:
#21
|
|
 Dios Matemático Supremo Grupo: Usuario FMAT Mensajes: 532 Registrado: 19-October 08 Desde: Santa Cruz de la Sierra Miembro Nº: 36.531 Nacionalidad:  Sexo:  |
Pasten, ya pasaron 24 horas y nadie resolvio el problema, kisas deberias cambiarlo por otro, este esta medio rarito
-------------------- "I've never let my school interfere with my education.”
|
|
|
|
 Apr 28 2011, 08:53 PM Apr 28 2011, 08:53 PM
Publicado:
#22
|
|
 Dios Matemático Supremo Grupo: Usuario FMAT Mensajes: 765 Registrado: 6-December 05 Miembro Nº: 458 Nacionalidad:  Sexo:  |
Pasten, ya pasaron 24 horas y nadie resolvio el problema, kisas deberias cambiarlo por otro, este esta medio rarito Ok. Ahora estoy cocinando asi que no puedo estar por mucho rato en el PC. Les dejo el nuevo propuesto, y en algo asi como unahora posteo la solucion del que no resulto. NUEVO PROPUESTO: Tenemos un tablero cuadrado de N casilleros por lado. Encuentre los N para los cuales es posible hacer lo siguiente: Ubicar una ficha en el tablero (a voluntad, donde quieran), moverla de a un casillero a otro pero solo a casilleros que comparten un lado con el anterior, y de esta forma recorrer todo el tablero sin pasar 2 veces por el mismo sitio, terminando en un casillero contiguo al inicial (o sea, casillero inicial y final deben compartir un lado). Ademas, para aquellos N donde no se pueda, indicar cual es el numero minimo de veces que es necesario pasar de nuevo por un casillero que ya se ha visitado, con la finalidad de recorrer todo el tablero y acabar en un casillero contiguo al inicial. Saludos! -------------------- Para todos los que se preguntan "que estara cocinando Pasten?" la respuesta es: arroz con tomate y pescado frito apanado. Mensaje modificado por Pasten el Apr 28 2011, 09:08 PM -------------------- Pasten, un buen muchacho en quien confiar.
|
|
|
|
 Apr 28 2011, 09:40 PM Apr 28 2011, 09:40 PM
Publicado:
#23
|
|
 Dios Matemático Supremo Grupo: Usuario FMAT Mensajes: 532 Registrado: 19-October 08 Desde: Santa Cruz de la Sierra Miembro Nº: 36.531 Nacionalidad:  Sexo:  |
Vamos a ubicar los puntos como pares ordenados (i,j) con 1<=i,j<=2k. Voy a poner (a,b)->(c,d) para indicar que la ficha se mueve de (a,b) a (c,d) y (a,b)->...-> para indicar que la ficha se mueve de (a,b) a (c,d) en linea recta.
Para todos los n par se puede hacer eso. Con estos movimientos se obtiene lo pedid (1,1)->...->(1,n)->...->(n,n)->(n,n-1)->...->(2,n-1)->(2,n-2)->(n,n-2)-> (asi sucesivamente) ->(n,2)->(n,1)->(2,1). Ahora si n es impar , coloreamos el tablero de blanco y negro como en ajedrez, con mas casillas negras que blancas. Cuando la ficha se mueve, pasa de una casilla negra a una blanca o de una blanca a una negra, asi que la ficha debe empezar en una casilla negra y luego termina tambien en una casilla negra, osea no termina en una casilla contigua a la inicial (pues la inicial es negra y las casillas contiguas a las negras son blancas). Pero ahora veamos que pasando una sola vez de nuevo por una casilla, se puede lograr lo pedido en un tablero de lado impar. Lo hacemos con los siguientes movimientos (1,1)->...->(1,n)->...->(n,n)->(n,n-1)->...->(2,n-1)->(2,n-2)->(n,n-2)-> (asi sucesivamente) ->(n,3)->(n,2)->(n,1)->(n-1,1)->(n-1,2)->(n-2,2)->(n-2,1)-> (asi sucesivamente) ->(2,1)->(2,2)->(1,2). Mensaje modificado por xD13G0x el Apr 28 2011, 09:44 PM -------------------- "I've never let my school interfere with my education.”
|
|
|
|
 Apr 28 2011, 10:00 PM Apr 28 2011, 10:00 PM
Publicado:
#24
|
|
 Dios Matemático Supremo Grupo: Usuario FMAT Mensajes: 765 Registrado: 6-December 05 Miembro Nº: 458 Nacionalidad:  Sexo:  |
Solucion del propuesto anterior:
parte 1: NO parte 2: SI Explicare la parte 1. Para la parte 2 hay que dar un ejemplo, y para eso hay que dejar una caja dentro de otra en un posicion complicada de explicar sin dibujos ni calculos trigonometricos desagradables, asi que no lo pasare a LaTeX ni lo posteare (pero se puede!). Demostracion de que la repsuesta de la parte 1 es "NO": Digamos que queremos guardar un bulto B de aristas x,y,z, dentro de una encomienda E de aristas u,v,w. Por definicion de bulto y encomienda se tiene 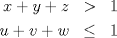 Queremos demostrar que en realidad no es posible guardar B dentro de E. Para esto usaremos una construccion auxiliar. Para t>0 definimos S(t) como el conjunto de puntos del espacio que estan a distancia menor o igual que t del bulto B (el interior de B cuenta como parte de B). Definimos tambien R(t) como el conjunto de puntos del espacio que estan a distancia menor o igual que t de la encomienda E (el interior de E cuenta como parte de E). Por contradiccion, supongamos que es posible guardar B dentro de E. [1.] S(t) esta incluido en R(t) para cada t>0. En efecto, si un punto P del espacio esta a distancia d de B con d menor o igual que t, entonces consideramos L el segmento mas corto de P a B. Se cumple que, o bien P esta en el interior de E (en cuyo caso P esta en R(t)) o bien L corta la superficie de E y por ende P esta a distancia menor que d (luego, menor que t) de la encomienda E (en este caso tambien P esta en R(t)). Ahora, queremos estudiar el volumen de R(t) y S(t). Por [1.] ya sabemos que: [2.] V(S(t)) es menor o igual que V(R(t)) para todo t>0, donde V denota el volumen (porque uno esta incluido en el otro asi que su volumen es menor o igual). Esto es correcto, pero queremos informacion mas detallada. Para esto vamos a descomponer R(t) y S(t) en partes mas pequeñas que guardan informacion de E y B. Veamos primero el caso de E. R(t) admite la siguiente descomposicion: Primero, E esta siempre dentro de R(t). Ahora, sobre cada cara de E construimos un paralelepipedo de base esa cara y altura t. Aun no completamos R(t), quedan espacios sobre las aristas y los vertices. Sobre las aristas ponemos cuartos de cilindros, cuya altura es la arista respectiva y el radio es t. Finalmente en cada vertice ponemos lo que falta para completar R(t), esto es, un octavo de esfera de radio t en cada vertice (hacer un dibujito de esta descomposicion les puede ayudar). Un momento de reflexion nos muestra que efectivamente estas piezas forman una descomposicion de R(t) sin olvidar ni repetir nada. [3.] Entonces, recordando que las aristas son u,v,w, obtenemos la siguiente formula para el volumen de R(t): 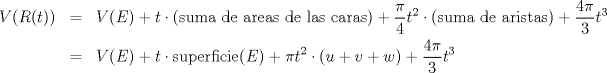 [4.] Similarmente, para B que tiene aristas x,y,z obtenemos la siguiente formula 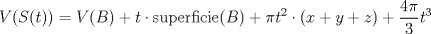 Finalmente, de [2.], [3.], [4.] obtenemos 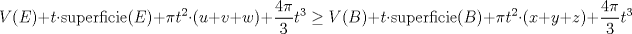 lo que nos da: 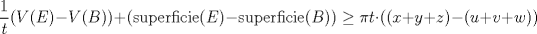 Observe que el lado izquierdo permanece acotado a medida que t es cada vez mas grande, asi que el lado derecho permanece acotado superiormente cuando t se hace mas grande. Pero (x+y+z)-(u+v+w)>0 porque B es bulto y E es encomienda. Contradiccion. Saludos Mensaje modificado por Pasten el Apr 28 2011, 10:01 PM -------------------- Pasten, un buen muchacho en quien confiar.
|
|
|
|
 Apr 28 2011, 10:14 PM Apr 28 2011, 10:14 PM
Publicado:
#25
|
|
 Dios Matemático Supremo Grupo: Usuario FMAT Mensajes: 765 Registrado: 6-December 05 Miembro Nº: 458 Nacionalidad:  Sexo:  |
Vamos a ubicar los puntos como pares ordenados (i,j) con 1<=i,j<=2k. Voy a poner (a,b)->(c,d) para indicar que la ficha se mueve de (a,b) a (c,d) y (a,b)->...-> para indicar que la ficha se mueve de (a,b) a (c,d) en linea recta. Para todos los n par se puede hacer eso. Con estos movimientos se obtiene lo pedid (1,1)->...->(1,n)->...->(n,n)->(n,n-1)->...->(2,n-1)->(2,n-2)->(n,n-2)-> (asi sucesivamente) ->(n,2)->(n,1)->(2,1). Ahora si n es impar , coloreamos el tablero de blanco y negro como en ajedrez, con mas casillas negras que blancas. Cuando la ficha se mueve, pasa de una casilla negra a una blanca o de una blanca a una negra, asi que la ficha debe empezar en una casilla negra y luego termina tambien en una casilla negra, osea no termina en una casilla contigua a la inicial (pues la inicial es negra y las casillas contiguas a las negras son blancas). Pero ahora veamos que pasando una sola vez de nuevo por una casilla, se puede lograr lo pedido en un tablero de lado impar. Lo hacemos con los siguientes movimientos (1,1)->...->(1,n)->...->(n,n)->(n,n-1)->...->(2,n-1)->(2,n-2)->(n,n-2)-> (asi sucesivamente) ->(n,3)->(n,2)->(n,1)->(n-1,1)->(n-1,2)->(n-2,2)->(n-2,1)-> (asi sucesivamente) ->(2,1)->(2,2)->(1,2). Correcto! Fuente: esta es la parte obvia de la pregunta 3 de la ibero 2006. Ahora xD13G0x propone. Saludos! -------------------- Pasten, un buen muchacho en quien confiar.
|
|
|
|
 Apr 28 2011, 10:24 PM Apr 28 2011, 10:24 PM
Publicado:
#26
|
|
 Dios Matemático Supremo Grupo: Usuario FMAT Mensajes: 532 Registrado: 19-October 08 Desde: Santa Cruz de la Sierra Miembro Nº: 36.531 Nacionalidad:  Sexo:  |
Sea
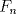 el n-esimo numero de fibonacci. Pruebe que si el n-esimo numero de fibonacci. Pruebe que si 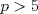 es un primo entonces es un primo entonces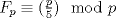 Donde 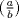 es el simbolo de legendre. es el simbolo de legendre.
Mensaje modificado por xD13G0x el Apr 28 2011, 10:24 PM -------------------- "I've never let my school interfere with my education.”
|
|
|
|
 Apr 29 2011, 12:22 AM Apr 29 2011, 12:22 AM
Publicado:
#27
|
|
 Dios Matemático Supremo Grupo: Usuario FMAT Mensajes: 765 Registrado: 6-December 05 Miembro Nº: 458 Nacionalidad:  Sexo:  |
Sea 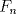 el n-esimo numero de fibonacci. Pruebe que si el n-esimo numero de fibonacci. Pruebe que si 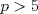 es un primo entonces es un primo entonces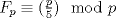 Donde 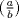 es el simbolo de legendre. es el simbolo de legendre.Debo decir que dude en postear una solucion porque la usuaria Kamelot me dijo que deje participar a mas gente, y porque no seria justo en este problema en particular. Entonces lo que hare sera poner una solucion no-olimpica (unicamente porque es muy corta y simple!) y asi dejo que la gente siga buscando alguna solucion adecuada al nivel de la discusion. Antes de proceder con la demostracion, quiero hacer notar que la formula de Binet para la recurrencia de Fibonacci es cierta sobre cualquier campo de caracteristica distinta de 2 o 5 (por ejemplo, la demostracion por valores propios, o por induccion, funcionan en cualquier campo de caracteristica distinta de 2 y 5). Hecha esta aclaracion, vamos con la demostracion:  Saludos -------------------- Pasten, un buen muchacho en quien confiar.
|
|
|
|
 Apr 29 2011, 10:12 PM Apr 29 2011, 10:12 PM
Publicado:
#28
|
|
 Dios Matemático Supremo Grupo: Usuario FMAT Mensajes: 688 Registrado: 8-November 09 Desde: Villarrica Miembro Nº: 61.657 Nacionalidad:  Colegio/Liceo:  Universidad: .png) Sexo:  |
Sea 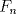 el n-esimo numero de fibonacci. Pruebe que si el n-esimo numero de fibonacci. Pruebe que si 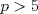 es un primo entonces es un primo entonces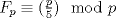 Donde 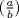 es el simbolo de legendre. es el simbolo de legendre.
Mensaje modificado por Pedantic Anarchy el May 1 2011, 08:40 PM -------------------- yo no soy especial
a pesar que ella lo dijo tengo unos krk y un celular hechizo aún vácilo SFDK en el segundo piso y la frase final da igual la improviso |
|
|
|
 Apr 29 2011, 10:54 PM Apr 29 2011, 10:54 PM
Publicado:
#29
|
|
 Dios Matemático Supremo Grupo: Usuario FMAT Mensajes: 532 Registrado: 19-October 08 Desde: Santa Cruz de la Sierra Miembro Nº: 36.531 Nacionalidad:  Sexo:  |
solucion correcta. proponga su ***.
(no tengo fuente xd) -------------------- "I've never let my school interfere with my education.”
|
|
|
|
 Apr 29 2011, 11:00 PM Apr 29 2011, 11:00 PM
Publicado:
#30
|
|
 Dios Matemático Supremo Grupo: Usuario FMAT Mensajes: 688 Registrado: 8-November 09 Desde: Villarrica Miembro Nº: 61.657 Nacionalidad:  Colegio/Liceo:  Universidad: .png) Sexo:  |
Sean O,H el circuncentro y ortocentro del triangulo ABC, respectivamente. Llamemos M,N a los puntos medios de BH y CH, respectivamente. Defina B´ como el punto diametralmente opuesto con B, respecto al circuncirculo del ABC. Pruebe que si HONM es un cuadrilatero ciclico, entonces B´N=AC/2
-------------------- yo no soy especial
a pesar que ella lo dijo tengo unos krk y un celular hechizo aún vácilo SFDK en el segundo piso y la frase final da igual la improviso |
|
|
|
  |
1 usuario(s) está(n) leyendo esta discusión (1 invitado(s) y 0 usuario(s) anónimo(s))
0 miembro(s):
| Versión Lo-Fi | Fecha y Hora actual: 20th October 2025 - 09:28 PM |









