|
|
|
|
|
|
|
  |
 Dec 23 2011, 03:32 PM Dec 23 2011, 03:32 PM
Publicado:
#151
|
|
 Dios Matemático Supremo Grupo: Usuario FMAT Mensajes: 532 Registrado: 19-October 08 Desde: Santa Cruz de la Sierra Miembro Nº: 36.531 Nacionalidad:  Sexo:  |
A pedido de un ** voy a cambiar el problema:
Determine la paridad de la cantidad de tuplas 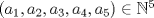 satisfaciendo satisfaciendo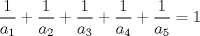
Mensaje modificado por xD13G0x el Dec 26 2011, 11:04 AM -------------------- "I've never let my school interfere with my education.”
|
|
|
|
 Dec 24 2011, 06:50 PM Dec 24 2011, 06:50 PM
Publicado:
#152
|
|
 Dios Matemático Supremo Grupo: Usuario FMAT Mensajes: 688 Registrado: 8-November 09 Desde: Villarrica Miembro Nº: 61.657 Nacionalidad:  Colegio/Liceo:  Universidad: .png) Sexo:  |
 Edit: Este Diego que me hace equivocarme xd Mensaje modificado por Pedantic Anarchy el Dec 26 2011, 12:19 PM -------------------- yo no soy especial
a pesar que ella lo dijo tengo unos krk y un celular hechizo aún vácilo SFDK en el segundo piso y la frase final da igual la improviso |
|
|
|
 Dec 25 2011, 11:51 AM Dec 25 2011, 11:51 AM
Publicado:
#153
|
|
 Dios Matemático Supremo Grupo: Administrador Mensajes: 2.706 Registrado: 13-May 05 Desde: Santiago de Chile Miembro Nº: 10 Nacionalidad:  Colegio/Liceo:  Sexo:  |
A pedido de un ** voy a cambiar el problema: Determine la paridad de la cantidad de tuplas 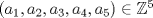 satisfaciendo satisfaciendo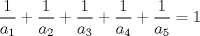 (3,3,3,n,-n) es solución para todo entero positivo n, entonces tiene infinitas soluciones. ¿Seguro que son soluciones en 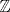 ? ?
-------------------- |
|
|
|
 Dec 26 2011, 09:40 AM Dec 26 2011, 09:40 AM
Publicado:
#154
|
|
 Dios Matemático Supremo Grupo: Usuario FMAT Mensajes: 532 Registrado: 19-October 08 Desde: Santa Cruz de la Sierra Miembro Nº: 36.531 Nacionalidad:  Sexo:  |
(3,3,3,n,-n) es solución para todo entero positivo n, entonces tiene infinitas soluciones. ¿Seguro que son soluciones en 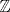 ? ?aaaaaaa, lindia pifia me mande xd, ahora que lo veo debe ser N. -------------------- "I've never let my school interfere with my education.”
|
|
|
|
 Dec 26 2011, 11:10 AM Dec 26 2011, 11:10 AM
Publicado:
#155
|
|
 Dios Matemático Supremo Grupo: Usuario FMAT Mensajes: 532 Registrado: 19-October 08 Desde: Santa Cruz de la Sierra Miembro Nº: 36.531 Nacionalidad:  Sexo:  |
Correcto en cualquier caso pedantic
-------------------- "I've never let my school interfere with my education.”
|
|
|
|
 Dec 26 2011, 12:02 PM Dec 26 2011, 12:02 PM
Publicado:
#156
|
|
 Dios Matemático Supremo Grupo: Usuario FMAT Mensajes: 688 Registrado: 8-November 09 Desde: Villarrica Miembro Nº: 61.657 Nacionalidad:  Colegio/Liceo:  Universidad: .png) Sexo:  |
En un triangulo agudo ABC, es dado que 2AB=AC+BC .Pruebe que el incentro del triangulo, el circumcentro del triangulo, el punto medio de CA y el punto medio de CB son conciclicos.
-------------------- yo no soy especial
a pesar que ella lo dijo tengo unos krk y un celular hechizo aún vácilo SFDK en el segundo piso y la frase final da igual la improviso |
|
|
|
 Jan 7 2012, 07:57 PM Jan 7 2012, 07:57 PM
Publicado:
#157
|
|
 Dios Matemático Supremo Grupo: Usuario FMAT Mensajes: 532 Registrado: 19-October 08 Desde: Santa Cruz de la Sierra Miembro Nº: 36.531 Nacionalidad:  Sexo:  |
Sea
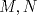 los puntos medios de los puntos medios de 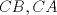 respectivamente y respectivamente y 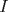 el incentro. Sea el incentro. Sea 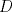 en en 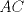 tal que tal que 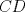 es bisectriz. Tenemos que es bisectriz. Tenemos que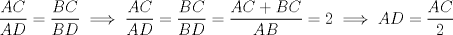 . Como . Como 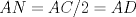 y y 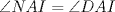 , los triangulos , los triangulos 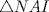 y y 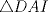 son iguales. Asi son iguales. Asi 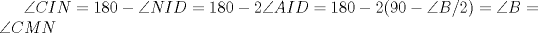 de donde 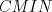 es ciclico y la conclusion es trivial. es ciclico y la conclusion es trivial.
Mensaje modificado por xD13G0x el Jan 7 2012, 07:59 PM -------------------- "I've never let my school interfere with my education.”
|
|
|
|
 Jan 7 2012, 08:11 PM Jan 7 2012, 08:11 PM
Publicado:
#158
|
|
 Dios Matemático Supremo Grupo: Usuario FMAT Mensajes: 688 Registrado: 8-November 09 Desde: Villarrica Miembro Nº: 61.657 Nacionalidad:  Colegio/Liceo:  Universidad: .png) Sexo:  |
Sea 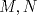 los puntos medios de los puntos medios de 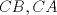 respectivamente y respectivamente y 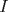 el incentro. Sea el incentro. Sea 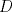 en en 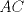 tal que tal que 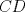 es bisectriz. Tenemos que es bisectriz. Tenemos que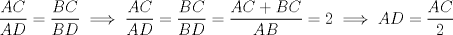 . Como . Como 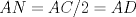 y y 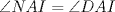 , los triangulos , los triangulos 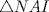 y y 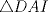 son iguales. Asi son iguales. Asi 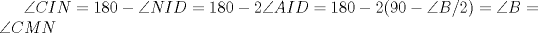 de donde 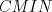 es ciclico y la conclusion es trivial. es ciclico y la conclusion es trivial.Correcto. -------------------- yo no soy especial
a pesar que ella lo dijo tengo unos krk y un celular hechizo aún vácilo SFDK en el segundo piso y la frase final da igual la improviso |
|
|
|
 Jan 7 2012, 08:13 PM Jan 7 2012, 08:13 PM
Publicado:
#159
|
|
 Dios Matemático Supremo Grupo: Usuario FMAT Mensajes: 532 Registrado: 19-October 08 Desde: Santa Cruz de la Sierra Miembro Nº: 36.531 Nacionalidad:  Sexo:  |
Demuestre que:
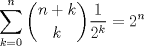
-------------------- "I've never let my school interfere with my education.”
|
|
|
|
 Jan 22 2012, 11:51 PM Jan 22 2012, 11:51 PM
Publicado:
#160
|
|
|
Dios Matemático Grupo: Usuario FMAT Mensajes: 206 Registrado: 25-January 11 Miembro Nº: 83.389 |
|
|
|
|
  |
1 usuario(s) está(n) leyendo esta discusión (1 invitado(s) y 0 usuario(s) anónimo(s))
0 miembro(s):
| Versión Lo-Fi | Fecha y Hora actual: 25th April 2025 - 11:54 PM |









