|
|
|
|
|
|
|
  |
 Jul 9 2011, 08:41 PM Jul 9 2011, 08:41 PM
Publicado:
#131
|
|
 Dios Matemático Supremo Grupo: Usuario FMAT Mensajes: 532 Registrado: 19-October 08 Desde: Santa Cruz de la Sierra Miembro Nº: 36.531 Nacionalidad:  Sexo:  |
Sea
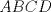 un trapecio con un trapecio con 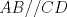 y y 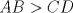 . . 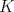 y y 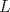 son puntos en son puntos en 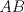 y y 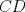 , respectivamente, tales que , respectivamente, tales que 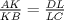 . Suponga que hay puntos . Suponga que hay puntos 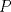 y y 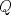 en el segmento en el segmento 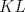 tales que tales que 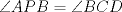 y y 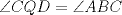 . Pruebe que . Pruebe que 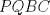 es ciclico. es ciclico.
-------------------- "I've never let my school interfere with my education.”
|
|
|
|
 Jul 10 2011, 10:45 PM Jul 10 2011, 10:45 PM
Publicado:
#132
|
|
 Dios Matemático Supremo Grupo: Usuario FMAT Mensajes: 688 Registrado: 8-November 09 Desde: Villarrica Miembro Nº: 61.657 Nacionalidad:  Colegio/Liceo:  Universidad: .png) Sexo:  |
A raíz de la razones dadas en el enunciado es trivial que DA,CB y KL concurren, llamemos al punto de concurrencia X. Sea Q´ el punto de intersección de las paralelas a DQ por A y a QC por B, como los triángulos DQC y AQ´B son homoieticos tenemos que X,Q,P y Q´ viven en la recta KL. También 180=DCB+CBA=APB+DQC=APB+AQ´B, de donde el cuadrilátero AQ´BP es cíclico, ademas como XBA=AQ´B se tiene que XB es tangente al circumcirculo del AQ´BP y por ende XBP=XQ´B=XQC lo que implica que XBP=XQC de donde se concluye que el BQPC es cíclico, demostrando lo pedido.
Mensaje modificado por Pedantic Anarchy el Jul 11 2011, 11:41 AM -------------------- yo no soy especial
a pesar que ella lo dijo tengo unos krk y un celular hechizo aún vácilo SFDK en el segundo piso y la frase final da igual la improviso |
|
|
|
 Jul 10 2011, 10:46 PM Jul 10 2011, 10:46 PM
Publicado:
#133
|
|
 Dios Matemático Supremo Grupo: Usuario FMAT Mensajes: 532 Registrado: 19-October 08 Desde: Santa Cruz de la Sierra Miembro Nº: 36.531 Nacionalidad:  Sexo:  |
Correcta su ***, el problema es de una imo de cierto año xd. Proponga
-------------------- "I've never let my school interfere with my education.”
|
|
|
|
 Jul 10 2011, 10:59 PM Jul 10 2011, 10:59 PM
Publicado:
#134
|
|
 Dios Matemático Supremo Grupo: Usuario FMAT Mensajes: 688 Registrado: 8-November 09 Desde: Villarrica Miembro Nº: 61.657 Nacionalidad:  Colegio/Liceo:  Universidad: .png) Sexo:  |
Demuestre que la ecuacion diofantica
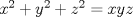 tiene infinitas soluciones enteras. tiene infinitas soluciones enteras.
Mensaje modificado por Pedantic Anarchy el Jul 10 2011, 11:00 PM -------------------- yo no soy especial
a pesar que ella lo dijo tengo unos krk y un celular hechizo aún vácilo SFDK en el segundo piso y la frase final da igual la improviso |
|
|
|
 Jul 10 2011, 11:30 PM Jul 10 2011, 11:30 PM
Publicado:
#135
|
|
 Dios Matemático Supremo Grupo: Usuario FMAT Mensajes: 532 Registrado: 19-October 08 Desde: Santa Cruz de la Sierra Miembro Nº: 36.531 Nacionalidad:  Sexo:  |
Too mainstream.
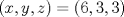 es solucion. Supongamos que tenemos una solucion es solucion. Supongamos que tenemos una solucion 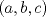 con con 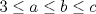 . Tenemos . Tenemos 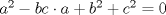 , viendo esa ecuacion como cuadratica en , viendo esa ecuacion como cuadratica en  , por las formulas de vieta se sigue que , por las formulas de vieta se sigue que 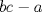 es tambien solucion a esa ecuacion y como es tambien solucion a esa ecuacion y como  se tiene que se tiene que 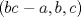 es tambien solucion y como la suma es tambien solucion y como la suma 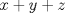 de las soluciones que se van generando van creciendo se sigue que son todas distintas. de las soluciones que se van generando van creciendo se sigue que son todas distintas.
-------------------- "I've never let my school interfere with my education.”
|
|
|
|
 Jul 11 2011, 11:35 AM Jul 11 2011, 11:35 AM
Publicado:
#136
|
|
 Dios Matemático Supremo Grupo: Usuario FMAT Mensajes: 688 Registrado: 8-November 09 Desde: Villarrica Miembro Nº: 61.657 Nacionalidad:  Colegio/Liceo:  Universidad: .png) Sexo:  |
Too mainstream. 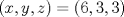 es solucion. Supongamos que tenemos una solucion es solucion. Supongamos que tenemos una solucion 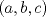 con con 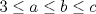 . Tenemos . Tenemos 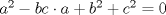 , viendo esa ecuacion como cuadratica en , viendo esa ecuacion como cuadratica en  , por las formulas de vieta se sigue que , por las formulas de vieta se sigue que 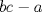 es tambien solucion a esa ecuacion y como es tambien solucion a esa ecuacion y como  se tiene que se tiene que 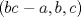 es tambien solucion y como la suma es tambien solucion y como la suma 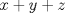 de las soluciones que se van generando van creciendo se sigue que son todas distintas. de las soluciones que se van generando van creciendo se sigue que son todas distintas.Solucion correcta. Proponga -------------------- yo no soy especial
a pesar que ella lo dijo tengo unos krk y un celular hechizo aún vácilo SFDK en el segundo piso y la frase final da igual la improviso |
|
|
|
 Jul 11 2011, 11:52 AM Jul 11 2011, 11:52 AM
Publicado:
#137
|
|
 Dios Matemático Supremo Grupo: Usuario FMAT Mensajes: 532 Registrado: 19-October 08 Desde: Santa Cruz de la Sierra Miembro Nº: 36.531 Nacionalidad:  Sexo:  |
Sean
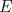 y y 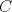 puntos en un semicirculo de diametro puntos en un semicirculo de diametro 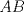 y centro y centro 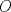 tales que tales que 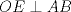 y el punto de interseccion y el punto de interseccion 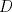 de de 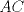 y y 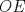 esta dentro del semicirculo. Hallar todos los valores de esta dentro del semicirculo. Hallar todos los valores de 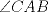 tales que el cuadrilatero tales que el cuadrilatero 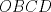 es tangente (osea hay una circunferencia tangente a los 4 lados) es tangente (osea hay una circunferencia tangente a los 4 lados)
Mensaje modificado por xD13G0x el Jul 11 2011, 11:55 AM -------------------- "I've never let my school interfere with my education.”
|
|
|
|
 Jul 26 2011, 06:06 PM Jul 26 2011, 06:06 PM
Publicado:
#138
|
|
|
Doctor en Matemáticas Grupo: Usuario FMAT Mensajes: 192 Registrado: 23-August 10 Miembro Nº: 75.906 Nacionalidad:  Colegio/Liceo:  Sexo:  |
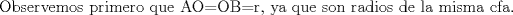 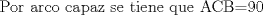 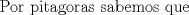 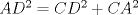 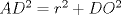 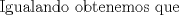 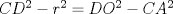 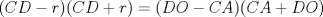 (1) (1)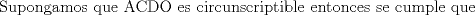 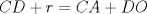 (2), (2), 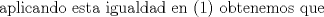 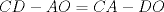 (3) (3)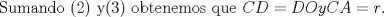 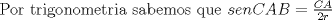 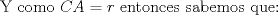 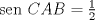 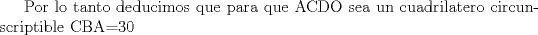 |
|
|
|
 Jul 26 2011, 06:13 PM Jul 26 2011, 06:13 PM
Publicado:
#139
|
|
 Dios Matemático Supremo Grupo: Usuario FMAT Mensajes: 532 Registrado: 19-October 08 Desde: Santa Cruz de la Sierra Miembro Nº: 36.531 Nacionalidad:  Sexo:  |
correcto, lo saque de AoPS de a alguna parte. proponga
-------------------- "I've never let my school interfere with my education.”
|
|
|
|
 Jul 26 2011, 06:25 PM Jul 26 2011, 06:25 PM
Publicado:
#140
|
|
|
Doctor en Matemáticas Grupo: Usuario FMAT Mensajes: 192 Registrado: 23-August 10 Miembro Nº: 75.906 Nacionalidad:  Colegio/Liceo:  Sexo:  |

Mensaje modificado por nagernager el Jul 26 2011, 06:33 PM |
|
|
|
  |
1 usuario(s) está(n) leyendo esta discusión (1 invitado(s) y 0 usuario(s) anónimo(s))
0 miembro(s):
| Versión Lo-Fi | Fecha y Hora actual: 8th July 2025 - 04:00 AM |










