Numeros, numeros y mas numeros

Foro fmat.cl > Sector Preparación Olimpiadas > Sector Olímpico > Teoría de Números > Problemas Propuestos

Numeros, numeros y mas numeros

Opciones

Pasten Ver Perfil del Miembro Ver los mensajes de este miembro	Apr 19 2011, 10:49 PM Publicado: #1
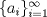Dios Matemático Supremo Grupo: Usuario FMAT Mensajes: 765 Registrado: 6-December 05 Miembro Nº: 458 Nacionalidad: Sexo:	El siguiente problema me parecio interesante: CITA(~Fatal_Collapse~ @ Feb 3 2011, 06:20 PM) Sean $TEX: $p_1,...,p_k$$ primos distintos. Considere todos los enteros positivos que contienen únicamente a esos primos en su factorización canónica (pero no todos necesariamente). Sea $TEX: $\{a_i\}_{i=1}^{\infty}$$ la secuencia infinita creciente de estos enteros. 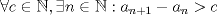Demuestre que $TEX: $\forall c\in \mathbb {N},\exists n\in \mathbb {N}:a_{n+1}-a_n>c$$ . Asi que aqui va una version para los mas valientes: Sean $TEX: $p_1,...,p_k$$ primos distintos. Considere todos los enteros positivos que contienen únicamente a esos primos en su factorización canónica (pero no todos necesariamente). 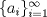Sea $TEX: $\{a_i\}_{i=1}^{\infty}$$ la secuencia infinita creciente de estos enteros. 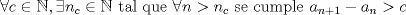Demuestre que $TEX: $\forall c\in \mathbb {N},\exists n_c\in \mathbb {N}$ tal que $\forall n> n_c$ se cumple $a_{n+1}-a_n>c$$ . Saludos -------------------- Pasten, un buen muchacho en quien confiar.

hermite Ver Perfil del Miembro Ver los mensajes de este miembro	Nov 11 2018, 12:10 PM Publicado: #2
Maestro Matemático Grupo: Usuario FMAT Mensajes: 128 Registrado: 27-November 15 Miembro Nº: 142.558	CITA(Pasten @ Apr 19 2011, 10:49 PM) El siguiente problema me parecio interesante: Asi que aqui va una version para los mas valientes: Sean $TEX: $p_1,...,p_k$$ primos distintos. Considere todos los enteros positivos que contienen únicamente a esos primos en su factorización canónica (pero no todos necesariamente). 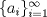Sea $TEX: $\{a_i\}_{i=1}^{\infty}$$ la secuencia infinita creciente de estos enteros. Demuestre que 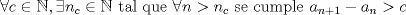$TEX: $\forall c\in \mathbb {N},\exists n_c\in \mathbb {N}$ tal que $\forall n> n_c$ se cumple $a_{n+1}-a_n>c$$ . Saludos $TEX: Partamos por demostrar que para todo $d$, la ecuacion<br />$$a_{n + 1} - a_n = d$$ <br />tiene finitas soluciones (que es equivalente a lo que queremos demostrar).<br />Sea $\mu = (a_{n + 1} ,a_n)$, entonces<br />$$\frac{a_{n + 1}}{\mu} - \frac{a_n}{\mu} = \frac{d}{\mu}$$ <br />(en particular $\mu \leq d$<br />La idea ahora es usar un resultado del tipo ABC para acotar $a_{n + 1}$.<br /><br />$$r = rad(\frac{a_{n + 1}}{\mu} \frac{a_n}{\mu}\frac{d}{\mu})\leq \prod_i^k p_k \frac{d}{\mu}\leq C d$$<br />La penultima desigualdad puesto que $\frac{a_{n+1}}{\mu}$ y $\frac{a_n}{\mu}$ son coprimos y solo tienen los factores primos dados por el problema.<br />Entonces <br />$$\frac{a_{n + 1}}{\mu} \leq e^{K r^{15}}\leq e^{K C^{15} d^{15}}$$<br />$$a_{n + 1} \leq d e^{K C^{15} d^{15}}$$<br />Como $d$ esta fijo y $a_n$ es estrictamente creciente, tenemos una cantidad finita de soluciones a <br />$$a_{n + 1} - a_n = d$$ <br />Para concluir, sea $c\in \mathbb N$, entonces la desigualdad<br />$$a_{n + 1} - a_n \leq c$$ <br />tiene a lo mas finitas soluciones ( es la union de las soluciones de la ecuacion anterior para $d\leq c$), y como $a_n$ es creciente, existe $n_0$ tal que $\forall n\geq n_0,(a_{n+1},a_n)$ no pertenece a ninguna solucion (aqui los parentesis son un par ordenado, no el mcd) y por lo tanto<br />$$\forall n\geq n_0 a_{n +1} - a_n > c$$<br /><br />$

« Posterior · Problemas Propuestos · Anterior »

1 usuario(s) está(n) leyendo esta discusión (1 invitado(s) y 0 usuario(s) anónimo(s))

0 miembro(s):

Modo de Ver: Estándar · Cambiar a: Lineal+ · Cambiar a: Outline

Suscribirse · Enviar por correo · Imprimir · Suscribirse a este foro

Versión Lo-Fi

Fecha y Hora actual: 3rd April 2025 - 09:22 PM