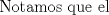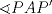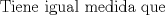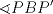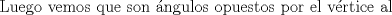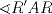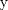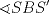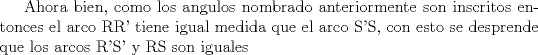|
|
|
|
|
|
|
  |
 Feb 27 2007, 12:23 AM Feb 27 2007, 12:23 AM
Publicado:
#1
|
|
 Dios Matemático Supremo Grupo: Usuario FMAT Mensajes: 558 Registrado: 14-May 05 Desde: Maipú, Stgo, Chile Miembro Nº: 27 Nacionalidad:  Colegio/Liceo:  Universidad:  Sexo:  |
8ª OLIMPIADA NACIONAL DE MATEMÁTICAS Prueba Final Primera Prueba Problema 1: Una marca de zapatos propone: Compre un par de zapatos sin pagar. Se trata de lo siguiente: usted va a la fábrica y paga $20000 por un par de zapatos; recibe los zapatos y diez estampillas, con un costo unitario de $2000. Al vender estas estampillas recuperará su dinero. Quienes compren estas estampillas van a la fábrica, la entregan y por $18000 reciben su par de zapatos y las diez estampillas, continuando así el ciclo. a) ¿Cuánto recibe la fábrica por cada par de zapatos? b) ¿Se puede repetir esta operación cien veces, suponiendo que nadie se repite? Problema 2: Construya el 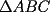 , con , con 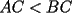 , si se conoce el circuncírculo, y los puntos , si se conoce el circuncírculo, y los puntos 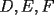 en él, donde vuelven a intersecar, respectivamente, la altura, la mediana y la bisectriz que parten desde el vértice en él, donde vuelven a intersecar, respectivamente, la altura, la mediana y la bisectriz que parten desde el vértice 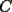 . .Problema 3: Sea 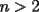 un natural. Dados un natural. Dados 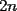 puntos en el plano, tres a tres no colineales, ¿Cuál es el número máximo de trazos que pueden dibujarse entre ellos, sin formar un triángulo? puntos en el plano, tres a tres no colineales, ¿Cuál es el número máximo de trazos que pueden dibujarse entre ellos, sin formar un triángulo?Segunda Prueba Problema 4: Sean 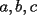 naturales. La ecuación naturales. La ecuación 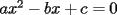 tiene dos raices en tiene dos raices en ![TEX: $[0,1]$](./tex/1172553804.gif) . Pruebe que . Pruebe que 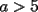 y y 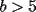 . .Problema 5: Hace un tiempo atrás, en un programa radial, una pastelería anunció una promoción especial en la compra de dos tortas rellenas. Cada torta podía contener hasta cinco rellenos de los que habían en la pastelería. En el programa, una señora decía que habían 1048576 diferentes posibilidades para escoger las dos tortas rellenas. ¿Cuántos rellenos distintos tenía la pastelería?. Problema 6: Dos circunferencias, 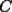 y y 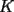 , son secantes en , son secantes en 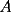 y y 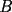 . Sea . Sea 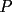 un punto en el arco un punto en el arco 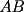 en en 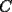 . Las rectas . Las rectas 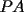 y y 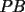 cortan nuevamente a cortan nuevamente a 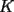 en en 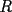 y y 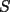 , respectivamente. Sea , respectivamente. Sea 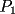 otro punto en el mismo arco que otro punto en el mismo arco que 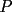 , de modo que las rectas , de modo que las rectas 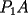 y y 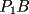 vuelven a intersecar a vuelven a intersecar a 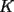 en en 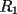 y y 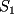 , respectivamente. Pruebe que los arcos , respectivamente. Pruebe que los arcos 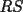 y y 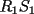 tienen igual medida. tienen igual medida. screen.width*0.6) {this.resized=true; this.width=screen.width*0.4; this.alt='Pincha Aqui para ver esta imagen en su tamaño original';}" onmouseover="if(this.resized) this.style.cursor='hand';" onclick="if(this.resized) {window.open('http://img295.imageshack.us/img295/3747/1996ys7.jpg');}" /> screen.width*0.6) {this.resized=true; this.width=screen.width*0.4; this.alt='Pincha Aqui para ver esta imagen en su tamaño original';}" onmouseover="if(this.resized) this.style.cursor='hand';" onclick="if(this.resized) {window.open('http://img295.imageshack.us/img295/3747/1996ys7.jpg');}" />Problema 7: -------------------- El peor defecto del ignorante es que ignora su propia ignorancia................
|
|
|
|
 May 1 2008, 07:13 PM May 1 2008, 07:13 PM
Publicado:
#2
|
|
 Dios Matemático Supremo Grupo: Usuario FMAT Mensajes: 1.564 Registrado: 12-November 07 Desde: La Union, XIV Region de los Rios Miembro Nº: 12.607 Nacionalidad:  Colegio/Liceo:  Universidad:  Sexo:  |
Problema 6: Dos circunferencias,
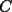 y y 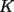 , son secantes en , son secantes en 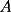 y y 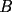 . Sea . Sea 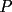 un punto en el arco un punto en el arco 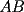 en en 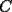 . Las rectas . Las rectas 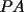 y y 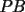 cortan nuevamente a cortan nuevamente a 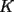 en en 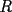 y y 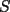 , respectivamente. Sea , respectivamente. Sea 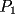 otro punto en el mismo arco que otro punto en el mismo arco que 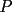 , de modo que las rectas , de modo que las rectas 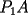 y y 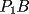 vuelven a intersecar a vuelven a intersecar a 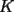 en en 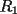 y y 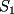 , respectivamente. Pruebe que los arcos , respectivamente. Pruebe que los arcos 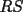 y y 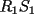 tienen igual medida. tienen igual medida. Saludos PD: sorry por no colocar el dibujo PD2: cual es el P7 ? -------------------- Ricardo Vargas Obando
Ex-alumno Deutsche Schule La Unión (Generación 2010, de los 150 años). Novato de Licenciatura en Matemática/Estadística, en la Pontificia Universidad Católica de Chile.  Grupo de facebook de Novatos Matemática y Estadística PUC 2011 Currículum Olímpico:
|
|
|
|
 May 5 2008, 11:43 AM May 5 2008, 11:43 AM
Publicado:
#3
|
|
 Dios Matemático Supremo Grupo: Administrador Mensajes: 2.706 Registrado: 13-May 05 Desde: Santiago de Chile Miembro Nº: 10 Nacionalidad:  Colegio/Liceo:  Sexo:  |
Ademãs de no incluir una imagen, tu solución no está ordenada. Debes entender que este problema tiene una solución más corta aún.
PD: Intentaremos solucionar rápido la omisión del problema 7... -------------------- |
|
|
|
 May 8 2008, 07:46 PM May 8 2008, 07:46 PM
Publicado:
#4
|
|
|
Dios Matemático Supremo Grupo: Usuario FMAT Mensajes: 878 Registrado: 14-May 07 Desde: Talcahuano Miembro Nº: 5.845 Nacionalidad:  Colegio/Liceo:  Sexo:  |
q tal si (a,b,c)=(1,2,1)? las raices serian (1,1) q estan en [0,1] y a,b,c son naturales.
--------------------  |
|
|
|
 May 8 2008, 08:29 PM May 8 2008, 08:29 PM
Publicado:
#5
|
|
 Coordinador General Gran Maraton PSU Final 2008 Grupo: Moderador Mensajes: 1.607 Registrado: 11-June 07 Desde: Peñalolen, Stgo Miembro Nº: 6.641 Nacionalidad:  Universidad:  Sexo:  |
P6
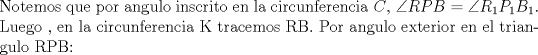 ![TEX: <br />\[<br />\angle RBS = \angle RPB + \angle PRB \Rightarrow \angle RBS - \angle PRB = \angle RPB<br />\]<br /><br />](./tex/d9bd3f8e5805edbd701c8091987cb68c.png) 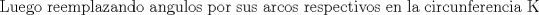 ![TEX: \[<br />\frac{\stackrel{\displaystyle\frown}{RS} - \stackrel{\displaystyle\frown}{AB}}<br />{2} = \angle RPB<br />\]<br />](./tex/13ff5374929e0d862b1d54e24c97deae.png) 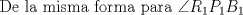 ![TEX: \[<br />\frac{\stackrel{\displaystyle\frown}{R_1S_1} - \stackrel{\displaystyle\frown}{AB}}<br />{2} = \angle R_1P_1B_1<br />\]<br />](./tex/c59eec9a12de695b50febe64ca1f10bc.png) 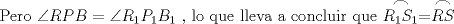
Mensaje modificado por CyedqD el May 8 2008, 08:29 PM --------------------  |
|
|
|
 Jun 12 2008, 09:48 PM Jun 12 2008, 09:48 PM
Publicado:
#6
|
|
|
Doctor en Matemáticas Grupo: Usuario FMAT Mensajes: 153 Registrado: 27-March 08 Desde: calle santa maria 221 Miembro Nº: 18.096 Nacionalidad:  Colegio/Liceo:  Sexo:  |
bueno los intentare hacer
chaoxxxxxxxxxxx -------------------- manuxxx
|
|
|
|
 Mar 15 2009, 07:11 PM Mar 15 2009, 07:11 PM
Publicado:
#7
|
|
 Dios Matemático Supremo Grupo: Usuario FMAT Mensajes: 1.564 Registrado: 12-November 07 Desde: La Union, XIV Region de los Rios Miembro Nº: 12.607 Nacionalidad:  Colegio/Liceo:  Universidad:  Sexo:  |
Problema 2: Construya el 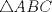 , con , con 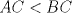 , si se conoce el circuncírculo, y los puntos , si se conoce el circuncírculo, y los puntos 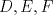 en él, donde vuelven a intersecar, respectivamente, la altura, la mediana y la bisectriz que parten desde el vértice en él, donde vuelven a intersecar, respectivamente, la altura, la mediana y la bisectriz que parten desde el vértice 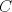 . . Olimpiada_nacional_1996.png ( 88.79k )
Número de descargas: 6
Olimpiada_nacional_1996.png ( 88.79k )
Número de descargas: 6Llamemos 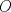 al circumcentro del al circumcentro del 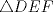 . Como . Como 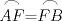 (por ser (por ser 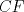 bisectriz del bisectriz del 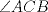 ); se sigue que ); se sigue que 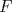 pertenece a la mediatriz de pertenece a la mediatriz de 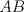 . Por otra parte, como . Por otra parte, como 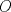 tambien pertenece a la mediatriz de tambien pertenece a la mediatriz de 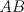 ; obtenemos que ; obtenemos que 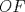 es perpendicular a es perpendicular a 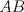 . Ademas, sabemos que . Ademas, sabemos que 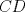 tambien es perpendicular a tambien es perpendicular a 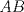 . Esto implica que . Esto implica que  . Como conocemos los puntos . Como conocemos los puntos 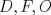 ; podemos determinar la ubicacion de ; podemos determinar la ubicacion de 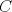 trazando la paralela a trazando la paralela a 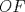 que pasa por que pasa por 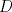 . El punto donde esta paralela interseca a la circunferencia (distinto de . El punto donde esta paralela interseca a la circunferencia (distinto de 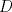 ) sera el vertice ) sera el vertice 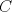 Llamemos 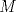 al punto medio de al punto medio de 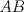 . Notemos que . Notemos que 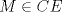 ; y ; y 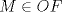 (por ser (por ser 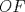 la mediatriz de la mediatriz de 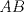 ); luego ); luego 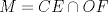 . Como . Como 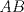 es perpendicular a es perpendicular a 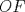 , para determinar , para determinar 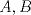 debemos trazar una recta perpendicular a debemos trazar una recta perpendicular a 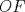 que pase por que pase por 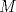 . Los puntos donde esta recta interseca a la circunferencia seran . Los puntos donde esta recta interseca a la circunferencia seran 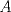 y y 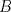 . Ahora, el punto que este a menor distancia de . Ahora, el punto que este a menor distancia de 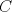 sera sera 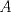 , y el otro sera , y el otro sera 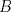 , finalizando la construccion , finalizando la construccion 
-------------------- Ricardo Vargas Obando
Ex-alumno Deutsche Schule La Unión (Generación 2010, de los 150 años). Novato de Licenciatura en Matemática/Estadística, en la Pontificia Universidad Católica de Chile.  Grupo de facebook de Novatos Matemática y Estadística PUC 2011 Currículum Olímpico:
|
|
|
|
 Aug 19 2012, 01:11 PM Aug 19 2012, 01:11 PM
Publicado:
#8
|
|
 Maestro Matemático Grupo: Usuario FMAT Mensajes: 100 Registrado: 17-April 11 Miembro Nº: 87.227 Nacionalidad:  Colegio/Liceo:  Universidad:  Sexo:  |
Una solución un poco mas corta al P6
--------------------    |
|
|
|
 Aug 19 2012, 01:21 PM Aug 19 2012, 01:21 PM
Publicado:
#9
|
|
|
Dios Matemático Supremo Grupo: Usuario FMAT Mensajes: 9.897 Registrado: 6-April 08 Miembro Nº: 19.238 Nacionalidad:  Colegio/Liceo:  Sexo:  |
Buena solución cristóbal! de hecho así se demuestra de manera corta que en ese mismo diagrama, la longitud del segmento R'S' no depende de la posición del punto P'. (problema bien conocido de ese apunte mexicano que una vez linkeó el kenshin)
-------------------- |
|
|
|
 Aug 19 2012, 01:33 PM Aug 19 2012, 01:33 PM
Publicado:
#10
|
|
 Maestro Matemático Grupo: Usuario FMAT Mensajes: 100 Registrado: 17-April 11 Miembro Nº: 87.227 Nacionalidad:  Colegio/Liceo:  Universidad:  Sexo:  |
Buena solución cristóbal! de hecho así se demuestra de manera corta que en ese mismo diagrama, la longitud del segmento R'S' no depende de la posición del punto P'. (problema bien conocido de ese apunte mexicano que una vez linkeó el kenshin) Gracias!, tendré que ver ese apunte, ahora que se aproxima la Nacional jajaja, no me había dado cuenta lo que pronunciaste --------------------    |
|
|
|
  |
1 usuario(s) está(n) leyendo esta discusión (1 invitado(s) y 0 usuario(s) anónimo(s))
0 miembro(s):
| Versión Lo-Fi | Fecha y Hora actual: 2nd April 2025 - 02:28 AM |