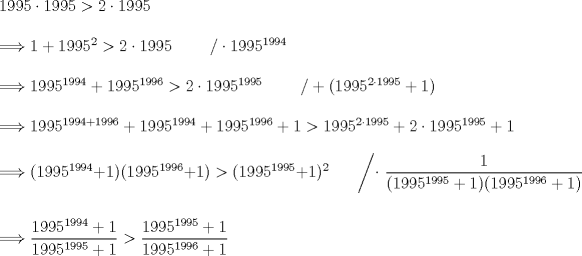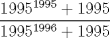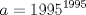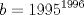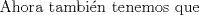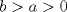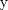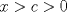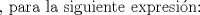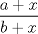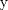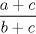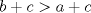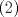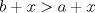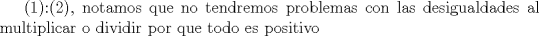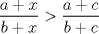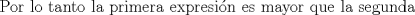Prueba Final (1995) - Foro fmat.cl

Portal Matemático

¿Qué es FMAT?

Foro fmat.cl > Sector Preparación Olimpiadas > Competencias y Olimpiadas > Olimpiadas > Olimpiada Nacional

2 Páginas:

1 2 >

Reply to this topic

Start new topic

Prueba Final (1995), Sin solución: 1,2,3,4,5,6,7

Gp20 Ver Perfil del Miembro Ver los mensajes de este miembro	Feb 27 2007, 12:01 AM Publicado: #1
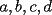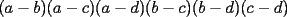Dios Matemático Supremo Grupo: Usuario FMAT Mensajes: 558 Registrado: 14-May 05 Desde: Maipú, Stgo, Chile Miembro Nº: 27 Nacionalidad: Colegio/Liceo: Universidad: Sexo:	7ª OLIMPIADA NACIONAL DE MATEMÁTICAS Prueba Final Primera Prueba Problema 1: Sean $TEX: $a, b, c, d$$ enteros. Pruebe que 12 divide a $TEX: $(a-b)(a-c)(a-d)(b-c)(b-d)(c-d)$$ . Problema 2: En un círculo de radio 1 se dibujan seis arcos de radio 1, que cortan al círculo como en la figura. Determine el área negra. 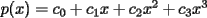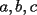screen.width0.6) {this.resized=true; this.width=screen.width0.4; this.alt='Pincha Aqui para ver esta imagen en su tamaÃ±o original';}" onmouseover="if(this.resized) this.style.cursor='hand';" onclick="if(this.resized) {window.open('http://img263.imageshack.us/img263/4011/19951zp8.jpg');}" /> Problema 3: Si $TEX: $p(x)=c_0+c_1x+c_2x^2+c_3x^3$$ es un polinomio con coeficientes enteros con $TEX: $a, b, c$$ enteros y distintos entre sí, pruebe que no puede ocurrir simultáneamente que: i) 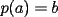$TEX: $p(a)=b$$ ii) 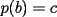$TEX: $p(b)=c$$ iii) 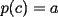$TEX: $p©=a$$ Segunda Prueba Problema 4: ¿Es posible escribir los números 111, 112, 121, 122, 211, 212, 221 y 222 en los vértices de un cubo, de modo que los números escritos en vértices adyacentes coincidan a lo más en un dígito? Problema 5: Un domador quiere alinear cinco leones y cuatro tigres. Sabiendo que un tigre no puede ir detrás de otro, ¿De cuántas maneras se pueden distribuir las fieras?. El domador no puede distinguir dos animales de la misma especie. 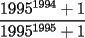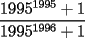Problema 6: ¿Cuál de los siguientes racionales es mayor: $TEX: $\dfrac{1995^{1994}+1}{1995^{1995}+1}$$ o $TEX: $\dfrac{1995^{1995}+1}{1995^{1996}+1}$$ ? Problema 7: En un semicírculo de radio 4 se inscriben tres círculos, como indica la figura. 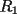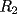Las circunferencias mayores tienen radios $TEX: $R_1$$ y $TEX: $R_2$$ , y la circunferencia mayor tiene radio $TEX: $r$$ . screen.width0.6) {this.resized=true; this.width=screen.width0.4; this.alt='Pincha Aqui para ver esta imagen en su tamaÃ±o original';}" onmouseover="if(this.resized) this.style.cursor='hand';" onclick="if(this.resized) {window.open('http://img263.imageshack.us/img263/9352/19952gi0.jpg');}" /> a) Pruebe que 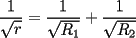$TEX: $\dfrac{1}{\sqrt{r}}=\dfrac{1}{\sqrt{R_1}}+\dfrac{1}{\sqrt{R_2}}$$ b) Pruebe que 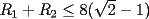$TEX: $R_1+R_2\le 8(\sqrt{2}-1)$$ c) Pruebe que 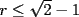$TEX: $r\le \sqrt{2}-1$$ -------------------- El peor defecto del ignorante es que ignora su propia ignorancia................ Educación2020 - Registra tu apoyo individual!!!!

wenopagozar Ver Perfil del Miembro Ver los mensajes de este miembro	Jan 4 2008, 11:15 PM Publicado: #2
Dios Matemático Grupo: Usuario FMAT Mensajes: 260 Registrado: 6-June 07 Miembro Nº: 6.476	CITA(Gp20 @ Feb 27 2007, 02:01 AM) Problema 6: ¿Cuál de los siguientes racionales es mayor: $TEX: $\dfrac{1995^{1994}+1}{1995^{1995}+1}$$ o $TEX: $\dfrac{1995^{1995}+1}{1995^{1996}+1}$$ ? $TEX: \noindent $1995 \cdot 1995 > 2 \cdot 1995$\\<br />\\<br />$\Longrightarrow 1 + 1995^2 > 2 \cdot 1995 \ \ \ \ \ \ \ / \cdot 1995^{1994}$\\<br />\\<br />$\Longrightarrow 1995^{1994} + 1995^{1996} > 2 \cdot 1995^{1995} \ \ \ \ \ \ \ / + (1995^{2 \cdot 1995} + 1)$\\<br />\\<br />$\Longrightarrow 1995^{1994+1996} + 1995^{1994} + 1995^{1996} + 1 > 1995^{2 \cdot 1995} + 2 \cdot 1995^{1995} + 1$\\<br />\\<br />$\Longrightarrow (1995^{1994}+1)(1995^{1996}+1)>(1995^{1995}+1)^2 \ \ \ \ \ \ \ \left/ \cdot \ \dfrac1{(1995^{1995}+1)(1995^{1996}+1)} \right.$\\<br />\\<br />\\<br />$\Longrightarrow \dfrac{1995^{1994}+1}{1995^{1995}+1}>\dfrac{1995^{1995}+1}{1995^{1996}+1}$<br />$

S. E. Puelma Moy... S. E. Puelma Moya Ver Perfil del Miembro Ver los mensajes de este miembro	Jan 7 2008, 06:15 AM Publicado: #3
Dios Matemático Supremo Grupo: Administrador Mensajes: 2.706 Registrado: 13-May 05 Desde: Santiago de Chile Miembro Nº: 10 Nacionalidad: Colegio/Liceo: Sexo:	Solución correcta... queda un ejercicio menos en esta prueba -------------------- Sebastián Elías Puelma Moya Administrador FMAT

Naxoo Ver Perfil del Miembro Ver los mensajes de este miembro	Jan 12 2008, 11:16 PM Publicado: #4
Staff FMAT Grupo: Moderador Mensajes: 2.604 Registrado: 2-March 07 Desde: Somewhere over the rainbow Miembro Nº: 4.244 Nacionalidad: Colegio/Liceo: Universidad: Sexo:	CITA Problema 2: En un círculo de radio 1 se dibujan seis arcos de radio 1, que cortan al círculo como en la figura. Determine el área negra. screen.width0.6) {this.resized=true; this.width=screen.width0.4; this.alt='Pincha Aqui para ver esta imagen en su tamaÃ±o original';}" onmouseover="if(this.resized) this.style.cursor='hand';" onclick="if(this.resized) {window.open('http://img263.imageshack.us/img263/4011/19951zp8.jpg');}" /> yo lo vi de esta forma: que los arcos son pertenecientes a otras circunferencias de esta forma: (la gracia es haber podido dibujar las 6 circunferencias, pero pude hacerlo ) k.png ( 19.78k ) Número de descargas: 7 ahora si trazamos todas las rectas que unan los puntos de interseccion de los arcos con la circunferencia, estariamos formando un hexagono regular, que se compone de 6 triangulos equilateros de lado igual al radio, entonces: $TEX: % MathType!MTEF!2!1!+-<br />% feaafiart1ev1aaatCvAUfeBSjuyZL2yd9gzLbvyNv2CaerbuLwBLn<br />% hiov2DGi1BTfMBaeXatLxBI9gBaerbd9wDYLwzYbItLDharqqtubsr<br />% 4rNCHbGeaGqiVu0Je9sqqrpepC0xbbL8F4rqqrFfpeea0xe9Lq-Jc9<br />% vqaqpepm0xbba9pwe9Q8fs0-yqaqpepae9pg0FirpepeKkFr0xfr-x<br />% fr-xb9adbaqaaeGaciGaaiaabeqaamaabaabaaGceaqabeaacqWIZw<br />% IvcaWGbbGaamOqaiaad+eacqGHNis2cqWIZwIvcaWGbbGaamOqaiqa<br />% d+eagaqbaiaabccacaqGZbGaae4Baiaab6gacaqGGaGaaeyzaiaabg<br />% hacaqG1bGaaeyAaiaabYgacaqGHbGaaeiDaiaabwgacaqGYbGaae4B<br />% aiaabohacaqGGaGaae4yaiaab+gacaqGUbGaae4zaiaabkhacaqG1b<br />% Gaaeyzaiaab6gacaqG0bGaaeyzaiaabohacaqGGaGaaeizaiaabwga<br />% caqGGaGaaeiBaiaabggacaqGKbGaae4BaiaabccacaqGPbGaae4zai<br />% aabwhacaqGHbGaaeiBaiaabccacaqGHbGaaeymaiaabYcacaqGGaGa<br />% ae4yaiaabggacaqGSbGaae4yaiaabwhacaqGSbGaaeyzaiaab2gaca<br />% qGVbGaae4CaiaabccacaqGLbGaaeiBaiaabccacaqGHbGaaeOCaiaa<br />% bwgacaqGHbaabaGaaeizaiaabwgacaqGGaGaae4yaiaabwhacaqGHb<br />% GaaeiBaiaabghacaqG1bGaaeyAaiaabwgacaqGYbGaaeyyaiaabcca<br />% caqGKbGaaeyzaiaabccacaqGSbGaae4BaiaabohacaqGGaGaaeizai<br />% aab+gacaqGZbGaaeiiaiaabohacaqGLbGaae4yaiaabshacaqGVbGa<br />% aeOCaiaabwgacaqGZbGaaeiiaiaabogacaqGPbGaaeOCaiaabogaca<br />% qG1bGaaeiBaiaabggacaqGYbGaaeyzaiaabohacaqG6aaabaaabaWa<br />% aSaaaeaacqaHapaCcaWGYbWaaWbaaSqabeaacaaIYaaaaaGcbaGaam<br />% 4uaiaac6cacaWGdbaaaiabg2da9maalaaabaGaaG4maiaaiAdacaaI<br />% WaaabaGaaGOnaiaaicdaaaGaeyi1HS9aaucfaeaacaWGtbGaaiOlai<br />% aadoeacqGH9aqpdaWcaaqaaiabec8aWjaadkhadaahaaWcbeqaaiaa<br />% ikdaaaaakeaacaaI2aaaaaaaaeaaaeaacaqGZbGaaeyAaiaabccaca<br />% qGHbGaaeiBaiaabccacaqGtbGaaeOlaiaaboeacaqGGaGaae4Caiaa<br />% bwgacaqGGaGaaeiBaiaabwgacaqGGaGaaeOCaiaabwgacaqGZbGaae<br />% iDaiaabggacaqGGaGaaeyzaiaabYgacaqGGaGaaeyyaiaabkhacaqG<br />% LbGaaeyyaiaabccacaqGKbGaaeyzaiaabYgacaqGGaGaeS4SLyLaam<br />% yqaiaadkeacaWGpbGaaeiiaiaab+gacaqGGaGaaeizaiaabwgacaqG<br />% SbGaaeiiaiabloBjwjaadgeacaWGcbGabm4tayaafaGaaeiiaiaab+<br />% gacaqGIbGaaeiDaiaabwgacaqGUbGaaeizaiaabkhacaqGPbGaaeyy<br />% aiaab2gacaqGVbGaae4CaiaabccacaqGSbGaaeyyaiaabccacaqGTb<br />% GaaeyAaiaabshacaqGHbGaaeizaiaabccacaqGKbGaaeyzaiaabYga<br />% caqGGaGaaeyyaiaabkhacaqGLbGaaeyyaiaabccacaqGJbGaae4Bai<br />% aab2gacaqGWbGaaeOCaiaabwgacaqGUbGaaeizaiaabMgacaqGHbaa<br />% baGaaeiCaiaab+gacaqGYbGaaeiiaiaabYgacaqGVbGaae4Caiaabc<br />% cacaqGHbGaaeOCaiaabogacaqGVbGaae4CaiaabccacaqGKbGaaeyz<br />% aiaabccacaqGSbGaaeyyaiaabccacaqGMbGaaeyAaiaabEgacaqG1b<br />% GaaeOCaiaabggacaqGGaGaaeyAaiaab6gacaqGPbGaae4yaiaabMga<br />% caqGHbGaaeiBaiaabccacaqGOaGaaeiBaiaabggacaqGGaGaaeyBai<br />% aabMgacaqG0bGaaeyyaiaabsgacaqGGaGaaeizaiaabwgacaqGGaGa<br />% ae4yaiaabggacaqGKbGaaeyyaiaabccacaqG1bGaaeOBaiaabggaca<br />% qGGaGaaeizaiaabwgacaqGGaGaaeiBaiaabggacaqGZbGaaeiiaiaa<br />% bchacaqGHbGaaeOCaiaabshacaqGLbGaae4CaiaabccacaqGIbGaae<br />% iBaiaabggacaqGUbGaae4yaiaabggacaqGZbGaaeykaaqaaaqaaiaa<br />% b2gacaqGPbGaaeiDaiaabggacaqGKbGaaeiiaiaabchacaqGHbGaae<br />% OCaiaabshacaqGLbGaaeiiaiaabkgacaqGSbGaaeyyaiaab6gacaqG<br />% JbGaaeyyaiaab2dadaWcaaqaaiabec8aWjaadkhadaahaaWcbeqaai<br />% aaikdaaaaakeaacaaI2aaaaiabgkHiTmaalaaabaWaaOaaaeaacaaI<br />% ZaaaleqaaaGcbaGaaGinaaaaaeaaaeaacaqGWbGaaeyyaiaabkhaca<br />% qG0bGaaeyzaiaabccacaqGIbGaaeiBaiaabggacaqGUbGaae4yaiaa<br />% bggacaqG9aGaaeOmamaabmaabaWaaSaaaeaacaaIYaGaeqiWdaNaam<br />% OCamaaCaaaleqabaGaaGOmaaaakiabgkHiTiaaiodadaGcaaqaaiaa<br />% iodaaSqabaaakeaacaqGXaGaaeOmaaaaaiaawIcacaGLPaaaaeaaae<br />% aacaWGqbGaaiOlaiaadkeacqGH9aqpdaWcaaqaaiaaikdacqaHapaC<br />% caWGYbWaaWbaaSqabeaacaaIYaaaaOGaeyOeI0IaaG4mamaakaaaba<br />% GaaG4maaWcbeaaaOqaaiaabAdaaaaabaaabaGaaeyyaiaabIgacaqG<br />% VbGaaeOCaiaabggacaqGGaGaaeiCaiaabggacaqGYbGaaeyyaiaabc<br />% cacaqGJbGaaeyyaiaabYgacaqG1bGaae4yaiaabwhacaqGSbGaaeyy<br />% aiaabkhacaqGGaGaaeiDaiaab+gacaqGKbGaaeyyaiaabohacaqGGa<br />% GaaeiBaiaabggacaqGZbGaaeiiaiaabchacaqGHbGaaeOCaiaabsha<br />% caqGLbGaae4CaiaabccacaqGIbGaaeiBaiaabggacaqGUbGaae4yai<br />% aabwgacaqGZbGaaeiiaiaab2gacaqG1bGaaeiBaiaabshacaqGPbGa<br />% aeiCaiaabYgacaqGPbGaae4yaiaabggacaqGTbGaae4Baiaabohaca<br />% qGGaGaaeiCaiaab+gacaqGYbGaaeiiaiaabAdaaeaaaeaacaqGubGa<br />% aeOlaiaabcfacaqGUaGaaeOqaiaab2dacaaIYaGaeqiWdaNaamOCam<br />% aaCaaaleqabaGaaGOmaaaakiabgkHiTiaaiodadaGcaaqaaiaaioda<br />% aSqabaaakeaaaeaacaqGLbGaaeiBaiaabccacaqGHbGaaeOCaiaabw<br />% gacaqGHbGaaeiiaiaabchacaqGLbGaaeizaiaabMgacaqGKbGaaeyy<br />% aiaabccacaqGZbGaaeyzaiaabccacaqGJbGaaeyyaiaabYgacaqGJb<br />% GaaeyDaiaabYgacaqGHbGaaeiiaiaabsgacaqGLbGaaeiiaiaabYga<br />% caqGHbGaaeiiaiaabohacaqGPbGaae4zaiaabwhacaqGPbGaaeyzai<br />% aab6gacaqG0bGaaeyzaiaabccacaqGMbGaae4BaiaabkhacaqGTbGa<br />% aeyyaiaabQdaaeaaaeaacaqGbbGaaeiEaiaab2dacaqGbbGaeSyMIu<br />% MaaeylaiaabsfacaqGUaGaaeiuaiaab6cacaqGcbaabaaabaGaaeyq<br />% aiaabIhacaqG9aGaeqiWdaNaamOCamaaCaaaleqabaGaaGOmaaaaki<br />% abgkHiTmaabmaabaGaaGOmaiabec8aWjaadkhadaahaaWcbeqaaiaa<br />% ikdaaaGccqGHsislcaaIZaWaaOaaaeaacaaIZaaaleqaaaGccaGLOa<br />% GaayzkaaaabaaabaWaauIhaeaacaWGbbGaamiEaiabg2da9iaaioda<br />% daGcaaqaaiaaiodaaSqabaGccqGHsislcqaHapaCcaWGYbWaaWbaaS<br />% qabeaacaaIYaaaaaaaaaaa!13AA!<br />\[<br />\begin{gathered}<br /> \vartriangle ABO \wedge \vartriangle ABO'{\text{ son equilateros congruentes de lado igual a1}}{\text{, calculemos el area}} \hfill \\<br /> {\text{de cualquiera de los dos sectores circulares:}} \hfill \\<br /> \hfill \\<br /> \frac{{\pi r^2 }}<br />{{S.C}} = \frac{{360}}<br />{{60}} \Leftrightarrow \left. {\underline {\, <br /> {S.C = \frac{{\pi r^2 }}<br />{6}} \,}}\! \right\| \hfill \\<br /> \hfill \\<br /> {\text{si al S}}{\text{.C se le resta el area del }}\vartriangle ABO{\text{ o del }}\vartriangle ABO'{\text{ obtendriamos la mitad del area comprendia}} \hfill \\<br /> {\text{por los arcos de la figura inicial (la mitad de cada una de las partes blancas)}} \hfill \\<br /> \hfill \\<br /> {\text{mitad parte blanca = }}\frac{{\pi r^2 }}<br />{6} - \frac{{\sqrt 3 }}<br />{4} \hfill \\<br /> \hfill \\<br /> {\text{parte blanca = 2}}\left( {\frac{{2\pi r^2 - 3\sqrt 3 }}<br />{{{\text{12}}}}} \right) \hfill \\<br /> \hfill \\<br /> P.B = \frac{{2\pi r^2 - 3\sqrt 3 }}<br />{{\text{6}}} \hfill \\<br /> \hfill \\<br /> {\text{ahora para calucular todas las partes blances multiplicamos por 6}} \hfill \\<br /> \hfill \\<br /> {\text{T}}{\text{.P}}{\text{.B = }}2\pi r^2 - 3\sqrt 3 \hfill \\<br /> \hfill \\<br /> {\text{el area pedida se calcula de la siguiente forma:}} \hfill \\<br /> \hfill \\<br /> {\text{Ax = A}} \odot {\text{ - T}}{\text{.P}}{\text{.B}} \hfill \\<br /> \hfill \\<br /> {\text{Ax = }}\pi r^2 - \left( {2\pi r^2 - 3\sqrt 3 } \right) \hfill \\<br /> \hfill \\<br /> \boxed{Ax = 3\sqrt 3 - \pi r^2 } \hfill \\ <br />\end{gathered} <br />\]<br />$ finalmente pido disculpas por decir "partes blancas" ya que se me olvido el nombre de aquel sector Mensaje modificado por naxoobkn el Jan 13 2008, 10:39 AM -------------------- INRIA - Francia, Sophia Antipolis Biocore Team Ingeniero Civil en Biotecnología Ingeniería Civil Químico “(…) los elementos que él (¿o Él?) [Dios] mismo nos ha dado (raciocinio, sensibilidad, intuición) no son en absoluto suficientes como para garantizarnos ni su existencia ni su no existencia. Gracias a una corazonada puedo creer en Dios y acertar o no creer en Dios y también acertar" Mario Benedetti $TEX: \[\iiint\limits_\Omega {\left( {\nabla \cdot \vec F} \right)dV} = \iint\limits_{\partial \Omega } {\left( {\vec F \cdot \hat n} \right)}dS\]<br />$

S. E. Puelma Moy... S. E. Puelma Moya Ver Perfil del Miembro Ver los mensajes de este miembro	Jan 14 2008, 07:54 AM Publicado: #5
Dios Matemático Supremo Grupo: Administrador Mensajes: 2.706 Registrado: 13-May 05 Desde: Santiago de Chile Miembro Nº: 10 Nacionalidad: Colegio/Liceo: Sexo:	Creo que seguí todo tu argumento, y está correcto , el nombre de las partes blancas es "segmento circular" (la región limitada por una cuerda y un arco de circunferencia) PD: En todas las partes que usaste el radio de la circunferencia, olvidaste que éste mide 1 -------------------- Sebastián Elías Puelma Moya Administrador FMAT

p.j.t Ver Perfil del Miembro Ver los mensajes de este miembro	Jan 31 2008, 10:19 PM Publicado: #6
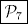Dios Matemático Supremo Grupo: Usuario FMAT Mensajes: 766 Registrado: 6-May 07 Desde: San Pedro de la Paz, Concepción Miembro Nº: 5.639 Nacionalidad: Colegio/Liceo: Sexo:	supongo que $TEX: $r$$ es el radio de la circ. menor $TEX: \boxed{\mathcal{P}_{7}}$ SEMI.png ( 19.05k ) Número de descargas: 4 $TEX: Usaremos la notaci\'on de la figura, siendo $XA=R_1$ y $YB=R_2$ \\<br />$(a)$ Sean CY y ZD perpendiculares a XA y ZE perpendicular a YB. Notemos que $XY=R_1+R_2$ y $XC=R_1-R_2$. Sea $\alpha=CY$. Como el $\triangle XCY$ es rectangulo por teorema de pitagoras:\\ $\begin{aligned} (R_1-R_2)^2+\alpha^2&=(R_1+R_2)^2 \\ R_1^2-2R_1R_2+R_2^2+\alpha^2&=R_1^2+2R_1R_2+R_2^2 \\ \alpha^2-2R_1R_2&=2R_1R_2 \\ \alpha^2&=4R_1R_2 \\ \alpha&=2\sqrt{R_1R_2} \end{aligned}$ \\ Analogamente trabajando con $(R_1,r)$ y $(R_2,r)$ obtenemos que : $$(R_1-r)^2+DZ^2=(R_1+r)^2 \implies DZ=2\sqrt{R_1r}$$ $$(R_2-r)^2 +EZ^2=(R_2+r)^2 \implies EZ=2\sqrt{R_2r}$$ No es dificil notar que tenemos un rectangulo CDEY (debido a los angulos rectos), luego:\\ $\begin{aligned} CY&=DE \\ CY&=DZ+ZE \\ 2\sqrt{R_1R_2}&=2\sqrt{R_1r}+2\sqrt{R_2r} \Big/ \div (2\sqrt{R_1R_2r}) \\ \dfrac1{\sqrt{r}}&=\dfrac1{\sqrt{R_1}}+ \dfrac1{\sqrt{R_2}} \end{aligned}$\\ Como se queria (no hubo problemas en dividir pues dividimos por un positivo).$ Otro dia sigo con las otras, ahora tengo sueño Saludos -------------------- asdf

JoNy_SaTiE Ver Perfil del Miembro Ver los mensajes de este miembro	Feb 6 2008, 09:18 AM Publicado: #7
Dios Matemático Supremo Grupo: Colaborador Gold Mensajes: 1.118 Registrado: 11-September 05 Desde: Valdivia/Ancud Miembro Nº: 302 Nacionalidad: Colegio/Liceo: Universidad: Sexo:	$TEX: P1<br /><br />Si $x$ es un entero, $x \equiv 0,1,2 \pmod 3$.<br /><br />Entonces con cuatro enteros a,b,c,d. Siempre exitirán al menos dos de ellos con la misma congruencia módulo 3. Luego la diferencia entre ellos resultará en un múltiplo de 3. Digamos $x \equiv z \pmod 3$ e $y \equiv z \pmod 3$. $x-y \equiv 0 \pmod 3$. Con esto, $3\|(a-b)(a-c)(a-d)(b-c)(b-d)(c-d)$.<br />\vspace{5mm}<br />Si $x$ es un entero, $x \equiv 0,1 \pmod 2$.<br /><br />Ahora se puede separar en casos. Considerando cuatro enteros a,b,c y d:<br /><br />\begin{itemize}<br />\item[Caso 1] Todos tienen la misma congruencia módulo 2. Aquí es trivial, $12\|(a-b)(a-c)(a-d)(b-c)(b-d)(c-d) \Rightarrow 4\|(a-b)(a-c)(a-d)(b-c)(b-d)(c-d) $.<br />\item[Caso 2] Tres de ellos tienen la misma congruencia módulo. Sin pérdida de generalidad (por la simetría existente), supongamos que $a \equiv 0 \pmod 2$ y que $b,c,d \equiv 1 \pmod 2$. Luego $6\|(a-b)(a-c)(a-d)(b-c)(b-d)(c-d) \Rightarrow 4\|(a-b)(a-c)(a-d)(b-c)(b-d)(c-d) $.<br /><br />\item[Caso 3] Hay dos pares de números congruentes. Sin pérdida de generalidad, digamos que $a,b \equiv 0 \pmod 2$ y que $c,d \equiv 1 \pmod 2$. Luego $4\|(a-b)(a-c)(a-d)(b-c)(b-d)(c-d)$.<br />\end{itemize}<br /><br />Como 4 y 3 dividen la expresión, se prueba que $12\|(a-b)(a-c)(a-d)(b-c)(b-d)(c-d) $.<br />$ -------------------- Comienza a crear documentos con LaTeX. Ya usas LaTeX y quieres aprender un poco más ... pincha aquí Si eres de la UaCH ... únete a la causa !!! J. Jonathan H. Oberreuter A. Universidad Austral de Chile - RWTH Aachen alumni Est. Magister en Acústica y Vibraciones Ingeniero Civil Acústico (E) Bachiller y Licenciado en Cs. de la Ingeniería

Pedantic Anarchy... Pedantic Anarchy Ver Perfil del Miembro Ver los mensajes de este miembro	Jun 7 2010, 05:11 PM Publicado: #8
Dios Matemático Supremo Grupo: Usuario FMAT Mensajes: 688 Registrado: 8-November 09 Desde: Villarrica Miembro Nº: 61.657 Nacionalidad: Colegio/Liceo: Universidad: Sexo:	$TEX: Notemos que $a-b\|P(a)-P(b)=c_1(a-b)+c_2(a^2-b^2)+c_3(a^3-b^3)$, ya que $a-b\|(a^n-b^n)$, entonces $a-b\|b-c$. Homologamente $a-c\|b-a$,$b-c\|c-a$. Por otra parte tenemos que si $a\|b$ entonces $\|a\|\le \|b\|$, por lo tanto $\|a-b\|\le \|b-c\|\le \|c-a\|=\|a-c\|\le \|b-a\|$, pero $\|b-a\|=\|a-b\|$, entonces $\|a-b\|=\|b-c\|=\|c-a\|$. W.L.O.G $a\ge b\ge c$, por lo tanto $a-b=b-c=a-c$, donde claramente $a=b=c$, lo que contradice el enunciado, en consecuencia no existen $a,b,c$ enteros y distintos que cumplan con tales condiciones$ -------------------- yo no soy especial a pesar que ella lo dijo tengo unos krk y un celular hechizo aún vácilo SFDK en el segundo piso y la frase final da igual la improviso

Newtype Ver Perfil del Miembro Ver los mensajes de este miembro	Oct 9 2010, 10:55 PM Publicado: #9
Dios Matemático Supremo Grupo: Team Ensayos FMAT Mensajes: 1.559 Registrado: 18-November 07 Miembro Nº: 12.754 Nacionalidad: Sexo:	CITA(Gp20 @ Feb 27 2007, 01:01 AM) Problema 4: ¿Es posible escribir los números 111, 112, 121, 122, 211, 212, 221 y 222 en los vértices de un cubo, de modo que los números escritos en vértices adyacentes coincidan a lo más en un dígito? Sí es posible, aquí va una conformación: Si el cuadrado chico representa la cara superior, y el grande la inferior, del cubo... prob_4.jpg ( 9.49k ) Número de descargas: 3 Primero, coloqué el 111 en el vértice donde aparece. Luego, me fijé de colocar en los 3 vértices adyacentes al donde se encontraba este número, números que coincidieran en máximo 1 dígito con el 111. Así, seguí adelante, fijándome en ese mismo detalle las veces restantes.Cada vez va siendo más obvio dónde colocar los numeros, ya que se descartan otros vertices, según los dígitos de sus números adyacentes. Con esto no se demuestra que esta sea la única configuración posible, pero por lo menos se muestra una que es válida. Saludos... -------------------- Empezando con Desigualdades? Encuentra aquí problemas resueltos

Cristóbaal Ver Perfil del Miembro Ver los mensajes de este miembro	Aug 19 2012, 01:08 AM Publicado: #10
Maestro Matemático Grupo: Usuario FMAT Mensajes: 100 Registrado: 17-April 11 Miembro Nº: 87.227 Nacionalidad: Colegio/Liceo: Universidad: Sexo:	Una solucion un poco mas generalizada del P6 $TEX: Primero multiplicamos la primera expresión por 1995 nos quedaría lo siguiente$ $TEX: $$\frac{1995^{1995}+1995}{1995^{1996}+1995}$$$ $TEX: $$a=1995^{1995}$$$ $TEX: $$b=1995^{1996}$$$ $TEX: Ahora también tenemos que$ $TEX: $$b>a>0$$$ $TEX: y$ $TEX: $$x>c>0$$$ $TEX: , para la siguiente expresión:$ $TEX: $$\frac{a+x}{b+x}$$$ $TEX: y$ $TEX: $$\frac{a+c}{b+c}$$$ $TEX: (1)$ $TEX: $$b + c>a +c$$$ $TEX: (2)$ $TEX: $$b + x>a + x$$$ $TEX: (1)<img src="style_emoticons/default/sad.gif" style="vertical-align:middle" emoid=":(" border="0" alt="sad.gif" />2), notamos que no tendremos problemas con las desigualdades al multiplicar o dividir por que todo es positivo$ $TEX: $$\frac{a+x}{b+x}>\frac{a+c}{b+c}$$$ $TEX: Por lo tanto la primera expresión es mayor que la segunda$ --------------------

« Posterior · Olimpiada Nacional · Anterior »

2 Páginas:

1 2 >

Reply to this topic

Start new topic

1 usuario(s) está(n) leyendo esta discusión (1 invitado(s) y 0 usuario(s) anónimo(s))

0 miembro(s):

Modo de Ver: Estándar · Cambiar a: Lineal+ · Cambiar a: Outline

Suscribirse · Enviar por correo · Imprimir · Suscribirse a este foro

Versión Lo-Fi

Fecha y Hora actual: 2nd April 2025 - 02:25 AM

Powered By IP.Board 2.2.1 © 2007 IPS, Inc.