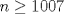|
|
|
|
|
|
|
  |
 Apr 19 2011, 12:23 PM Apr 19 2011, 12:23 PM
Publicado:
#1
|
|
 Dios Matemático Supremo Grupo: Administrador Mensajes: 2.706 Registrado: 13-May 05 Desde: Santiago de Chile Miembro Nº: 10 Nacionalidad:  Colegio/Liceo:  Sexo:  |
IX CAMPEONATO ESCOLAR DE MATEMÁTICA - CMAT Fecha 1: Sábado 16 de Abril de 2011 Cuarto Nivel Individual Problema 1 Se tiene un tablero cuadriculado con 2011 filas y 2011 columnas, al cual se le ha retirado la casilla central. Se dispone también de una gran cantidad de fichas con forma de rectángulo de dimensiones 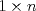 (cada ficha cubre exactamente (cada ficha cubre exactamente  casillas). El objetivo es cubrir este "tablero" usando estas fichas, sin superponerlas y sin salir de los límites del "tablero" casillas). El objetivo es cubrir este "tablero" usando estas fichas, sin superponerlas y sin salir de los límites del "tablero"
¿Cuántos triángulos se pueden construir con sus tres vértices en el retículo de la figura?  -------------------- |
|
|
|
  |
1 usuario(s) está(n) leyendo esta discusión (1 invitado(s) y 0 usuario(s) anónimo(s))
0 miembro(s):
| Versión Lo-Fi | Fecha y Hora actual: 16th April 2025 - 07:13 PM |





 (describa cómo ubicar las fichas)
(describa cómo ubicar las fichas)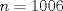 (describa cómo ubicar las fichas)
(describa cómo ubicar las fichas)