Prueba Final (1993), Sin solución: 1,2,3,4,5,6,7 Opciones

[Newtype]

Problema 4: En un cierto club, cada miembro está en dos comisiones. Además, se sabe que dos comisiones cualesquiera siempre tienen exactamente un miembro en común. Sabiendo que hay cinco comisiones, ¿Cuántos miembros tiene el club?

Léase como tabla:
Club
1 A B C D
2 A E F G
3 B E H I
4 C F H J
5 D G I J

Explico: La primera comisión, debe compartir 1 miembro con cada una de las otras, así, repartimos los miembros entre las demás, uno en cada una...las letras representan a un cierto miembro. Luego, vamos repartiendo nuevas letras, primero en una comisión, luego en la siguiente (así, aparece E y liuego en la tercera fila también E), para el siguiente, ocupamos la subsiguiente comisión, así, hasta completar la nueva fila y que comparta un miembro con cada una de las filas siguientes (con la anterior, ya se cumple, por este mismo algoritmo).

Luego, ya que A,B,...,J son 10 letras, el club tiene 10 miembros.

Saludos!

[Newtype]

Problema 5: Sean 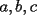tres números positivos menores que 1. Pruebe que no pueden ocurrir simultáneamente las tres desigualdades:

i)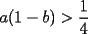
ii)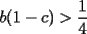
iii)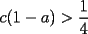

Asumamos, por el contrario, que sí se pudieran cumplir al mismo tiempo...entonces, en I) como b es menor que 1, ambos factores son positivos, así, podemos aplicar la raíz cuadrada a esta desigualdad, pues ambos miembros son positivos. Luego, hacemos AM-GM: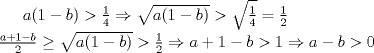

Si hacemos lo mismo con las otras 2 desigualdades, y las sumamos, queda: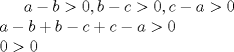

Que es falso, así que lo que inicialmente asumimos era falso. Contradicción.

[Newtype]

Problema 7: Seis jóvenes que asistieron a una reunión vistiendo chalecos de distintos colores, decidieron intercambiarlos y salieron vistiendo todos de color diferente a aquel con que llegaron. El chaleco con que salió Antonio pertenecía al joven que salió con el chaleco de Bernardo. El dueño del chaleco con que salió Carlos, salió con el chaleco que pertenecía al joven que se llevó el de Diego. Quien se llevó el chaleco de Eduardo no era el dueño del que se llevó Francisco. Determine quién salió con el chaleco de Antonio, y quién es el dueño del chaleco que se llevó Antonio.

Después de cierto tiempo pensando, trazando "flechas" y con una pizca de suerte, he llegado a la siguiente confromación, que al parecer, cumple con lo pedido: (no sé si haya más...)
Cada letra es la priemra del nombre del joven.

La flecha apunta hacia quien se le entregó´el chaleco

A->B->F->A D->E->C->D

Luego, Bernardo se llevó el chaleco de Antonio, que a la vez, se llevó el chaleco que le pertenece a Francisco.

Saludos!

[S. E. Puelma Moy...]

Está correcto. Aunque uno debe estar atento a que todos los factores que allí aparecen: a, b, c, 1-a, 1-b, 1-c son positivos. Esto es especialmente importante al momento de multiplicar o dividir desigualdades, por un asunto de signos.

La solución de Hamon (mensaje #12) también es correcta.