|
|
|
|
|
|
|
  |
 Feb 26 2007, 02:30 PM Feb 26 2007, 02:30 PM
Publicado:
#1
|
|
 Dios Matemático Supremo Grupo: Usuario FMAT Mensajes: 558 Registrado: 14-May 05 Desde: Maipú, Stgo, Chile Miembro Nº: 27 Nacionalidad:  Colegio/Liceo:  Universidad:  Sexo:  |
15ª OLIMPIADA NACIONAL DE MATEMÁTICAS Prueba de Clasificación, Nivel Mayor Primera Prueba Problema 1: Los puntos 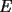 y y 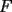 dividen los lados dividen los lados 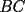 y y 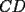 del cuadrilátero convexo del cuadrilátero convexo 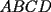 en dos partes iguales. Además, los segmentos en dos partes iguales. Además, los segmentos 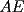 , , 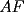 y y 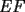 dividen el cuadrilátero en 4 triángulos, donde sus áreas coinciden con 4 números enteros consecutivos. Determine la mayor área posible que puede tener el triángulo dividen el cuadrilátero en 4 triángulos, donde sus áreas coinciden con 4 números enteros consecutivos. Determine la mayor área posible que puede tener el triángulo 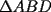 . . Problema 2: Encuentre todas las soluciones del sistena de inecuaciones: 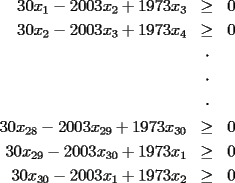 Problema 3: Se define una sucesión 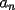 por: por: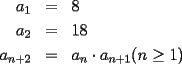 Determine los valores de  para los cuales para los cuales 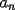 es un cuadrado perfecto. es un cuadrado perfecto.Segunda Prueba Problema 4: La familia de Maca tiene 4 personas: el abuelo, la mamá, el papá y ella misma. Si se duplicara el tamaño de la beca mensual que recibe Maca, los ingresos de la familia aumentarían en 5 por ciento. Si en lugar de la beca de Maca, se duplicara el sueldo de su mamá,los ingresos familiares crecen en un 15 por ciento. El mismo procedimiento da 25 por ciento en el caso del papá. ahora, ¿En qué porcentaje crece el ingreso familiar, si sólo se duplica el sueldo del abuelo? Problema 5: Tres números positivos 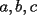 satisfacen la igualdad satisfacen la igualdad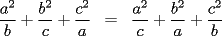 Pruebe que al menos dos de los valores son iguales. Problema 6: Calcule el área de la región comprendida entre los tres semicírculos, sabiendo que 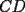 es perpendicular a es perpendicular a 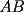 y que y que 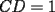 . . screen.width*0.6) {this.resized=true; this.width=screen.width*0.4; this.alt='Pincha Aqui para ver esta imagen en su tamaño original';}" onmouseover="if(this.resized) this.style.cursor='hand';" onclick="if(this.resized) {window.open('http://img118.imageshack.us/img118/4218/2004meqs5.jpg');}" /> screen.width*0.6) {this.resized=true; this.width=screen.width*0.4; this.alt='Pincha Aqui para ver esta imagen en su tamaño original';}" onmouseover="if(this.resized) this.style.cursor='hand';" onclick="if(this.resized) {window.open('http://img118.imageshack.us/img118/4218/2004meqs5.jpg');}" />-------------------- El peor defecto del ignorante es que ignora su propia ignorancia................
|
|
|
|
 Aug 8 2007, 04:52 PM Aug 8 2007, 04:52 PM
Publicado:
#2
|
|
|
Dios Matemático Supremo Grupo: Usuario FMAT Mensajes: 878 Registrado: 14-May 07 Desde: Talcahuano Miembro Nº: 5.845 Nacionalidad:  Colegio/Liceo:  Sexo:  |
Sol al P6.
Sean 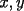 , los radios del , los radios del 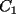 y el y el 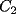 , respectivamente. , respectivamente.Por el enunciado se sabe que 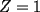 Como el triangulo 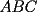 es rectángulo en es rectángulo en 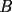 y y 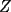 es perpendicular a es perpendicular a 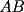 podemos usar el teorema de euclides y decir: podemos usar el teorema de euclides y decir: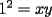 de donde se saca que de donde se saca que 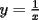 . .El Área del semicírculo grande 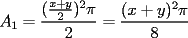 , pero como , pero como 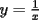 , entonces reemplazando tenemos que , entonces reemplazando tenemos que 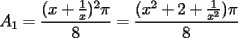 . .La suma de las Áreas de los circulos mas pequeños 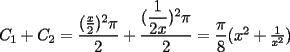 Ahora podemos calcular el área buscada, restandole las áreas de los círculos pequeños al círculo grande. 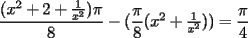
Archivo(s) Adjunto(s)
--------------------  |
|
|
|
 Aug 8 2007, 04:59 PM Aug 8 2007, 04:59 PM
Publicado:
#3
|
|
 Staff FMAT Grupo: Super Moderador Mensajes: 8.124 Registrado: 21-May 06 Miembro Nº: 1.156 Nacionalidad:  Sexo:  |
Hola
La región comprendida entre los tres semicírculos también es denominada "Arbelos" ó "Cuchillo del zapatero", y ésta en efecto tiene su área equivalente a la del círculo cuyo diámetro es CD. Así 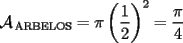 Lo que acabaste de hacer fue practicamente demostrar esa formulita |
|
|
|
 Aug 15 2007, 11:41 AM Aug 15 2007, 11:41 AM
Publicado:
#4
|
|
 Dios Matemático Supremo Grupo: Administrador Mensajes: 2.706 Registrado: 13-May 05 Desde: Santiago de Chile Miembro Nº: 10 Nacionalidad:  Colegio/Liceo:  Sexo:  |
Mirando con cuidado, uno ve que la definición de "x" e "y" son como los diámetros de dichas circunferencias (así lo usaste en tu argumento). Ese pequeño comentario, junto con el hecho que podías trabajar con "y" en vez de "1/x" (fíjate que la escritura del código LateX y la presentación de la solución, mejoran con esta observación)
Saludos -------------------- |
|
|
|
 Aug 16 2007, 05:33 PM Aug 16 2007, 05:33 PM
Publicado:
#5
|
|
|
Dios Matemático Supremo Grupo: Usuario FMAT Mensajes: 878 Registrado: 14-May 07 Desde: Talcahuano Miembro Nº: 5.845 Nacionalidad:  Colegio/Liceo:  Sexo:  |
tienes toda la razon sebastian, ahi
 e e 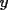 deben ser diametros, gracias por la observacion. deben ser diametros, gracias por la observacion.Bueno tengo la respuesta al P5. 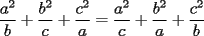 / todo por abc. / todo por abc.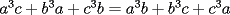 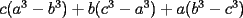 / claramente si / claramente si 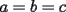 esto se cumple, pero si solo esto se cumple, pero si solo 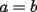 ... ...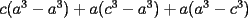 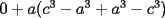 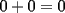 Analogamente se puede hacer con los 3 valores y siempre dara 0. --------------------  |
|
|
|
 Aug 17 2007, 11:11 AM Aug 17 2007, 11:11 AM
Publicado:
#6
|
|
 Dios Matemático Supremo Grupo: Administrador Mensajes: 2.706 Registrado: 13-May 05 Desde: Santiago de Chile Miembro Nº: 10 Nacionalidad:  Colegio/Liceo:  Sexo:  |
tienes toda la razon sebastian, ahi  e e 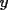 deben ser diametros, gracias por la observacion. deben ser diametros, gracias por la observacion.Bueno tengo la respuesta al P5. 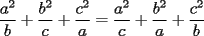 / todo por abc. / todo por abc.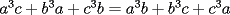 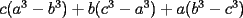 / claramente si / claramente si 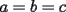 esto se cumple, pero si solo esto se cumple, pero si solo 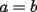 ... ...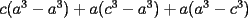 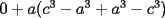 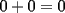 Analogamente se puede hacer con los 3 valores y siempre dara 0. Estás demostrando cosas del siguiente tipo (análogamente, para una de las igualdades a=c, b=c de hipótesis): 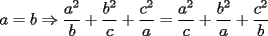 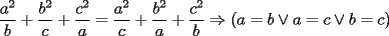 -------------------- |
|
|
|
 Sep 20 2007, 11:54 PM Sep 20 2007, 11:54 PM
Publicado:
#7
|
|
 Dios Matemático Supremo Grupo: Colaborador Gold Mensajes: 1.118 Registrado: 11-September 05 Desde: Valdivia/Ancud Miembro Nº: 302 Nacionalidad:  Colegio/Liceo:  Universidad:  Sexo:  |
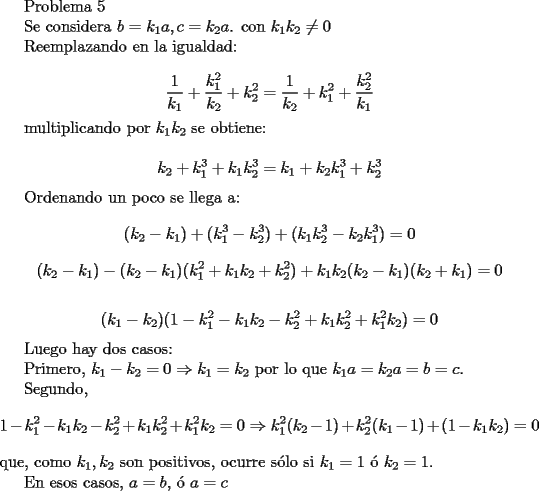
Mensaje modificado por JoNy_SaTiE el Sep 21 2007, 02:38 PM -------------------- Comienza a crear documentos con LaTeX.
Ya usas LaTeX y quieres aprender un poco más ... pincha aquí Si eres de la UaCH ... únete a la causa !!! J. Jonathan H. Oberreuter A. Universidad Austral de Chile - RWTH Aachen alumni Est. Magister en Acústica y Vibraciones Ingeniero Civil Acústico (E) Bachiller y Licenciado en Cs. de la Ingeniería |
|
|
|
 Sep 21 2007, 11:56 AM Sep 21 2007, 11:56 AM
Publicado:
#8
|
|
 Dios Matemático Supremo Grupo: Administrador Mensajes: 2.706 Registrado: 13-May 05 Desde: Santiago de Chile Miembro Nº: 10 Nacionalidad:  Colegio/Liceo:  Sexo:  |
Tienes que corregir un error de tipeo en la primera línea (c=k2a, en vez de c=k2c). El error más importante para corregir, está después del "ordenando un poco" (las agrupaciones no las hiciste muy bien, porque si desarrollas la factorización, aparecen términos de grado 4). Finalmente, si el producto de dos números es igual a 0, no puedes deducir que el primer factor sea nulo, a menos que compruebes que el otro factor no lo es
-------------------- |
|
|
|
 Sep 21 2007, 01:07 PM Sep 21 2007, 01:07 PM
Publicado:
#9
|
|
 Dios Matemático Supremo Grupo: Colaborador Gold Mensajes: 1.118 Registrado: 11-September 05 Desde: Valdivia/Ancud Miembro Nº: 302 Nacionalidad:  Colegio/Liceo:  Universidad:  Sexo:  |
Sí, evidentemente había un error en la factorización que ya está rreglado, lo mismo con lo del principio. Ahora creo que falta argumentar más el segunda caso final.
-------------------- Comienza a crear documentos con LaTeX.
Ya usas LaTeX y quieres aprender un poco más ... pincha aquí Si eres de la UaCH ... únete a la causa !!! J. Jonathan H. Oberreuter A. Universidad Austral de Chile - RWTH Aachen alumni Est. Magister en Acústica y Vibraciones Ingeniero Civil Acústico (E) Bachiller y Licenciado en Cs. de la Ingeniería |
|
|
|
 Sep 21 2007, 01:28 PM Sep 21 2007, 01:28 PM
Publicado:
#10
|
|
 Dios Matemático Supremo Grupo: Administrador Mensajes: 2.706 Registrado: 13-May 05 Desde: Santiago de Chile Miembro Nº: 10 Nacionalidad:  Colegio/Liceo:  Sexo:  |
Ahora, el error se encuentra en la última factorización (cuando trabajas con el segundo caso)... por otro lado, no veo por qué puedes concluir tan rápido que k1=1 o k2=1... tal vez sí, si trabajásemos con números naturales, pero este no es el caso
PD: existe otra solución... -------------------- |
|
|
|
  |
1 usuario(s) está(n) leyendo esta discusión (1 invitado(s) y 0 usuario(s) anónimo(s))
0 miembro(s):
| Versión Lo-Fi | Fecha y Hora actual: 2nd April 2025 - 02:25 AM |











