I1 Geometria I (Mat1305) - Foro fmat.cl

Portal Matemático

¿Qué es FMAT?

Foro fmat.cl > Programa Enseñanza Universitaria > Comunidades Universitarias > Universidad Católica > Geometría

Reply to this topic

Start new topic

I1 Geometria I (Mat1305)

Plumifero Ver Perfil del Miembro Ver los mensajes de este miembro	Apr 13 2011, 05:32 PM Publicado: #1
Dios Matemático Supremo Grupo: Usuario FMAT Mensajes: 545 Registrado: 30-March 08 Miembro Nº: 18.446	Interrogracion N°1 Geometria - MAT1305 $TEX: <br /><br />\noindent 1) Demuestre que para todo $\alpha \in R$ tal que $cos\alpha$, $cos2\alpha$, $cos3\alpha \ne 0$ se tiene: \\<br /><br />$tg3\alpha-tg2\alpha-tg\alpha=tg\alpha\cdot tg2\alpha\cdot tg3\alpha$ \\<br /><br />\noindent 2)Encuentre los valores de $x$ tales que: \\<br /><br />$2Arccot2+Arccos\dfrac{3}{5}=Arccscx$ \\<br /><br />\noindent 3) En un triangulo $ABC$ cualquiera, considere un punto $D$ en el lado $CB$ tal que: \\<br /><br />$\|CD\|=\dfrac{a}{3}$ \\<br /><br />Encuentre una formula para el largo $x=\|AD\|$ en terminos de $a$,$b$,$c$. \\<br /><br />\noindent 4)Demuestre que si en un triangulo $ABC$ se cumple que: \\<br /><br />$acos\beta+bcos\gamma+ccos\alpha=\dfrac{a+b+c}{2}$ \\<br /><br />entonces el traingulo es isosceles.<br />$ Mensaje modificado por Plumifero el Apr 13 2011, 05:39 PM

~Fatal_Collapse~ Ver Perfil del Miembro Ver los mensajes de este miembro	Apr 16 2011, 05:21 PM Publicado: #2
Dios Matemático Supremo Grupo: Usuario FMAT Mensajes: 1.564 Registrado: 12-November 07 Desde: La Union, XIV Region de los Rios Miembro Nº: 12.607 Nacionalidad: Colegio/Liceo: Universidad: Sexo:	CITA(Plumifero @ Apr 13 2011, 06:32 PM) $TEX: Demuestre que si en un triangulo $ABC$ se cumple que: \\<br /><br />$acos\beta+bcos\gamma+ccos\alpha=\dfrac{a+b+c}{2}$ \\<br /><br />entonces el traingulo es isosceles.<br />$ Esta es la solución "feita" que se me ocurrió en el momento que di la I, distinta a la expuesta en el 103 Trigonometry Problems. Por el Teorema del Coseno, tenemos que 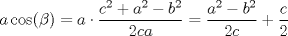$TEX: $a\cos(\beta)=a\cdot\dfrac{c^2+a^2-b^2}{2ca}=\dfrac{a^2-b^2}{2c}+\dfrac{c}{2}$$ . 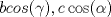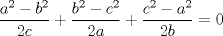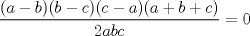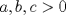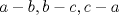Procediendo del mismo modo con $TEX: $bcos(\gamma), c\cos(\alpha)$$ , obtenemos que la igualdad de la hipótesis es equivalente a $TEX: $\dfrac{a^2-b^2}{2c}+\dfrac{b^2-c^2}{2a}+\dfrac{c^2-a^2}{2b}=0$$ Pero a su vez esta equivale a que $TEX: $\dfrac{(a-b)(b-c)(c-a)(a+b+c)}{2abc}=0$$ Como $TEX: $a,b,c>0$$ , su suma lo es, por lo tanto uno de los factores $TEX: $a-b, b-c,c-a$$ debe ser nulo, demostrando que el triángulo es isósceles. Saludos Wenas don Plumífero... -------------------- Ricardo Vargas Obando Ex-alumno Deutsche Schule La Unión (Generación 2010, de los 150 años). Novato de Licenciatura en Matemática/Estadística, en la Pontificia Universidad Católica de Chile. Grupo de facebook de Novatos Matemática y Estadística PUC 2011 Currículum Olímpico: Medalla de Plata, XIX Olimpiada Nacional de Matemática Nivel Menor (2007) Medalla de Oro, XXI Olimpiada Nacional de Matemática Nivel Mayor (2009) Medalla de Bronce, XXV Olimpiada Iberoamericana de Matemática (2010) Medalla de Oro, XXII Olimpiada Nacional de Matemática Nivel Mayor (2010) "What we learned as children, that one plus one equals two, we know to be false. One plus one equals one. We even have a word when you plus another, equals one. That word is love." "Todos piensan en cambiar el mundo, pero nadie piensa en cambiarse a sí mismo."

Plumifero Ver Perfil del Miembro Ver los mensajes de este miembro	Apr 16 2011, 07:44 PM Publicado: #3
Dios Matemático Supremo Grupo: Usuario FMAT Mensajes: 545 Registrado: 30-March 08 Miembro Nº: 18.446	1) $TEX: <br />\noindent Se tiene que $tg3\alpha-tg2\alpha-tg\alpha=\dfrac{sen3\alpha cos2\alpha cos\alpha-sen2\alpha cos3\alpha cos\alpha-sen\alpha cos3\alpha cos2\alpha}{cos3\alpha cos2\alpha cos\alpha}$ \\ \\<br /><br />\noindent pero\\ \\ $sen3\alpha cos2\alpha cos\alpha-sen2\alpha cos3\alpha cos\alpha-sen\alpha cos3\alpha cos2\alpha\\=cos\alpha(sen3\alpha cos2\alpha-sen2\alpha cos3\alpha)-sen\alpha cos3\alpha cos2\alpha$\\=$cos\alpha sen\alpha -sen\alpha cos3\alpha cos2\alpha=sen\alpha(cos\alpha-cos3\alpha cos2\alpha)$ \\<br /><br />\noindent como, $cos\alpha=cos(3\alpha-2\alpha)=cos3\alpha cos2\alpha+sen3\alpha sen2\alpha$ \\<br /><br />\noindent se tiene que, $sen\alpha(cos\alpha-cos3\alpha cos2\alpha)=sen\alpha sen2\alpha sen3\alpha$ \\<br /><br />\noindent de esto se concluye que $tg3\alpha-tg2\alpha-tg\alpha=tg3\alpha\cdot tg2\alpha \cdot tg\alpha$<br /><br /><br />$ Saludos fatal

El Geek Ver Perfil del Miembro Ver los mensajes de este miembro	Apr 18 2011, 04:42 PM Publicado: #4
Dios Matemático Supremo Grupo: Usuario FMAT Mensajes: 2.818 Registrado: 3-October 09 Miembro Nº: 59.773 Nacionalidad: Colegio/Liceo: Universidad: Sexo:	. Mensaje modificado por El Geek el Apr 19 2011, 10:33 AM -------------------- Me voy, me jui.

El Geek Ver Perfil del Miembro Ver los mensajes de este miembro	Apr 19 2011, 10:33 AM Publicado: #5
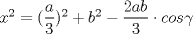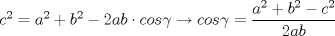Dios Matemático Supremo Grupo: Usuario FMAT Mensajes: 2.818 Registrado: 3-October 09 Miembro Nº: 59.773 Nacionalidad: Colegio/Liceo: Universidad: Sexo:	A ver, me voy a tirar al agua con el p3 Por teorema de coseno tenemos que $TEX: $x^2=(\dfrac{a}{3})^2+b^2-\dfrac{2ab}{3}\cdot cos\gamma$$ , pero $TEX: $c^2=a^2+b^2-2ab\cdot cos\gamma \rightarrow cos\gamma=\dfrac{a^2+b^2-c^2}{2ab}$$ . Entonces reemplazando nos queda: $TEX: \[x = \frac{{\sqrt {{3c^2} + 6{b^2} - {2a^2}} }}{3}\]$ Saludos PD: el desarrollo $TEX: \[\begin{array}{l}<br />{x^2} = {\left( {\frac{a}{3}} \right)^2} + {b^2} - \frac{{2ab}}{3} \cdot \frac{{{a^2} + {b^2} - {c^2}}}{{2ab}}\\<br />{x^2} = \frac{{{a^2}}}{9} + \frac{{3{b^2} - {a^2} - {b^2} + {c^2}}}{3}\\<br />{x^2} = \frac{{ - {2a^2} + 6{b^2} + {3c^2}}}{9}<br />\end{array}\]$ Wena cabros Mensaje modificado por El Geek el Apr 20 2011, 01:49 AM -------------------- Me voy, me jui.

gamby Ver Perfil del Miembro Ver los mensajes de este miembro	May 19 2011, 03:34 AM Publicado: #6
Dios Matemático Supremo Grupo: Usuario FMAT Mensajes: 2.847 Registrado: 3-October 09 Miembro Nº: 59.760 Nacionalidad: Colegio/Liceo: Universidad: Sexo:	otra solucion p1 Se sabe que 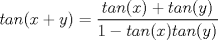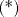$TEX: $tan(x+y)= \dfrac{tan(x)+tan(y)}{1-tan(x)tan(y)}$$ $TEX: ()$ ordenando convenientemente 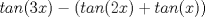$TEX: $tan(3x) -\left (tan(2x)+tan(x)\right) $$ y por 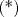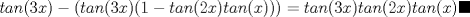$TEX: ()$ $TEX: $tan(3x)-\left( tan(3x)(1-tan(2x)tan(x)) \right) = tan(3x)tan(2x)tan(x) \blacksquare $$

« Posterior · Geometría · Anterior »

Reply to this topic

Start new topic

1 usuario(s) está(n) leyendo esta discusión (1 invitado(s) y 0 usuario(s) anónimo(s))

0 miembro(s):

Modo de Ver: Estándar · Cambiar a: Lineal+ · Cambiar a: Outline

Suscribirse · Enviar por correo · Imprimir · Suscribirse a este foro

Versión Lo-Fi

Fecha y Hora actual: 4th April 2025 - 04:57 AM

Powered By IP.Board 2.2.1 © 2007 IPS, Inc.