Prueba de Clasificación, Nivel Mayor (2002)

2 Páginas:

< 1 2

Prueba de Clasificación, Nivel Mayor (2002), Sin solución: 1,2,3,4,5,6,7

Pedantic Anarchy... Pedantic Anarchy Ver Perfil del Miembro Ver los mensajes de este miembro	Jul 9 2010, 10:05 PM Publicado: #11
Dios Matemático Supremo Grupo: Usuario FMAT Mensajes: 688 Registrado: 8-November 09 Desde: Villarrica Miembro Nº: 61.657 Nacionalidad: Colegio/Liceo: Universidad: Sexo:	CITA(Hamon @ Jul 9 2010, 10:56 PM) Tomemos 3 puntos al interior del cuadrado ABCD de lado a, P,Q,R. Luego, es fácil ver que el área del triángulo se maximizará cunado tenga máxma base y altura, por lo que P y Q deben coincidir con 2 vértices del cuadrado, y R estar en el lado opuesto a estos. Finalmente, este triángulo tendrá área correspondiente a la mitad del área del cuadrado. Luego, queda demostrado que no pueden tomarse 3 puntos al interior de un cuadrado tal que formen un triángulo de área mayor a la mitad del área del cuadrado. (Más formalmente hay un método con desigualdades que demuestra los lugares de P,Q y R tales que el área del triángulo mencionado se maximice, queda a cargo del lector, ya que es bastante intuitivo) Saludos! Esta claro, pero demostrar lo que resulta intuitivo era la gracia del problema. Lo del deja vu lo digo por que es practicamente igual al P2 de la final nacional nivel menor de este año -------------------- yo no soy especial a pesar que ella lo dijo tengo unos krk y un celular hechizo aún vácilo SFDK en el segundo piso y la frase final da igual la improviso

snw Ver Perfil del Miembro Ver los mensajes de este miembro	Aug 9 2010, 06:38 PM Publicado: #12
Dios Matemático Supremo Grupo: Usuario FMAT Mensajes: 2.139 Registrado: 11-June 08 Desde: UK Miembro Nº: 26.837 Nacionalidad: Colegio/Liceo: Universidad: Sexo:	Sea un triangulo AEF interior al cuadrado, supongamos sin perdida de generalidad que el vertice A esta ubicado en un vertice del cuadrado (esto pues al tener un vertice en otro lugar se puede extender a una arista del cuadrado lo que claramente mayora el area, y ponerlo en un vertice del cuadrado pues el modo de resolucion seria analogo a si estuviera en una arista). 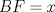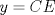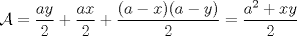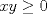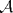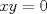Consideremos la siguiente figura Si denotadmos $TEX: $BF=x$$ e $TEX: $y=CE$$ notamos que el area exterior al triangulo está dada por $TEX: $\mathcal{A}=\dfrac{ay}{2}+\dfrac{ax}{2}+\dfrac{(a-x)(a-y)}{2}=\dfrac{a^2+xy}{2}$$ Como $TEX: $xy\ge 0$$ , el problema es equivalente a minimizar $TEX: $\mathcal{A}$$ que se soluciona cuando $TEX: $xy=0$$ probando lo pedido. saludos -------------------- blep

Profesorx Ver Perfil del Miembro Ver los mensajes de este miembro	Aug 9 2010, 10:38 PM Publicado: #13
Principiante Matemático Grupo: Usuario FMAT Mensajes: 5 Registrado: 9-September 09 Miembro Nº: 58.558 Nacionalidad: Colegio/Liceo: Universidad: Sexo:	P1. Es como pregunta de ingenio más que de olimpiada (o estaré demasiado perdido). Obviamente hay más té en la leche. El secreto está en la primera cucharada, compuesta íntegramente por té. Las cucharadas restantes contienen mezclas por lo que se podría decir que ninguna otra cucharada pordría equiparar el aporte del té a la leche de la primera. Eso sería Cuek Saludos.

Emi_C Ver Perfil del Miembro Ver los mensajes de este miembro	Aug 10 2010, 07:08 PM Publicado: #14
Dios Matemático Grupo: Usuario FMAT Mensajes: 234 Registrado: 5-April 10 Desde: Arg Miembro Nº: 67.793 Nacionalidad: Sexo:	CITA(Hamon @ Jul 9 2010, 10:56 PM) Tomemos 3 puntos al interior del cuadrado ABCD de lado a, P,Q,R. Luego, es fácil ver que el área del triángulo se maximizará cunado tenga máxma base y altura, por lo que P y Q deben coincidir con 2 vértices del cuadrado, y R estar en el lado opuesto a estos. Finalmente, este triángulo tendrá área correspondiente a la mitad del área del cuadrado. Luego, queda demostrado que no pueden tomarse 3 puntos al interior de un cuadrado tal que formen un triángulo de área mayor a la mitad del área del cuadrado. (Más formalmente hay un método con desigualdades que demuestra los lugares de P,Q y R tales que el área del triángulo mencionado se maximice, queda a cargo del lector, ya que es bastante intuitivo) Saludos! Yo una vez creo q lo pense, no se como a ese problema, y use esa idea, no es muy dificil de demostrar eso que pones cm trivial o conocido, esta buena la idea, a darle -------------------- $TEX: $\sqrt{a \cdot b} \le \frac{a+b}{2}$$

Newtype Ver Perfil del Miembro Ver los mensajes de este miembro	Aug 10 2010, 07:28 PM Publicado: #15
Dios Matemático Supremo Grupo: Team Ensayos FMAT Mensajes: 1.559 Registrado: 18-November 07 Miembro Nº: 12.754 Nacionalidad: Sexo:	CITA(Emi_C @ Aug 10 2010, 08:08 PM) Yo una vez creo q lo pense, no se como a ese problema, y use esa idea, no es muy dificil de demostrar eso que pones cm trivial o conocido, esta buena la idea, a darle no tranki si lo demostre, creo haber puesto "es facil demostrarlo" XD...y sino, lo digo ahora que lo haga otro -------------------- Empezando con Desigualdades? Encuentra aquí problemas resueltos

mamboraper Ver Perfil del Miembro Ver los mensajes de este miembro	Apr 29 2021, 08:31 PM Publicado: #16
Maestro Matemático Grupo: Usuario FMAT Mensajes: 134 Registrado: 28-March 14 Miembro Nº: 128.100 Nacionalidad: Sexo:	3. $TEX: El enunciado original del problema dice que los $(a_n)$ son enteros.\\ <br />Supongamos que existe una secuencia $(a_n)$ de enteros cumpliendo i) y ii). Llamemos $S_n := a_{n+1}+...+a_{n+2002}$ y $P_n := a_1+...+a_{2002n+1}$, tenemos que $S_n>0$ para todo $n\geq 1$ entonces $S_n\geq 1$, pues $S_n\in\mathbb{Z}$, y por la misma razón $P_n\leq -1$ pues $P_n<0$. Es fácil chequear que si $N\in\mathbb{N}\setminus\{0\}$: $$ P_N = a_1+\sum_{n=0}^{N-1} S_{2002\cdot n +1} $$ De acá se sigue que $$-1\geq P_N=a_1+\sum_{n=0}^{N-1} S_{2002\cdot n +1} \geq a_1+\sum_{n=0}^{N-1}1 = a_1+N$$ y entonces $a_1\leq -(N+1)$ para todo $N\geq 1$, pero como $a_1\in\mathbb{Z}$, tomamos $N=\|a_1\|$ y llegamos a una contradicción. Luego no puede existir una secuencia con tales características.$ Mensaje modificado por mamboraper el Apr 30 2021, 12:21 AM -------------------- Hago clases particulares (activo 2024). Cualquier consulta por MP.

2 Páginas:

< 1 2

1 usuario(s) está(n) leyendo esta discusión (1 invitado(s) y 0 usuario(s) anónimo(s))

0 miembro(s):

Modo de Ver: Estándar · Cambiar a: Lineal+ · Cambiar a: Outline

Fecha y Hora actual: 23rd November 2024 - 05:30 PM