|
|
|
|
|
|
|
  |
 Feb 26 2007, 02:25 AM Feb 26 2007, 02:25 AM
Publicado:
#1
|
|
 Dios Matemático Supremo Grupo: Usuario FMAT Mensajes: 558 Registrado: 14-May 05 Desde: Maipú, Stgo, Chile Miembro Nº: 27 Nacionalidad:  Colegio/Liceo:  Universidad:  Sexo:  |
14ª OLIMPIADA NACIONAL DE MATEMÁTICAS Prueba de Clasificación, Nivel Mayor Primera Prueba Problema 1: Sergio tiene a su disposición un jarro que contiene dos litro de té y un jarro que contiene dos litros de leche. Sergio toma un vaso gradudado y retira 50 cm³ de té y lo coloca en el jarro con leche. Luego de revolver el contenido, Saca 50 cm³ de la mezcla y lo coloca en el jarro que contiene té. Luego de estas operaciones, ¿Hay más té en el jarro de leche o hay las leche en el jarro de té?. Problema 2: Pruebe que no es posible construir un triángulo de área mayor a 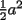 dentro de un cuadrado de lado dentro de un cuadrado de lado  . .Problema 3: Pruebe que no existe una sucesión 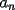 tal que cumpla simultáneamente: tal que cumpla simultáneamente:i) 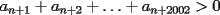 para todo natural para todo natural  . .ii) 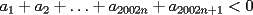 para todo natural para todo natural  . .Segunda Prueba Problema 4: Se organiza una fiesta de matrimonios para el día de los enamorados. Se reúnen 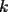 parejas. El dueño de casa nota que cada persona, distinta de él, saludó a un número distinto de participantes. Si una persona no se saluda a sí misma ni a su cónyuge, pruebe que el dueño de casa saludó a la mitad de los invitados. (En particular, es un mal educado y su mujer también.). parejas. El dueño de casa nota que cada persona, distinta de él, saludó a un número distinto de participantes. Si una persona no se saluda a sí misma ni a su cónyuge, pruebe que el dueño de casa saludó a la mitad de los invitados. (En particular, es un mal educado y su mujer también.).Problema 5: El número 3 tiene las siguientes representaciones como suma de números positivos: 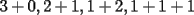 , considerando importante el orden en que se suma,excepto en el caso del 3. Mostrar que cualquier número entero positivo $n$ se puede expresar de , considerando importante el orden en que se suma,excepto en el caso del 3. Mostrar que cualquier número entero positivo $n$ se puede expresar de 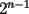 formas distintas con estas consideraciones de orden. formas distintas con estas consideraciones de orden.Problema 6: Consideramos un tablero de ajedrez de 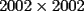 casillas. Se colocan 100.000 torres en el tablero. Dos torres se dicen vecinas si están en la misma vertical u horizontal y no hay otra torre entre ellas. Pruebe que se pueden pintar las 100.000 torres usando tres colores de tal forma que dos torres vecinas no se pintan del mismo color. casillas. Se colocan 100.000 torres en el tablero. Dos torres se dicen vecinas si están en la misma vertical u horizontal y no hay otra torre entre ellas. Pruebe que se pueden pintar las 100.000 torres usando tres colores de tal forma que dos torres vecinas no se pintan del mismo color. Problema 7: Sea 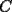 una circunferencia, pruebe que el polígono de una circunferencia, pruebe que el polígono de  lados inscrito en lados inscrito en 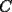 con mayor área es un polígono regular. Sugerencia: Trate primero el caso con mayor área es un polígono regular. Sugerencia: Trate primero el caso 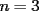 , luego , luego 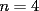 y por último concluya en general. y por último concluya en general.
-------------------- El peor defecto del ignorante es que ignora su propia ignorancia................
|
|
|
|
 Aug 5 2007, 09:14 PM Aug 5 2007, 09:14 PM
Publicado:
#2
|
|
|
Dios Matemático Supremo Grupo: Usuario FMAT Mensajes: 878 Registrado: 14-May 07 Desde: Talcahuano Miembro Nº: 5.845 Nacionalidad:  Colegio/Liceo:  Sexo:  |
P2=
Bueno existen 2 casos para que el area del triangulo Dentro de un cuadrado de lado  sea la máxima: sea la máxima:Caso 1) La base es igual a la diagonal, que para que tenga area maxima, la altura debe ser igual a la la mitad de la otra diagonal ( que en el fondo mide lo mismo que la mitad de la otra ). En ese caso, el area sería 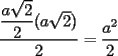 . .Caso 2) La altura es maxima, siendo igual al lado del cuadrado, entonces, la base sera el otro lado del cuadrado. Entonces el area de dicho triangulo será 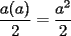 En ambos casos el area da 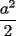 , demostrando que es la maxima area. WEEH..! , demostrando que es la maxima area. WEEH..!
Mensaje modificado por pelao_malo el Aug 5 2007, 09:14 PM
Archivo(s) Adjunto(s)
--------------------  |
|
|
|
 Aug 8 2007, 06:26 PM Aug 8 2007, 06:26 PM
Publicado:
#3
|
|
|
Dios Matemático Supremo Grupo: Usuario FMAT Mensajes: 878 Registrado: 14-May 07 Desde: Talcahuano Miembro Nº: 5.845 Nacionalidad:  Colegio/Liceo:  Sexo:  |
P1-
Sergio tomo 0.5 lt de te y los hecho al agua. Dejo el vaso de te con 1,5 lt de te. Dejo el vaso de agua con 2 lt de agua y 0.5 de te Como revolvio y dejo una mezcla, entonces podremos calcular la cantidad de agua y te que tienen los 50 cm de la mezcla extraida de la siguiente manera: En el vaso de agua hay 0.5 lt de agua+0.5 lt de agua+0.5 lt de agua+ 0.5 lt de agua+0.5 lt de te Como esta mezclado toma la misma parte de cada 1, osea : 0.1 lt de agua+0.1 lt de agua+0.1 lt de agua+0.1 lt de agua+0.1 lt de te osea, el vaso de agua queda con 1,6 lt de agua y 0.4 lt de te. Cuando vertimos los 50 cm de mezcla en el te, quedan 1,6 lt de te y 0.4 lt de agua en este. Concluyendo que el agua tiene igual té que el té tiene de agua. --------------------  |
|
|
|
 Aug 15 2007, 11:43 AM Aug 15 2007, 11:43 AM
Publicado:
#4
|
|
 Dios Matemático Supremo Grupo: Administrador Mensajes: 2.706 Registrado: 13-May 05 Desde: Santiago de Chile Miembro Nº: 10 Nacionalidad:  Colegio/Liceo:  Sexo:  |
P2= Bueno existen 2 casos para que el area del triangulo Dentro de un cuadrado de lado  sea la máxima: sea la máxima:Caso 1) La base es igual a la diagonal, que para que tenga area maxima, la altura debe ser igual a la la mitad de la otra diagonal ( que en el fondo mide lo mismo que la mitad de la otra ). En ese caso, el area sería 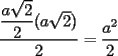 . .Caso 2) La altura es maxima, siendo igual al lado del cuadrado, entonces, la base sera el otro lado del cuadrado. Entonces el area de dicho triangulo será 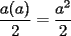 En ambos casos el area da 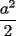 , demostrando que es la maxima area. WEEH..! , demostrando que es la maxima area. WEEH..!Tu solución es válida, siempre y cuando uno de los lados del triángulo coincida con uno de los lados o diagonales del cuadrado. Sin embargo, existen otros casos, que no has cubierto en tu explicación (que ninguno de los tres lados del triángulo, sean lados o diagonales del cuadrado) A completar la solución, entonces... -------------------- |
|
|
|
 Aug 15 2007, 11:46 AM Aug 15 2007, 11:46 AM
Publicado:
#5
|
|
 Dios Matemático Supremo Grupo: Administrador Mensajes: 2.706 Registrado: 13-May 05 Desde: Santiago de Chile Miembro Nº: 10 Nacionalidad:  Colegio/Liceo:  Sexo:  |
P1- Sergio tomo 0.5 lt de te y los hecho al agua. Dejo el vaso de te con 1,5 lt de te. Dejo el vaso de agua con 2 lt de agua y 0.5 de te Como revolvio y dejo una mezcla, entonces podremos calcular la cantidad de agua y te que tienen los 50 cm de la mezcla extraida de la siguiente manera: En el vaso de agua hay 0.5 lt de agua+0.5 lt de agua+0.5 lt de agua+ 0.5 lt de agua+0.5 lt de te Como esta mezclado toma la misma parte de cada 1, osea : 0.1 lt de agua+0.1 lt de agua+0.1 lt de agua+0.1 lt de agua+0.1 lt de te osea, el vaso de agua queda con 1,6 lt de agua y 0.4 lt de te. Cuando vertimos los 50 cm de mezcla en el te, quedan 1,6 lt de te y 0.4 lt de agua en este. Concluyendo que el agua tiene igual té que el té tiene de agua. En esta solución, asumiste que 50 cc = 0,5 lts, lo que está errado (50 cc = 0,05 lts). Esto complica un poco más la manera de expresar tu solución. Por cierto, la idea no está mal, y ya fue preguntado en el sector principiante (problemas de ingenio). Todavía esperamos la solución ingeniosa -------------------- |
|
|
|
 May 21 2010, 10:24 PM May 21 2010, 10:24 PM
Publicado:
#6
|
|
 Dios Matemático Supremo Grupo: Team Ensayos FMAT Mensajes: 1.559 Registrado: 18-November 07 Miembro Nº: 12.754 Nacionalidad:  Sexo:  |
Problema 5: El número 3 tiene las siguientes representaciones como suma de números positivos: 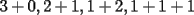 , considerando importante el orden en que se suma,excepto en el caso del 3. Mostrar que cualquier número entero positivo $n$ se puede expresar de , considerando importante el orden en que se suma,excepto en el caso del 3. Mostrar que cualquier número entero positivo $n$ se puede expresar de 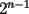 formas distintas con estas consideraciones de orden. formas distintas con estas consideraciones de orden.Veamos para los valores más pequeños de n.. 1=1 2=1+1=2 3= 1+1+1 = 1+2 = 2+1 = 3 4=1+1+1+1= 2+(1+2) = (1+2)+1 = 1+(2+1)=(2+1)+2= 3+1 = 1+3 etc... Bueno, luego de cierta observacion y análisis, ayudando al lector con las agrupaciones que realicé con paréntesis para que entienda mejor mis ideas, para n=1,2,3,4,5 , decidi que procedería inductivamente. Para n=1, vemos que 1 sólo se expresa como la suma siguiente: 1, es decir, hay solo 1 manera de expresarlo, que equivale a 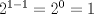 Luego, digamos inductivamente que esta proposición se cumple para un natural n. Ahora, buscaremos la manera de demostrar que si se cumple para n, se cumplirá para (n+1) Vemos que n se puede expresar de 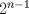 sumas distintas de enteros positivos. sumas distintas de enteros positivos. Observándolas, y comparándolas con las de (n+1), veremos luego que n+1 se puede expresar de las siguientes maneras: n+1. 1+1+...+1 (donde estos son (n+1) 1s) , y las restantes corresponden a 1+k, o k+1 donde k es una de las representaciones de n, excepto la de la forma 1+1+...+1 (con n 1s) Generalizando, vemos que n+1 se puede expresar de 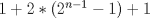 maneras, esto se basa en lo siguiente: el primer 1 corresponde la la representación (n+1), el segundo sumando corresponde a las permutaciones de la forma 1+k y k+1, con k representaciones de n, excepto las de forma 1+1+...+1 con n 1s, y el ultimo sumando corresponde a la representación 1+1+...+1 con (n+1) unos. maneras, esto se basa en lo siguiente: el primer 1 corresponde la la representación (n+1), el segundo sumando corresponde a las permutaciones de la forma 1+k y k+1, con k representaciones de n, excepto las de forma 1+1+...+1 con n 1s, y el ultimo sumando corresponde a la representación 1+1+...+1 con (n+1) unos.Esta ultima expresión puede desarrollarse de la siguiente manera: 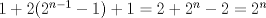 Luego, queda demostrado inductivamente que todo entero positivo n puede representarse de 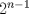 maneras distintas como suma de enteros positivos considerando el orden de estos sumandos. maneras distintas como suma de enteros positivos considerando el orden de estos sumandos.Saludos!! -------------------- Empezando con Desigualdades? Encuentra aquí problemas resueltos
|
|
|
|
 Jul 9 2010, 09:30 PM Jul 9 2010, 09:30 PM
Publicado:
#7
|
|
 Dios Matemático Supremo Grupo: Usuario FMAT Mensajes: 688 Registrado: 8-November 09 Desde: Villarrica Miembro Nº: 61.657 Nacionalidad:  Colegio/Liceo:  Universidad: .png) Sexo:  |

Mensaje modificado por Pedantic Anarchy el Jul 9 2010, 10:50 PM -------------------- yo no soy especial
a pesar que ella lo dijo tengo unos krk y un celular hechizo aún vácilo SFDK en el segundo piso y la frase final da igual la improviso |
|
|
|
 Jul 9 2010, 09:35 PM Jul 9 2010, 09:35 PM
Publicado:
#8
|
|
 Dios Matemático Supremo Grupo: Usuario FMAT Mensajes: 688 Registrado: 8-November 09 Desde: Villarrica Miembro Nº: 61.657 Nacionalidad:  Colegio/Liceo:  Universidad: .png) Sexo:  |
El problema 2 me causo un Deja vu
-------------------- yo no soy especial
a pesar que ella lo dijo tengo unos krk y un celular hechizo aún vácilo SFDK en el segundo piso y la frase final da igual la improviso |
|
|
|
 Jul 9 2010, 09:56 PM Jul 9 2010, 09:56 PM
Publicado:
#9
|
|
|
Dios Matemático Supremo Grupo: Usuario FMAT Mensajes: 2.818 Registrado: 3-October 09 Miembro Nº: 59.773 Nacionalidad:  Colegio/Liceo:  Universidad:  Sexo:  |
Super off topic... siempre que me pongo a leer las soluciones, quedo loco @.@
-------------------- Me voy, me jui.
|
|
|
|
 Jul 9 2010, 09:56 PM Jul 9 2010, 09:56 PM
Publicado:
#10
|
|
 Dios Matemático Supremo Grupo: Team Ensayos FMAT Mensajes: 1.559 Registrado: 18-November 07 Miembro Nº: 12.754 Nacionalidad:  Sexo:  |
Tomemos 3 puntos al interior del cuadrado ABCD de lado a, P,Q,R.
Luego, es fácil ver que el área del triángulo se maximizará cunado tenga máxma base y altura, por lo que P y Q deben coincidir con 2 vértices del cuadrado, y R estar en el lado opuesto a estos. Finalmente, este triángulo tendrá área correspondiente a la mitad del área del cuadrado. Luego, queda demostrado que no pueden tomarse 3 puntos al interior de un cuadrado tal que formen un triángulo de área mayor a la mitad del área del cuadrado. (Más formalmente hay un método con desigualdades que demuestra los lugares de P,Q y R tales que el área del triángulo mencionado se maximice, queda a cargo del lector, ya que es bastante intuitivo) Saludos! -------------------- Empezando con Desigualdades? Encuentra aquí problemas resueltos
|
|
|
|
  |
1 usuario(s) está(n) leyendo esta discusión (1 invitado(s) y 0 usuario(s) anónimo(s))
0 miembro(s):
| Versión Lo-Fi | Fecha y Hora actual: 2nd April 2025 - 02:38 AM |













