|
|
|
|
|
|
|
  |
 Feb 25 2007, 08:21 PM Feb 25 2007, 08:21 PM
Publicado:
#1
|
|
 Dios Matemático Supremo Grupo: Usuario FMAT Mensajes: 558 Registrado: 14-May 05 Desde: Maipú, Stgo, Chile Miembro Nº: 27 Nacionalidad:  Colegio/Liceo:  Universidad:  Sexo:  |
9ª OLIMPIADA NACIONAL DE MATEMÁTICAS Prueba de Clasificación Primera Prueba Problema 1: Se realiza una votación entre tres candidatos: 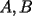 y y 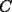 , con un electorado de 20 personas. Cada elector vota en orden por los tres candidatos, cada combinación posible recibe al menos un voto. De los electores, 11 prefieren a , con un electorado de 20 personas. Cada elector vota en orden por los tres candidatos, cada combinación posible recibe al menos un voto. De los electores, 11 prefieren a 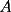 sobre sobre 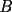 y 12 prefieren a y 12 prefieren a 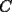 sobre sobre 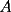 . Ante esto, la comisión electoral solicita a . Ante esto, la comisión electoral solicita a 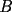 que se retire para realizar una elección sólo entre que se retire para realizar una elección sólo entre 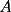 y y 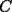 . Frente a esta petición, el candidato . Frente a esta petición, el candidato 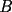 protesta y argumenta que hay 14 electores que lo prefieren sobre protesta y argumenta que hay 14 electores que lo prefieren sobre 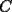 . Dada la confusión, la comisión electoral decide realizar una elección entre las dos primeras mayorías. Determine cuáles de los candidatos son los que obtuvieron las primeras mayorías, y cuántos votos obtuvieron. . Dada la confusión, la comisión electoral decide realizar una elección entre las dos primeras mayorías. Determine cuáles de los candidatos son los que obtuvieron las primeras mayorías, y cuántos votos obtuvieron.Problema 2: Para cada entero positivo  , pruebe que , pruebe que 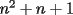 no es cuadrado perfecto. no es cuadrado perfecto.Problema 3: Encuentre todas las soluciones enteras de la ecuación: 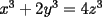 Segunda Prueba Problema 4: El 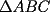 tiene circuncírculo tiene circuncírculo 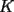 . Las bisectrices interiores del triángulo intersecan nuevamente a . Las bisectrices interiores del triángulo intersecan nuevamente a  en en 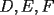 . El . El 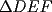 resulta ser equilátero. Pruebe que el resulta ser equilátero. Pruebe que el 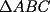 es equilátero. es equilátero.Problema 5: Sea 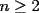 un natural. un natural. 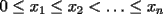 son reales, que suman 1. Si son reales, que suman 1. Si 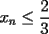 , pruebe que existe , pruebe que existe 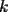 , con , con 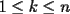 , tal que: , tal que: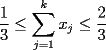 Problema 6: Sean 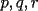 números enteros, donde números enteros, donde  no es cuadrado perfecto. Suponga que no es cuadrado perfecto. Suponga que![TEX: \begin{center}<br />$x=\sqrt[3]{p+\sqrt{r}}+\sqrt[3]{q-\sqrt{r}}$ <br />\end{center}](./tex/1172452929.gif) Es un racional. Pruebe que 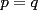 . .Problema 7: Considere una circunferencia  , de centro , de centro 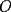 y radio y radio 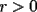 . Sea . Sea 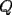 un punto en el interior de un punto en el interior de 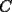 . Se localiza un punto . Se localiza un punto 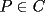 y se forma el y se forma el 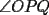 . ¿Dónde debe ubicarse el punto . ¿Dónde debe ubicarse el punto 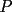 para que el para que el 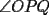 tenga medida máxima? tenga medida máxima?
-------------------- El peor defecto del ignorante es que ignora su propia ignorancia................
|
|
|
|
 Sep 3 2007, 07:58 PM Sep 3 2007, 07:58 PM
Publicado:
#2
|
|
|
Dios Matemático Supremo Grupo: Usuario FMAT Mensajes: 878 Registrado: 14-May 07 Desde: Talcahuano Miembro Nº: 5.845 Nacionalidad:  Colegio/Liceo:  Sexo:  |
P2.
Tenemos que asumir que 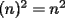 y el siguiente cuadrado perfecto más cercano es y el siguiente cuadrado perfecto más cercano es 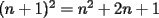 . Pero suponiendo que . Pero suponiendo que 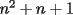 fuese un cuadrado perfecto, y teniendo en cuenta que fuese un cuadrado perfecto, y teniendo en cuenta que 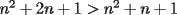 , tenemos que , tenemos que 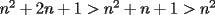 ,ya que ambos son positivos. Entonces ,ya que ambos son positivos. Entonces 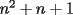 sería el cuadrado perfecto más cercano a sería el cuadrado perfecto más cercano a  , lo que contradice lo que hemos asumido. , lo que contradice lo que hemos asumido.
--------------------  |
|
|
|
 Sep 22 2007, 05:30 PM Sep 22 2007, 05:30 PM
Publicado:
#3
|
|
 Dios Matemático Supremo Grupo: Colaborador Gold Mensajes: 1.118 Registrado: 11-September 05 Desde: Valdivia/Ancud Miembro Nº: 302 Nacionalidad:  Colegio/Liceo:  Universidad:  Sexo:  |

-------------------- Comienza a crear documentos con LaTeX.
Ya usas LaTeX y quieres aprender un poco más ... pincha aquí Si eres de la UaCH ... únete a la causa !!! J. Jonathan H. Oberreuter A. Universidad Austral de Chile - RWTH Aachen alumni Est. Magister en Acústica y Vibraciones Ingeniero Civil Acústico (E) Bachiller y Licenciado en Cs. de la Ingeniería |
|
|
|
 Sep 22 2007, 05:37 PM Sep 22 2007, 05:37 PM
Publicado:
#4
|
|
 Dios Matemático Supremo Grupo: Colaborador Gold Mensajes: 1.118 Registrado: 11-September 05 Desde: Valdivia/Ancud Miembro Nº: 302 Nacionalidad:  Colegio/Liceo:  Universidad:  Sexo:  |

-------------------- Comienza a crear documentos con LaTeX.
Ya usas LaTeX y quieres aprender un poco más ... pincha aquí Si eres de la UaCH ... únete a la causa !!! J. Jonathan H. Oberreuter A. Universidad Austral de Chile - RWTH Aachen alumni Est. Magister en Acústica y Vibraciones Ingeniero Civil Acústico (E) Bachiller y Licenciado en Cs. de la Ingeniería |
|
|
|
 Sep 28 2007, 08:03 PM Sep 28 2007, 08:03 PM
Publicado:
#5
|
|
 Dios Matemático Supremo Grupo: Administrador Mensajes: 2.706 Registrado: 13-May 05 Desde: Santiago de Chile Miembro Nº: 10 Nacionalidad:  Colegio/Liceo:  Sexo:  |
La primera solución al P2 es correcta, básicamente por el acotamiento: n²<n²+n+1<(n+1)² (la segunda solución no la leí... estoy pasando rápido para evlauar las soluciones). La solución al problema 3 es correcta, aunque quiero discutir un poco más en detalle un punto... estamos demostrando que x, y, z tienen una cantidad infinita de factores 2 (es decir: 2^n|x, 2^n|y, 2^n|z, para todo n entero positivo). La única manera en que eso es posible, es cuando x=y=z=0
Sólo quería dar otro punto de vista sobre el mismo punto -------------------- |
|
|
|
 Apr 10 2010, 10:39 PM Apr 10 2010, 10:39 PM
Publicado:
#6
|
|
 Dios Matemático Supremo Grupo: Usuario FMAT Mensajes: 688 Registrado: 8-November 09 Desde: Villarrica Miembro Nº: 61.657 Nacionalidad:  Colegio/Liceo:  Universidad: .png) Sexo:  |
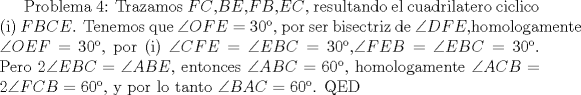
-------------------- yo no soy especial
a pesar que ella lo dijo tengo unos krk y un celular hechizo aún vácilo SFDK en el segundo piso y la frase final da igual la improviso |
|
|
|
 Dec 19 2010, 10:00 PM Dec 19 2010, 10:00 PM
Publicado:
#7
|
|
 Doctor en Matemáticas Grupo: Usuario FMAT Mensajes: 193 Registrado: 22-March 07 Desde: San Miguel, Santiago Miembro Nº: 4.651 Nacionalidad:  Colegio/Liceo:  Universidad:  Sexo:  |
 alguna justificacion de lo ultimo? (por directo que sea), propongo otra solucion. Consideremos que si es un cuadrado, es decir 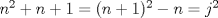 , luego , luego 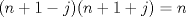 , lo cual es contradictorio pues , lo cual es contradictorio pues 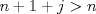 y por tanto no puede dividirlo. y por tanto no puede dividirlo.-------------------- |
|
|
|
 May 3 2011, 07:58 PM May 3 2011, 07:58 PM
Publicado:
#8
|
|
 Dios Matemático Grupo: Usuario FMAT Mensajes: 270 Registrado: 31-May 10 Desde: San antonio Miembro Nº: 71.730 Nacionalidad:  Colegio/Liceo:  Universidad:  Sexo:  |
P6 (no estoy muy seguro de la solución pero haber si la pueden corregir)
![TEX: $\sqrt[3]{p+\sqrt{r}}+\sqrt[3]{q-\sqrt{r}}=x$](./tex/49f08ae26c4702d4ff2e08e8aede278d.png) Hagamos un cambio de variable sea 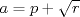 y y 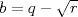 ![TEX: $\Rightarrow \sqrt[3]{a}+\sqrt[3]{b}=x$](./tex/9b01a4905b9304c5aa610d43cd5064dc.png) ![TEX: $\displaystyle \Rightarrow x=\sqrt[3]{a}+\sqrt[3]{b}\frac{\left( \sqrt[3]{a^{2}}-\sqrt[3]{ab}+\sqrt[3]{b^{2}} \right)}{\left( \sqrt[3]{a^{2}}-\sqrt[3]{ab}+\sqrt[3]{b^{2}} \right)}$](./tex/3fae7c12664a89b4850d1ccf65354bd7.png) ![TEX: $\displaystyle \Rightarrow x=\frac{a+b}{\left( \sqrt[3]{a^{2}}-\sqrt[3]{ab}+\sqrt[3]{b^{2}} \right)}$](./tex/e4e9404241a9c2b4ff0a52d5f46f253f.png) ![TEX: $\displaystyle \Rightarrow \left( \sqrt[3]{ab^{2}}-\sqrt[3]{ab}+\sqrt[3]{ab^{2}} \right)=\frac{a+b}{x}$](./tex/7a63acd318481d3b9b5a7612ae3112dd.png) ![TEX: $\displaystyle \Rightarrow \frac{a+b}{x}=\left( \sqrt[3]{a^{2}}-\sqrt[3]{ab}+\sqrt[3]{b^{2}}+3\sqrt[3]{ab}-3\sqrt[3]{ab} \right)$](./tex/2f459220a6b2072acd7bd7180acc8481.png) pero ![TEX: $\sqrt[3]{a^{2}}+2\sqrt[3]{ab}+\sqrt[3]{b^{2}}=x^{2}$](./tex/e532dd186fb32499c693122b8548ac1e.png) reemplazando en la expresión (es importante notar que x es racional por condición de enunciado) reemplazando en la expresión (es importante notar que x es racional por condición de enunciado)![TEX: $\displaystyle \Rightarrow \frac{a+b}{x}=\left( x^{2}-3\sqrt[3]{ab} \right)$](./tex/15ad6efc0769c4fdebb58c5ef1ded720.png) ![TEX: $\displaystyle \Rightarrow x^{2}-\frac{a+b}{x}=3\sqrt[3]{ab}$](./tex/847b7f8426846d3da3e388b971e3d0a9.png) ![TEX: $\displaystyle \frac{x^{3}-a+b}{3x}=\sqrt[3]{ab}$](./tex/1b85134afb9e73fc17a88e094bd3b5e1.png) 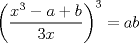 reemplazando por los valores de a y b se sigue que 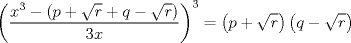 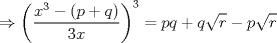 luego el lado izquierdo es racional y la única forma que el derecho lo sea es que p=q pues r no es un cuadrado perfecto Saludos |
|
|
|
 Jul 11 2011, 01:10 AM Jul 11 2011, 01:10 AM
Publicado:
#9
|
|
 Dios Matemático Supremo Grupo: Usuario FMAT Mensajes: 532 Registrado: 19-October 08 Desde: Santa Cruz de la Sierra Miembro Nº: 36.531 Nacionalidad:  Sexo:  |
Problema 5: Supongamos lo contrario. Sea
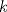 el menor entero posible tal que el menor entero posible tal que 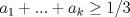 , si , si 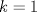 entonces entonces 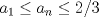 , contradiccion, osea , contradiccion, osea 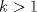 , luego tenemos que , luego tenemos que 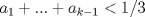 por la definicion de por la definicion de 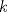 y que y que 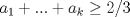 , luego de las dos ultimas desigualdades obtenemos , luego de las dos ultimas desigualdades obtenemos 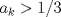 de donde de donde 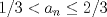 , osea , osea 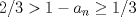 contradiccion. contradiccion.
-------------------- "I've never let my school interfere with my education.”
|
|
|
|
 Jul 16 2011, 12:10 AM Jul 16 2011, 12:10 AM
Publicado:
#10
|
|
|
Principiante Matemático Grupo: Usuario FMAT Mensajes: 1 Registrado: 15-July 11 Miembro Nº: 91.908 Nacionalidad:  Colegio/Liceo:  Universidad:  Sexo:  |
Buenas, mi primer aporte a esta comunidad. Yo fui seleccionado el año 1994, por ahí debo tener los problemas antiguos.
Preg 7. Se tienen dos puntos (O y Q), cuando buscamos el arco capaz, mientras mas pequeños sea el arco (de menor radio) el ángulo que forman es mayor. Entonces hay que buscar el menor arco que cruce la circunferencia C en al menos un punto. Este arco es el que es tangente a la circunferencia.  Saludos. |
|
|
|
  |
1 usuario(s) está(n) leyendo esta discusión (1 invitado(s) y 0 usuario(s) anónimo(s))
0 miembro(s):
| Versión Lo-Fi | Fecha y Hora actual: 2nd April 2025 - 02:26 AM |











