|
|
|
|
|
|
|
  |
 Mar 7 2011, 06:31 PM Mar 7 2011, 06:31 PM
Publicado:
#1
|
|
 Dios Matemático Supremo Grupo: Usuario FMAT Mensajes: 539 Registrado: 21-January 11 Desde: Santiago - Osorno - Chile Miembro Nº: 83.254 Nacionalidad:  Colegio/Liceo:  Universidad:  Sexo:  |
Hola cabros =D, nuevamente recurro a su vasto conocimiento de matemáticas para ayudar al necesitado jaujauajuajaua.
Resulta que llevo ya dos clases de mi nuevo ramo de cuarto medio electivo matemático que se llama "Procesos Infinitos", donde realmente vemos cálculo y ya empezamos con esto de los axiomas de cuerpo y órden, resulta que hoy empezamos con eso de demostrar los proposiciones, por ejemplo explicar por qué -(-x)=x etc... Resulta que tengo un serio problema al intentar demostrar dos teoremas, así que apelo a aquellos universitarios que me puedan ayudar para poder entenderlos, anda dando vueltas un documento por ahí sobre el tema pero las demostraciones son muy poco detalladas como para que un principiante entienda fácilmente. Estos son las proposiciones que me complican demostrar: 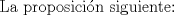 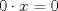 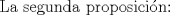 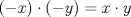 Su ayuda puede ser un hint, o tal vez la explicación detallada de estas proposiciones para entenderlas fácilmente, dado que las demás no me han complicado mucho excepto estas u.u Cualquier ayuda es bienvenida =)! de antemano gracias! =P PD: Si alguien tiene un material bastante ilustrativo y ojalá diferente a este: http://d.scribd.com/docs/1gzqkjiq2izr9tv404wb.pdf, si lo pusiera sería de una ayuda tremenda -------------------- Esteban A. Rodríguez M.
Ex- alumno Generación 2011 Colegio San Mateo-Osorno    "Por muy larga que sea la tormenta, el sol siempre vuelve a brillar entre las nubes" - Khalil Gibran |
|
|
|
 Mar 7 2011, 06:42 PM Mar 7 2011, 06:42 PM
Publicado:
#2
|
|
|
Dios Matemático Supremo Grupo: Usuario FMAT Mensajes: 1.255 Registrado: 22-February 08 Miembro Nº: 15.777 Sexo:  |
|
|
|
|
 Mar 7 2011, 06:44 PM Mar 7 2011, 06:44 PM
Publicado:
#3
|
|
 Dios Matemático Supremo Grupo: Usuario FMAT Mensajes: 539 Registrado: 21-January 11 Desde: Santiago - Osorno - Chile Miembro Nº: 83.254 Nacionalidad:  Colegio/Liceo:  Universidad:  Sexo:  |
ya vi el topic pero la guía que sale ahí explicando es la misma que sale en el link que puse, y realmente se salta muchos pasos para entender todo a la perfección u.u y no entiendo todo lo que hago para demostrar D: -------------------- Esteban A. Rodríguez M.
Ex- alumno Generación 2011 Colegio San Mateo-Osorno    "Por muy larga que sea la tormenta, el sol siempre vuelve a brillar entre las nubes" - Khalil Gibran |
|
|
|
 Mar 7 2011, 08:56 PM Mar 7 2011, 08:56 PM
Publicado:
#4
|
|
 Dios Matemático Supremo Grupo: Usuario FMAT Mensajes: 539 Registrado: 21-January 11 Desde: Santiago - Osorno - Chile Miembro Nº: 83.254 Nacionalidad:  Colegio/Liceo:  Universidad:  Sexo:  |
Nadie su humiRde cooperacion =D?
-------------------- Esteban A. Rodríguez M.
Ex- alumno Generación 2011 Colegio San Mateo-Osorno    "Por muy larga que sea la tormenta, el sol siempre vuelve a brillar entre las nubes" - Khalil Gibran |
|
|
|
 Mar 7 2011, 09:08 PM Mar 7 2011, 09:08 PM
Publicado:
#5
|
|
 Dios Matemático Supremo Grupo: Usuario FMAT Mensajes: 2.139 Registrado: 11-June 08 Desde: UK Miembro Nº: 26.837 Nacionalidad:  Colegio/Liceo:  Universidad:  Sexo:  |
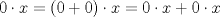 ahi se cancelan y listo. Los pasos en orden fueron la propiedad de elemento neutro, luego distributividad y al final cancelacion. ahi se cancelan y listo. Los pasos en orden fueron la propiedad de elemento neutro, luego distributividad y al final cancelacion.Para la segunda prueba que  es el inverso aditivo de es el inverso aditivo de 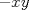 , como el inverso aditivo es unico estas listo , como el inverso aditivo es unico estas listo
-------------------- blep
|
|
|
|
 Mar 7 2011, 09:35 PM Mar 7 2011, 09:35 PM
Publicado:
#6
|
|
|
Dios Matemático Supremo Grupo: Usuario FMAT Mensajes: 2.818 Registrado: 3-October 09 Miembro Nº: 59.773 Nacionalidad:  Colegio/Liceo:  Universidad:  Sexo:  |
Hola E. Rodriguez, otra forma de ver propiedad de la multiplicación por cero es la siguiente.
Si 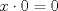 entonces debería cumplir la siguiente entonces debería cumplir la siguiente 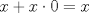 pues sería el neutro aditivo. Ahora, veamos si esto se cumple. pues sería el neutro aditivo. Ahora, veamos si esto se cumple. Que bueno que estén viendo eso en 4to medio. Saludos. -------------------- Me voy, me jui.
|
|
|
|
 Mar 7 2011, 09:56 PM Mar 7 2011, 09:56 PM
Publicado:
#7
|
|
|
Dios Matemático Supremo Grupo: Usuario FMAT Mensajes: 832 Registrado: 11-September 07 Desde: París, Francia Miembro Nº: 10.056 Nacionalidad:  Sexo:  |
Hola E. Rodriguez, otra forma de ver propiedad de la multiplicación por cero es la siguiente. Si 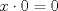 entonces debería cumplir la siguiente entonces debería cumplir la siguiente 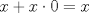 pues sería el neutro aditivo. Ahora, veamos si esto se cumple. pues sería el neutro aditivo. Ahora, veamos si esto se cumple. Que bueno que estén viendo eso en 4to medio. Saludos. parece que falta repasar logica... |
|
|
|
 Mar 7 2011, 10:02 PM Mar 7 2011, 10:02 PM
Publicado:
#8
|
|
|
Dios Matemático Supremo Grupo: Usuario FMAT Mensajes: 2.818 Registrado: 3-October 09 Miembro Nº: 59.773 Nacionalidad:  Colegio/Liceo:  Universidad:  Sexo:  |
¿Qué querías que le diera todo hecho? el amigo pidió un hint y yo le di uno nomás. Y cuando me refiero a "queda listo" es porque lo que falta es trivial.
Dios mio, eres totalmente desagradable para todos tus comentarios. Mensaje modificado por El Geek el Mar 7 2011, 10:04 PM -------------------- Me voy, me jui.
|
|
|
|
 Mar 7 2011, 10:06 PM Mar 7 2011, 10:06 PM
Publicado:
#9
|
|
 Doctor en Matemáticas Grupo: Usuario FMAT Mensajes: 160 Registrado: 27-May 09 Desde: Santiago Miembro Nº: 52.384 Nacionalidad:  Universidad:  Sexo:  |
La demostracion es al reves...
|
|
|
|
| ajenjo |
 Mar 7 2011, 10:12 PM Mar 7 2011, 10:12 PM
Publicado:
#10
|
|
Invitado |
Un clásico de la primera semana en la U xD, si te interesa resolver más ejercicios visita la pagina de matemáticas->docencia en los sitios de universidades. En la página de la dim parece que hay, en la usm tienes para entretenerte mucho tiempo buscando. En google teclea docencia matemática, MAT 021 (en el caso de la usm).
Mensaje modificado por ajenjo el Mar 7 2011, 10:13 PM |
|
|
|
  |
1 usuario(s) está(n) leyendo esta discusión (1 invitado(s) y 0 usuario(s) anónimo(s))
0 miembro(s):
| Versión Lo-Fi | Fecha y Hora actual: 4th April 2025 - 02:54 PM |









