Sumatoria con constante

Reglamento Sector de Consultas

Para un correcto uso de este foro debes leer estas reglas:

Este Sector es donde pueden plantear sus dudas de Nivel Universitario.
- NO se debe usar el Banco de Problemas Resueltos para consultar.
Se solicita a los usuarios el uso de LaTeX, para que llevemos una conversación al nivel que este sector requiere
Hacer UNA CONSULTA por TEMA, ya que asi es mas facil enfocarse solo a la pregunta.
- Si desean hacer varias preguntas, tendran que crear un tema para cada una.
- con un limite de 5 de un mismo tema por usuario, pues lo mas probable es que se resuelvan de forma similar
Respecto al TITULO, tratar de ser lo mas claro posible de que trata la consulta.
- Ejemplo de lo que no se debe hacer: "ayuda porfis" ó "Heeeeeelp!"
NO hacer doble posteo de una misma duda
- Buscar antes de preguntar (se recomienda usar el Motor de Busqueda).
El usuario que realiza la consulta debe manifestar si la respuesta dada por la Comunidad le fue o no satisfactoria.
NO doble postear, demuestre compromiso con su consulta.
Use el botón "Editar" si olvido algún detalle.
Si necesita ayuda urgente, exprese lo que ha intentado para resolver el problema
Usuario que no cumpla estas reglas, sera advertido (en el mismo post o via MP).
- En caso que incurra nuevamente a faltar al reglamento, sera amonestado.

Staff FMAT

Sumatoria con constante

Ditox Ver Perfil del Miembro Ver los mensajes de este miembro	Dec 26 2010, 04:48 PM Publicado: #1
Dios Matemático Supremo Grupo: Usuario FMAT Mensajes: 2.039 Registrado: 4-October 09 Desde: Valparaíso Miembro Nº: 59.794 Nacionalidad: Colegio/Liceo: Universidad: Sexo:	Una forma para resolver $TEX: \[\sum_{k=1}^{n}ka^k\]$ que es una suma (o el parecido a algunas) muy preguntada puede ser Sea $TEX: \[\sum_{k=1}^{n}ka^k=S\]$ $TEX: \[S=a+2a^2+3a^3+...(n-1)a^{n-1}+na^n\]$ $TEX: \[aS=a^2+2a^3+3a^4+...(n-1)a^{n}+na^{n+1}\]$ $TEX: \[S-aS=\underset{\sum_{k=1}^{n}a^k}{\underbrace{a+a^2+a^3+...a^{n-1}+a^n}}-na^{n+1}\]$ $TEX: \[aS-S=na^{n+1}-\sum_{k=1}^{n}a^k\]$ $TEX: \[S(a-1)=na^{n+1}-\left (\frac{a^{n+1}-a}{a-1} \right )\]$ $TEX: \[S(a-1)=\frac{na^{n+1}(a-1)+a-a^{n+1}}{a-1}\]$ $TEX: \[S=\frac{na^{n+1}(a-1)+a-a^{n+1}}{\left (a-1 \right )^2}\]$ Pueden poner otras formas Mensaje modificado por Ditox el Nov 9 2011, 08:49 PM --------------------

「Krizalid」 Ver Perfil del Miembro Ver los mensajes de este miembro	Dec 26 2010, 05:45 PM Publicado: #2
Staff FMAT Grupo: Super Moderador Mensajes: 8.124 Registrado: 21-May 06 Miembro Nº: 1.156 Nacionalidad: Sexo:	Sí, está bien, esa es la manera de proceder clásica. Hay otras formas, derivando, integrando, formando sumas telescópicas y la que se me ocurre ahora, usando sumas dobles. Se escribe 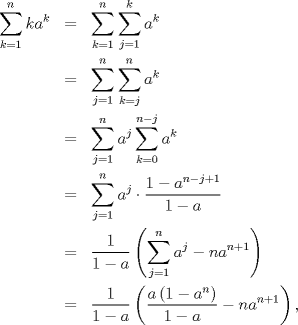$TEX: \begin{eqnarray}<br /> \sum\limits_{k=1}^{n}{k{{a}^{k}}}&=&\sum\limits_{k=1}^{n}{\sum\limits_{j=1}^{k}{{{a}^{k}}}} \\ <br /> & =&\sum\limits_{j=1}^{n}{\sum\limits_{k=j}^{n}{{{a}^{k}}}} \\ <br /> & =&\sum\limits_{j=1}^{n}{{{a}^{j}}\sum\limits_{k=0}^{n-j}{{{a}^{k}}}} \\ <br /> & =&\sum\limits_{j=1}^{n}{{{a}^{j}}\cdot \frac{1-{{a}^{n-j+1}}}{1-a}} \\ <br /> & =&\frac{1}{1-a}\left( \sum\limits_{j=1}^{n}{{{a}^{j}}}-n{{a}^{n+1}} \right) \\ <br /> & =&\frac{1}{1-a}\left( \frac{a\left( 1-{{a}^{n}} \right)}{1-a}-n{{a}^{n+1}} \right), <br />\end{eqnarray}<br />$ que es lo mismo que obtuviste.

Ditox Ver Perfil del Miembro Ver los mensajes de este miembro	Dec 26 2010, 06:28 PM Publicado: #3
Dios Matemático Supremo Grupo: Usuario FMAT Mensajes: 2.039 Registrado: 4-October 09 Desde: Valparaíso Miembro Nº: 59.794 Nacionalidad: Colegio/Liceo: Universidad: Sexo:	CITA(Krizalid @ Dec 26 2010, 06:45 PM) Sí, está bien, esa es la manera de proceder clásica. Hay otras formas, derivando, integrando, formando sumas telescópicas y la que se me ocurre ahora, usando sumas dobles. Se escribe 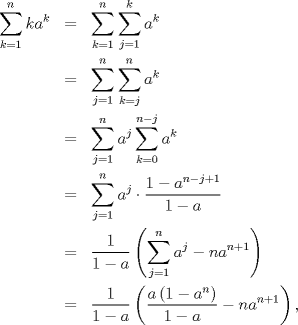$TEX: \begin{eqnarray}<br /> \sum\limits_{k=1}^{n}{k{{a}^{k}}}&=&\sum\limits_{k=1}^{n}{\sum\limits_{j=1}^{k}{{{a}^{k}}}} \\ <br /> & =&\sum\limits_{j=1}^{n}{\sum\limits_{k=j}^{n}{{{a}^{k}}}} \\ <br /> & =&\sum\limits_{j=1}^{n}{{{a}^{j}}\sum\limits_{k=0}^{n-j}{{{a}^{k}}}} \\ <br /> & =&\sum\limits_{j=1}^{n}{{{a}^{j}}\cdot \frac{1-{{a}^{n-j+1}}}{1-a}} \\ <br /> & =&\frac{1}{1-a}\left( \sum\limits_{j=1}^{n}{{{a}^{j}}}-n{{a}^{n+1}} \right) \\ <br /> & =&\frac{1}{1-a}\left( \frac{a\left( 1-{{a}^{n}} \right)}{1-a}-n{{a}^{n+1}} \right), <br />\end{eqnarray}<br />$ que es lo mismo que obtuviste. muchas gracias, vere aquello de las sumas dobles, veo que pueden simplificar bastante la vida --------------------

~Fatal_Collapse~ Ver Perfil del Miembro Ver los mensajes de este miembro	Dec 26 2010, 06:41 PM Publicado: #4
Dios Matemático Supremo Grupo: Usuario FMAT Mensajes: 1.564 Registrado: 12-November 07 Desde: La Union, XIV Region de los Rios Miembro Nº: 12.607 Nacionalidad: Colegio/Liceo: Universidad: Sexo:	En este hay otra forma simpática de proceder -------------------- Ricardo Vargas Obando Ex-alumno Deutsche Schule La Unión (Generación 2010, de los 150 años). Novato de Licenciatura en Matemática/Estadística, en la Pontificia Universidad Católica de Chile. Grupo de facebook de Novatos Matemática y Estadística PUC 2011 Currículum Olímpico: Medalla de Plata, XIX Olimpiada Nacional de Matemática Nivel Menor (2007) Medalla de Oro, XXI Olimpiada Nacional de Matemática Nivel Mayor (2009) Medalla de Bronce, XXV Olimpiada Iberoamericana de Matemática (2010) Medalla de Oro, XXII Olimpiada Nacional de Matemática Nivel Mayor (2010) "What we learned as children, that one plus one equals two, we know to be false. One plus one equals one. We even have a word when you plus another, equals one. That word is love." "Todos piensan en cambiar el mundo, pero nadie piensa en cambiarse a sí mismo."

Kaissa Ver Perfil del Miembro Ver los mensajes de este miembro	Dec 26 2010, 07:40 PM Publicado: #5
Dios Matemático Supremo Grupo: Usuario FMAT Mensajes: 9.897 Registrado: 6-April 08 Miembro Nº: 19.238 Nacionalidad: Colegio/Liceo: Sexo:	conozco otra forma jugando con telescopicas. PD: ahora que me acuerdo, y gracias al link de fatal... una pequeñisima diferencia de nivel entre la prueba de seleccion IMO chilena y las europeas xdddd -------------------- Este es un extracto de Qué es fmat by Kenshin. La pregunta para ti estimado(a) lector(a) es... ¿Qué haces tu para que ésto se cumpla?

febomon Ver Perfil del Miembro Ver los mensajes de este miembro	Jan 2 2011, 02:24 PM Publicado: #6
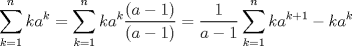Dios Matemático Grupo: Usuario FMAT Mensajes: 448 Registrado: 27-January 08 Miembro Nº: 15.045 Nacionalidad: Sexo:	El caso interesante es a distinto de 1 $TEX: <br />% MathType!MTEF!2!1!+-<br />% feaagaart1ev2aaatCvAUfeBSjuyZL2yd9gzLbvyNv2CaerbuLwBLn<br />% hiov2DGi1BTfMBaeXatLxBI9gBaerbd9wDYLwzYbItLDharqqtubsr<br />% 4rNCHbGeaGqiVu0Je9sqqrpepC0xbbL8F4rqqrFfpeea0xe9Lq-Jc9<br />% vqaqpepm0xbba9pwe9Q8fsY-rqaqpepae9pg0FirpepeKkFr0xfr-x<br />% fr-xb9adbaqaaeGaciGaaiaabeqaamaabaabaaGcbaWaaabCaeaaca<br />% WGRbGaamyyamaaCaaaleqabaGaam4AaaaaaeaacaWGRbGaeyypa0Ja<br />% aGymaaqaaiaad6gaa0GaeyyeIuoakiabg2da9maaqahabaGaam4Aai<br />% aadggadaahaaWcbeqaaiaadUgaaaaabaGaam4Aaiabg2da9iaaigda<br />% aeaacaWGUbaaniabggHiLdGcdaWcaaqaaiaacIcacaWGHbGaeyOeI0<br />% IaaGymaiaacMcaaeaacaGGOaGaamyyaiabgkHiTiaaigdacaGGPaaa<br />% aiabg2da9maalaaabaGaaGymaaqaaiaadggacqGHsislcaaIXaaaam<br />% aaqahabaGaam4AaiaadggadaahaaWcbeqaaiaadUgacqGHRaWkcaaI<br />% XaaaaOGaeyOeI0Iaam4AaiaadggadaahaaWcbeqaaiaadUgaaaaaba<br />% Gaam4Aaiabg2da9iaaigdaaeaacaWGUbaaniabggHiLdaaaa!62C3!<br />$$<br />\sum\limits_{k = 1}^n {ka^k } = \sum\limits_{k = 1}^n {ka^k } \frac{{(a - 1)}}<br />{{(a - 1)}} = \frac{1}<br />{{a - 1}}\sum\limits_{k = 1}^n {ka^{k + 1} - ka^k } <br />$$<br />$ $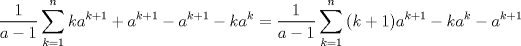TEX: <br />% MathType!MTEF!2!1!+-<br />% feaagaart1ev2aaatCvAUfeBSjuyZL2yd9gzLbvyNv2CaerbuLwBLn<br />% hiov2DGi1BTfMBaeXatLxBI9gBaerbd9wDYLwzYbItLDharqqtubsr<br />% 4rNCHbGeaGqiVu0Je9sqqrpepC0xbbL8F4rqqrFfpeea0xe9Lq-Jc9<br />% vqaqpepm0xbba9pwe9Q8fsY-rqaqpepae9pg0FirpepeKkFr0xfr-x<br />% fr-xb9adbaqaaeGaciGaaiaabeqaamaabaabaaGcbaWaaSaaaeaaca<br />% aIXaaabaGaamyyaiabgkHiTiaaigdaaaWaaabCaeaacaWGRbGaamyy<br />% amaaCaaaleqabaGaam4AaiabgUcaRiaaigdaaaGccqGHRaWkcaWGHb<br />% WaaWbaaSqabeaacaWGRbGaey4kaSIaaGymaaaakiabgkHiTiaadgga<br />% daahaaWcbeqaaiaadUgacqGHRaWkcaaIXaaaaOGaeyOeI0Iaam4Aai<br />% aadggadaahaaWcbeqaaiaadUgaaaaabaGaam4Aaiabg2da9iaaigda<br />% aeaacaWGUbaaniabggHiLdGccqGH9aqpdaWcaaqaaiaaigdaaeaaca<br />% WGHbGaeyOeI0IaaGymaaaadaaeWbqaaiaacIcacaWGRbGaey4kaSIa<br />% aGymaiaacMcacaWGHbWaaWbaaSqabeaacaWGRbGaey4kaSIaaGymaa<br />% aakiabgkHiTiaadUgacaWGHbWaaWbaaSqabeaacaWGRbaaaOGaeyOe<br />% I0IaamyyamaaCaaaleqabaGaam4AaiabgUcaRiaaigdaaaaabaGaam<br />% 4Aaiabg2da9iaaigdaaeaacaWGUbaaniabggHiLdaaaa!6A97!<br />$$<br />\frac{1}<br />{{a - 1}}\sum\limits_{k = 1}^n {ka^{k + 1} + a^{k + 1} - a^{k + 1} - ka^k } = \frac{1}<br />{{a - 1}}\sum\limits_{k = 1}^n {(k + 1)a^{k + 1} - ka^k - a^{k + 1} } <br />$$<br />$ de donde: $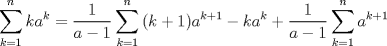TEX: <br />% MathType!MTEF!2!1!+-<br />% feaagaart1ev2aaatCvAUfeBSjuyZL2yd9gzLbvyNv2CaerbuLwBLn<br />% hiov2DGi1BTfMBaeXatLxBI9gBaerbd9wDYLwzYbItLDharqqtubsr<br />% 4rNCHbGeaGqiVu0Je9sqqrpepC0xbbL8F4rqqrFfpeea0xe9Lq-Jc9<br />% vqaqpepm0xbba9pwe9Q8fsY-rqaqpepae9pg0FirpepeKkFr0xfr-x<br />% fr-xb9adbaqaaeGaciGaaiaabeqaamaabaabaaGcbaWaaabCaeaaca<br />% WGRbGaamyyamaaCaaaleqabaGaam4AaaaaaeaacaWGRbGaeyypa0Ja<br />% aGymaaqaaiaad6gaa0GaeyyeIuoakiabg2da9maalaaabaGaaGymaa<br />% qaaiaadggacqGHsislcaaIXaaaamaaqahabaGaaiikaiaadUgacqGH<br />% RaWkcaaIXaGaaiykaiaadggadaahaaWcbeqaaiaadUgacqGHRaWkca<br />% aIXaaaaOGaeyOeI0Iaam4AaiaadggadaahaaWcbeqaaiaadUgaaaaa<br />% baGaam4Aaiabg2da9iaaigdaaeaacaWGUbaaniabggHiLdGccqGHRa<br />% WkdaWcaaqaaiaaigdaaeaacaWGHbGaeyOeI0IaaGymaaaadaaeWbqa<br />% aiaadggadaahaaWcbeqaaiaadUgacqGHRaWkcaaIXaaaaaqaaiaadU<br />% gacqGH9aqpcaaIXaaabaGaamOBaaqdcqGHris5aaaa!61BD!<br />$$<br />\sum\limits_{k = 1}^n {ka^k } = \frac{1}<br />{{a - 1}}\sum\limits_{k = 1}^n {(k + 1)a^{k + 1} - ka^k } + \frac{1}<br />{{a - 1}}\sum\limits_{k = 1}^n {a^{k + 1} } <br />$$<br />$ Saludos la primera es una telescopica y la segunda es una geometrica Mensaje modificado por febomon el Jan 2 2011, 02:28 PM

Jordiel Ver Perfil del Miembro Ver los mensajes de este miembro	Mar 9 2011, 05:28 PM Publicado: #7
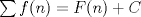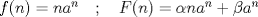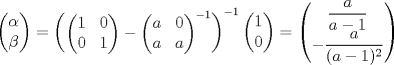Principiante Matemático Destacado Grupo: Usuario FMAT Mensajes: 22 Registrado: 17-May 10 Miembro Nº: 70.906 Nacionalidad: Sexo:	Si $TEX: $ \sum f(n)=F(n)+C$$ siendo $TEX: $f(n)=na^n\quad;\quad F(n)=\alpha na^n +\beta a^n$$ entonces $TEX: $\begin{pmatrix}\alpha \\ \beta \end{pmatrix}=\begin{pmatrix}{\begin{pmatrix}1&0\\ 0&1\end{pmatrix}}-{\begin{pmatrix}a&0\\ a&a\end{pmatrix}}^{-1}\end{pmatrix}^{-1}\begin{pmatrix}1\\ 0 \end{pmatrix}=\begin{pmatrix}\dfrac{a}{a-1}\\ -\dfrac{a}{(a-1)^2}\end{pmatrix}$$ $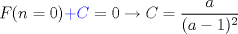TEX: $F(n=0){\color{blue}+C}=0\rightarrow C=\dfrac{a}{(a-1)^2}$$ $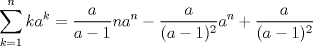TEX: $\displaystyle\sum_{k=1}^{n}ka^k=\dfrac{a}{a-1}na^n-\dfrac{a}{(a-1)^2}a^n+\dfrac{a}{(a-1)^2}$$ Editado: faltaba una constante. Mensaje modificado por Jordiel el Mar 12 2011, 07:09 PM

Ditox Ver Perfil del Miembro Ver los mensajes de este miembro	Nov 12 2011, 01:59 PM Publicado: #8
Dios Matemático Supremo Grupo: Usuario FMAT Mensajes: 2.039 Registrado: 4-October 09 Desde: Valparaíso Miembro Nº: 59.794 Nacionalidad: Colegio/Liceo: Universidad: Sexo:	Ahora que lo veo nuevamente, se pueden formas casos interesantes con argumentos tales como $TEX: \[k^2a^k,\; k^3a^k,...\]<br />$ --------------------

ironman18 Ver Perfil del Miembro Ver los mensajes de este miembro	Nov 12 2011, 09:38 PM Publicado: #9
Matemático Grupo: Usuario FMAT Mensajes: 42 Registrado: 31-October 11 Miembro Nº: 96.444 Nacionalidad: Colegio/Liceo: Universidad: Sexo:	CITA(Krizalid @ Dec 26 2010, 07:45 PM) Sí, está bien, esa es la manera de proceder clásica. Hay otras formas, derivando, integrando, formando sumas telescópicas y la que se me ocurre ahora, usando sumas dobles. Se escribe 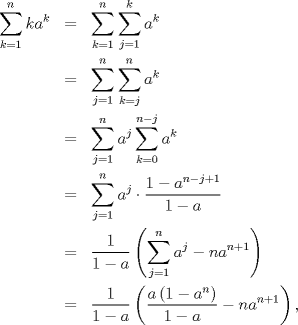$TEX: \begin{eqnarray}<br /> \sum\limits_{k=1}^{n}{k{{a}^{k}}}&=&\sum\limits_{k=1}^{n}{\sum\limits_{j=1}^{k}{{{a}^{k}}}} \\ <br /> & =&\sum\limits_{j=1}^{n}{\sum\limits_{k=j}^{n}{{{a}^{k}}}} \\ <br /> & =&\sum\limits_{j=1}^{n}{{{a}^{j}}\sum\limits_{k=0}^{n-j}{{{a}^{k}}}} \\ <br /> & =&\sum\limits_{j=1}^{n}{{{a}^{j}}\cdot \frac{1-{{a}^{n-j+1}}}{1-a}} \\ <br /> & =&\frac{1}{1-a}\left( \sum\limits_{j=1}^{n}{{{a}^{j}}}-n{{a}^{n+1}} \right) \\ <br /> & =&\frac{1}{1-a}\left( \frac{a\left( 1-{{a}^{n}} \right)}{1-a}-n{{a}^{n+1}} \right), <br />\end{eqnarray}<br />$ que es lo mismo que obtuviste. He buscado propiedades de las sumas dobles y aún así no puedo entender tu desarrollo, me complica que los extremos dependan de los subíndices ¿Podrías explicar los pasos para llegar hasta la tercera suma doble? Entiendo solamente la transformación de la suma inicial en una suma doble :B (o al menos decir q propiedad usaste)

「Krizalid」 Ver Perfil del Miembro Ver los mensajes de este miembro	Nov 13 2011, 07:40 AM Publicado: #10
Staff FMAT Grupo: Super Moderador Mensajes: 8.124 Registrado: 21-May 06 Miembro Nº: 1.156 Nacionalidad: Sexo:	Para cambiar el orden de la suma, leer: El resto es aplicación de suma geométrica.

« Posterior · Consultas de la Semana · Anterior »

1 usuario(s) está(n) leyendo esta discusión (1 invitado(s) y 0 usuario(s) anónimo(s))

0 miembro(s):