Control 3 2010/2 - Foro fmat.cl

Portal Matemático

¿Qué es FMAT?

Foro fmat.cl > Programa Enseñanza Universitaria > Comunidades Universitarias > Universidad de Chile > Cálculo Avanzado

Reply to this topic

Start new topic

Control 3 2010/2, Impropias, Serie/Transformada de Fourier

Crash! Ver Perfil del Miembro Ver los mensajes de este miembro	Dec 19 2010, 01:53 PM Publicado: #1
Dios Matemático Supremo Grupo: Usuario FMAT Mensajes: 929 Registrado: 22-June 08 Desde: Santiago Miembro Nº: 27.979 Nacionalidad: Colegio/Liceo: Universidad: Sexo:	$TEX: \[\begin{gathered}<br /> \left. {\underline {\, <br /> {{\text{P1}}} \,}}\! \right\| \hfill \\<br /> {\text{a) (3 puntos) Demuestre que para }}a > 0,\;b > 0{\text{ se tiene que:}} \hfill \\<br /> \int\limits_{ - \infty }^\infty {\frac{{\cos \left( {ax} \right) - \cos \left( {bx} \right)}}<br />{{{x^2}}}dx} = \pi \left( {b - a} \right) \hfill \\<br /> {\text{ Con lo anterior deduzca que}} \hfill \\<br /> \int\limits_{ - \infty }^\infty {{{\left( {\frac{{\sin \left( x \right)}}<br />{x}} \right)}^2}dx} = \pi \hfill \\<br /> {\text{Indicacion: Explicite sobre que contorno est\'a integrando y justifique la validez de los teoremas}} \hfill \\<br /> {\text{usados}}{\text{. Recuerde ademas que si consideramos el polinomio }}p\left( x \right) = {c_2}{x^2} + {c_1}x + {c_0},{\text{ entonces se}} \hfill \\<br /> {\text{tiene que su factorizacion es }}p\left( x \right) = {c_2}\left( {x - {x_1}} \right)\left( {x - {x_2}} \right),{\text{ donde }}{x_1}{\text{ y }}{x_2}{\text{ son las raices del polinomio}}{\text{.}} \hfill \\<br /> \hfill \\<br /> {\text{b) (3 puntos) Demuestre que}} \hfill \\<br /> \int\limits_0^{2\pi } {\frac{{dt}}<br />{{a + b\cos \left( t \right) + c\sin \left( t \right)}}} = \frac{{2\pi }}<br />{{\sqrt {{a^2} - {b^2} - {c^2}} }} \hfill \\<br /> {\text{para todo }}a,\;b,\;c \in \mathbb{R}{\text{ tales que }}{a^2} > {b^2} + {c^2}. \hfill \\ <br />\end{gathered} \]<br />$ $TEX: \[\begin{gathered}<br /> \left. {\underline {\, <br /> {{\text{P2}}} \,}}\! \right\| \hfill \\<br /> {\text{a) (4 puntos) Encuentre el desarrollo en serie de Fourier de la funcion}} \hfill \\<br /> f\left( x \right) = \cos \left( {\alpha x} \right),\; - \pi < x < \pi \hfill \\<br /> {\text{para cualquier }}\alpha {\text{ no entero}}{\text{.}} \hfill \\<br /> \hfill \\<br /> {\text{Concluya que}} \hfill \\<br /> \cot \left( {\alpha x} \right) = \frac{1}<br />{\pi }\left( {\frac{1}<br />{\alpha } - \sum\limits_{n = 1}^\infty {\frac{{2\alpha }}<br />{{{n^2} - {\alpha ^2}}}} } \right) \hfill \\<br /> {\text{si }}\alpha {\text{ no es entero}}{\text{. Explique}}{\text{.}} \hfill \\<br /> \hfill \\<br /> {\text{b) (2 puntos) Calcule la Transformada de Fourier de la funcion}} \hfill \\<br /> f\left( x \right) = \left\{ {\begin{array}{*{20}{c}}<br /> {\left( {x - 3} \right){e^{ - 4x}}\;{\text{si }}x \geqslant 3,} \\<br /> {\;\;\;\;0\;\;\;\;\;\;\;\;\;\;{\text{si }}x < 3.} \\<br /><br /> \end{array} } \right. \hfill \\ <br />\end{gathered} \]<br />$ $TEX: \[\begin{gathered}<br /> \left. {\underline {\, <br /> {{\text{P3}}} \,}}\! \right\| {\text{ Resuelva el problema:}} \hfill \\<br /> {u_t} - {u_{xx}} + 2tu = 0,\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;0 < x < \frac{1}<br />{2},\;t > 0 \hfill \\<br /> {u_x}\left( {0,t} \right) = u\left( {\frac{1}<br />{2},t} \right) = 0,\;\;\;\;\;\;\;\;\;t > 0 \hfill \\<br /> u\left( {x,0} \right) = 1 - 2x,\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;0 < x < \frac{1}<br />{2} \hfill \\<br /> \left. {\underline {\, <br /> {{\text{Tiempo: 3 horas}}{\text{.}}} \,}}\! \right\| \hfill \\ <br />\end{gathered} \]<br />$ Sorry la demora. Comentario personal: Fue lejos mi peor control, pésima idea presentarme a lo americo. -------------------- Ex-Electrico Usach 2008 Mechón Injenieria 2009 Tengo Sed.

Abu-Khalil Ver Perfil del Miembro Ver los mensajes de este miembro	Dec 19 2010, 08:33 PM Publicado: #2
Dios Matemático Supremo Grupo: Usuario FMAT Mensajes: 3.812 Registrado: 4-November 07 Desde: Santiago Miembro Nº: 12.213 Nacionalidad: Colegio/Liceo: Universidad: Sexo:	$TEX: \noindent Sean $R>\delta>0$. Consideremos $\gamma=\gamma_1\cup\gamma_2\cup\gamma_3\cup\gamma_4$, donde $\gamma_1$ como la recta que va desde $(-R,0)$ hasta $(-\delta,0)$, $\gamma_2$ como la semicircunferencia centrada en el origen de radio $\delta$, $\gamma_3$ la recta que va desde $(\delta,0)$ hasta $(R,0)$ y $\gamma_4$ como la semicircunferencia centrada en el origen y de radio $R$. Por supuesto, todo recorrido en el sentido habitual.\\<br />\\<br />Sea $f(z)=\dfrac{e^{iaz}-e^{ibz}}{z}$. Como $f$ es analítica al interior de $\gamma$, tenemos que<br />$$\int_{\gamma_1} f(z)dz+\int_{\gamma_2} f(z)dz+\int_{\gamma_3} f(z)dz+\int_{\gamma_4} f(z)dz=0.$$<br />Pero <br />$$\left\|\int_{\gamma_4}f(z)dz\right\|\le\int_{\gamma_4}\frac{\left\|e^{iaz}\right\|+\left\|e^{ibz}\right\|}{R^2}\|dz\|\le\frac 1{R^2}\int_{\gamma_4}\left(e^{-ay}+e^{-by}\right)\|dz\|\le\frac{2\pi}{R}\to 0,$$<br />cuando $R\uparrow\infty$ pues $b,a,y>0$.\\<br />\\<br />Por otro lado, usando el teorema de convergencia favorito de cada uno,<br />\begin{equation}\begin{aligned}<br />-\lim_{\delta\downarrow 0}\int_{\gamma_3}f(z)dz&=\lim_{\delta\downarrow 0}\int_0^\pi \frac{e^{ia\delta e^{i\theta}}-e^{ib\delta e^{i\theta}}}{\delta e^{i\theta}}id\theta=\int_0^\pi\lim_{\delta\downarrow 0} \frac{e^{ia\delta e^{i\theta}}-e^{ib\delta e^{i\theta}}}{\delta e^{i\theta}}id\theta\\<br />&\overset{\text{\tiny (L'H)}}=\int_0^\pi\lim_{\delta\downarrow 0} \frac{e^{ia\delta e^{i\theta}}iae^{i\theta}-e^{ib\delta e^{i\theta}}ibe^{i\theta}}{e^{i\theta}}id\theta=\int_0^\pi\lim_{\delta\downarrow 0}be^{ib\delta e^{i\theta}}-ae^{ia\delta e^{i\theta}}d\theta\\<br />&=(b-a)\int_0^\pi d\theta=\pi(b-a).<br />\end{aligned}\end{equation}<br />Finalmente, como $\Im f$ es impar sobre $\mathbb R$, tenemos que<br />$$\lim_{\substack{\delta\downarrow 0\\R\uparrow\infty}}\int_{\gamma_1}f(z)dz+\int_{\gamma_3}f(z)dz=\int_{-\infty}^{\infty}f(x)dx=\int_{-\infty}^{\infty}\frac{\cos(ax)-\cos(bx)}{x^2}dx.$$<br />Así, <br />$$\int_{-\infty}^{\infty}\frac{\cos(ax)-\cos(bx)}{x^2}dx=\pi(b-a).$$<br />Finalmente, tomando $b=1$ y $a=0$, obtenemos<br />$$\pi=\int_{-\infty}^{\infty}\frac{1-\cos x}{x^2}dx=2\int_{-\infty}^{\infty}\frac{\sin^2\frac x2}{x^2}dx=2\int_{-\infty}^{\infty}\frac{\sin^2 u}{(2u)^2}2du=\int_{-\infty}^{\infty}\left(\frac{\sin u}{u}\right)^2du.\quad\square$$<br />$ -------------------- ~milopez $TEX: \[\mathfrak{L}=\int_{-\infty}^\infty e^{-289x^2}dx=\frac{\Gamma (\frac{1}{2})}{17}=\frac{\sqrt{\pi}}{17}\]$ $TEX: <br />\begin{equation}\begin{aligned}<br />dS_t&=\mu S_t dt+\sqrt{V_t}S_t dW^S_t\\<br />dV_t&=\kappa(\theta-V_t)dt+\sigma\sqrt{V_t} dW^V_t\\<br />\end{aligned}\end{equation}<br />$ $TEX: <br />$$\mathbb A^{\text U}_M(N)$$<br />$

Naxoo Ver Perfil del Miembro Ver los mensajes de este miembro	Dec 20 2010, 05:00 PM Publicado: #3
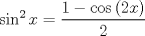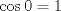Staff FMAT Grupo: Moderador Mensajes: 2.604 Registrado: 2-March 07 Desde: Somewhere over the rainbow Miembro Nº: 4.244 Nacionalidad: Colegio/Liceo: Universidad: Sexo:	o también usando $TEX: $\sin ^2 x=\dfrac{1-\cos \left(2x \right)}{2}$$ , como $TEX: $\cos 0=1$$ , tomando a=0 y b=2 estamos listos -------------------- INRIA - Francia, Sophia Antipolis Biocore Team Ingeniero Civil en Biotecnología Ingeniería Civil Químico “(…) los elementos que él (¿o Él?) [Dios] mismo nos ha dado (raciocinio, sensibilidad, intuición) no son en absoluto suficientes como para garantizarnos ni su existencia ni su no existencia. Gracias a una corazonada puedo creer en Dios y acertar o no creer en Dios y también acertar" Mario Benedetti $TEX: \[\iiint\limits_\Omega {\left( {\nabla \cdot \vec F} \right)dV} = \iint\limits_{\partial \Omega } {\left( {\vec F \cdot \hat n} \right)}dS\]<br />$

Crash! Ver Perfil del Miembro Ver los mensajes de este miembro	Dec 20 2010, 05:47 PM Publicado: #4
Dios Matemático Supremo Grupo: Usuario FMAT Mensajes: 929 Registrado: 22-June 08 Desde: Santiago Miembro Nº: 27.979 Nacionalidad: Colegio/Liceo: Universidad: Sexo:	Nacho, subete el C1 que yo no se subir los dibujos! xD -------------------- Ex-Electrico Usach 2008 Mechón Injenieria 2009 Tengo Sed.

Krebante Ver Perfil del Miembro Ver los mensajes de este miembro	Dec 20 2010, 06:55 PM Publicado: #5
Dios Matemático Supremo Grupo: Usuario FMAT Mensajes: 618 Registrado: 8-June 08 Desde: Paris Miembro Nº: 26.525 Nacionalidad: Colegio/Liceo: Universidad: Sexo:	Yo lo subo XD. -------------------- ¡Por más representación, vota Riesz!

Crash! Ver Perfil del Miembro Ver los mensajes de este miembro	Dec 20 2010, 08:44 PM Publicado: #6
Dios Matemático Supremo Grupo: Usuario FMAT Mensajes: 929 Registrado: 22-June 08 Desde: Santiago Miembro Nº: 27.979 Nacionalidad: Colegio/Liceo: Universidad: Sexo:	$TEX: \[\begin{gathered}<br /> \left. {\underline {\, <br /> {{\text{P1}}} \,}}\! \right\| {\text{ b)}} \hfill \\<br /> I = \int\limits_0^{2\pi } {\frac{{dt}}<br />{{a + b\cos \left( t \right) + c\sin \left( t \right)}}} \hfill \\<br /> I = \int\limits_0^{2\pi } {\frac{{dt}}<br />{{a + b\frac{{{e^{it}} + {e^{ - it}}}}<br />{2} + c\frac{{{e^{it}} - {e^{ - it}}}}<br />{{2i}}}}} \hfill \\<br /> I = \frac{1}<br />{i}\int\limits_0^{2\pi } {\frac{{i{e^{it}}dt}}<br />{{{e^{it}}\left( {a + b\frac{{{e^{it}} + {e^{ - it}}}}<br />{2} + c\frac{{{e^{it}} - {e^{ - it}}}}<br />{{2i}}} \right)}}} \hfill \\<br /> I = \frac{1}<br />{i}\oint\limits_{\left\| z \right\| = 1} {\frac{{dz}}<br />{{z\left( {a + b\frac{{z + {z^{ - 1}}}}<br />{2} + c\frac{{z - {z^{ - 1}}}}<br />{{2i}}} \right)}}} \hfill \\<br /> I = 2\oint\limits_{\left\| z \right\| = 1} {\frac{{dz}}<br />{{2aiz + bi\left( {{z^2} + 1} \right) + c\left( {{z^2} - 1} \right)}}} \hfill \\<br /> I = 2\oint\limits_{\left\| z \right\| = 1} {\frac{{dz}}<br />{{\left( {bi + c} \right){z^2} + 2aiz + \left( {bi - c} \right)}}} \hfill \\<br /> I = \frac{2}<br />{{bi + c}}\oint\limits_{\left\| z \right\| = 1} {\frac{{dz}}<br />{{\left( {z - {z_1}} \right)\left( {z - {z_2}} \right)}}} \hfill \\ <br />\end{gathered} \]<br />$ $TEX: \[\begin{gathered}<br /> {z_1} = - \frac{{\left( {a - \sqrt {{a^2} - {b^2} - {c^2}} } \right)\left( {b + ci} \right)}}<br />{{{b^2} + {c^2}}}\;;\;{z_2} = - \frac{{\left( {a + \sqrt {{a^2} - {b^2} - {c^2}} } \right)\left( {b + ci} \right)}}<br />{{{b^2} + {c^2}}} \hfill \\<br /> \left\| {{z_1}} \right\| = \frac{{a - \sqrt {{a^2} - {b^2} - {c^2}} }}<br />{{\sqrt {{b^2} + {c^2}} }} \cdot \frac{{a + \sqrt {{a^2} - {b^2} - {c^2}} }}<br />{{a + \sqrt {{a^2} - {b^2} - {c^2}} }} = \frac{{\sqrt {{b^2} + {c^2}} }}<br />{{\left( {a + \sqrt {{a^2} - {b^2} - {c^2}} } \right)}} < 1 \hfill \\<br /> \left\| {{z_2}} \right\| = \frac{{\left( {a + \sqrt {{a^2} - {b^2} - {c^2}} } \right)}}<br />{{\sqrt {{b^2} + {c^2}} }} > 1 \hfill \\<br /> \therefore I = \frac{2}<br />{{bi + c}}\oint\limits_{\left\| z \right\| = 1} {\frac{{dz}}<br />{{\left( {z - {z_1}} \right)\left( {z - {z_2}} \right)}}} = 2\pi i\frac{2}<br />{{bi + c}}\left( {\frac{1}<br />{{{z_1} - {z_2}}}} \right) \hfill \\<br /> {\text{y }}{z_1} - {z_2} = \frac{2}<br />{{\left( {b - ci} \right)}}\sqrt {{a^2} - {b^2} - {c^2}} \hfill \\<br /> \therefore I = \frac{{2\pi }}<br />{{\sqrt {{a^2} - {b^2} - {c^2}} }} \hfill \\ <br />\end{gathered} \]<br />$ Si, la pauta del dim está pifeada en este problema, en la justificacion de si la singularidad esta dentro del contorno o no Mensaje modificado por Crash! el Dec 20 2010, 08:46 PM -------------------- Ex-Electrico Usach 2008 Mechón Injenieria 2009 Tengo Sed.

Naxoo Ver Perfil del Miembro Ver los mensajes de este miembro	Dec 23 2010, 08:39 PM Publicado: #7
Staff FMAT Grupo: Moderador Mensajes: 2.604 Registrado: 2-March 07 Desde: Somewhere over the rainbow Miembro Nº: 4.244 Nacionalidad: Colegio/Liceo: Universidad: Sexo:	QUOTE(Crash! @ Dec 20 2010, 06:47 PM) Nacho, subete el C1 que yo no se subir los dibujos! xD Te me adelantaste en todos los controles xD, igual no le hago asco, es un lata tipiarlos. -------------------- INRIA - Francia, Sophia Antipolis Biocore Team Ingeniero Civil en Biotecnología Ingeniería Civil Químico “(…) los elementos que él (¿o Él?) [Dios] mismo nos ha dado (raciocinio, sensibilidad, intuición) no son en absoluto suficientes como para garantizarnos ni su existencia ni su no existencia. Gracias a una corazonada puedo creer en Dios y acertar o no creer en Dios y también acertar" Mario Benedetti $TEX: \[\iiint\limits_\Omega {\left( {\nabla \cdot \vec F} \right)dV} = \iint\limits_{\partial \Omega } {\left( {\vec F \cdot \hat n} \right)}dS\]<br />$

danielomalmsteen Ver Perfil del Miembro Ver los mensajes de este miembro	Dec 23 2010, 10:32 PM Publicado: #8
Dios Matemático Supremo Grupo: Usuario FMAT Mensajes: 3.413 Registrado: 13-March 08 Desde: Al frente del mundo Magico Miembro Nº: 16.846 Nacionalidad: Colegio/Liceo: Universidad: Sexo:	CITA(Naxoo @ Dec 23 2010, 09:39 PM) Te me adelantaste en todos los controles xD, igual no le hago asco, es un lata tipiarlos. Asi con los controles mal tipeados xD --------------------

Crash! Ver Perfil del Miembro Ver los mensajes de este miembro	Dec 23 2010, 11:34 PM Publicado: #9
Dios Matemático Supremo Grupo: Usuario FMAT Mensajes: 929 Registrado: 22-June 08 Desde: Santiago Miembro Nº: 27.979 Nacionalidad: Colegio/Liceo: Universidad: Sexo:	por cada respuesta minimo que se tiren una solucion po cabros xD -------------------- Ex-Electrico Usach 2008 Mechón Injenieria 2009 Tengo Sed.

« Posterior · Cálculo Avanzado · Anterior »

Reply to this topic

Start new topic

1 usuario(s) está(n) leyendo esta discusión (1 invitado(s) y 0 usuario(s) anónimo(s))

0 miembro(s):

Modo de Ver: Estándar · Cambiar a: Lineal+ · Cambiar a: Outline

Suscribirse · Enviar por correo · Imprimir · Suscribirse a este foro

Versión Lo-Fi

Fecha y Hora actual: 6th March 2025 - 10:27 PM

Powered By IP.Board 2.2.1 © 2007 IPS, Inc.