|
|
|
|
|
|
|
  |
 Jan 24 2007, 01:29 AM Jan 24 2007, 01:29 AM
Publicado:
#1
|
|
 Dios Matemático Supremo Grupo: Moderador Mensajes: 765 Registrado: 25-November 05 Desde: Algun lugar de la V region Miembro Nº: 415 Nacionalidad:  Colegio/Liceo:  Universidad:  Sexo:  |
INDUCCION MATEMATICA En la matemática se hace necesario, en muchas ocasiones, demostrar proposiciones, para esto existen métodos, uno de ellos llamado Inducción Matemática Por lo tanto el objetivo de esta guía es: Utilizar Inducción Matemática para demostrar proposiciones que involucren variables naturales. La Inducción es un razonamiento que permite demostrar una infinidad de proposiciones, o una proposición que depende de un parámetro "n"que toma una infinidad de valores, usualmente en el conjunto de los naturales 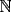 . .Creo que hasta aqui vamos bien.  |
|
|
|
 Jan 24 2007, 01:51 AM Jan 24 2007, 01:51 AM
Publicado:
#2
|
|
 Dios Matemático Supremo Grupo: Moderador Mensajes: 765 Registrado: 25-November 05 Desde: Algun lugar de la V region Miembro Nº: 415 Nacionalidad:  Colegio/Liceo:  Universidad:  Sexo:  |
I CONCEPTO DE NUMERO NATURAL Si hablamos de Numero Natural alguien podría poner 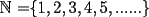 Sin embargo, si queremos ponernos rigurosos, la definición anterior es totalmente ambigua. Por un lado, si queremos presentar el concepto de número natural a un niño, y le mostramos lo anteriormente escrito, el menor tendrá múltiples dudas. No sabrá que número viene después del 5, no sabrá si se repiten números, no sabrá si el orden importa, ni si la serie termina en algún momento. La pregunta que nos debemos hacer entonces es: ¿Cómo formalizamos a los Números Naturales? Se entiende que todos los aspectos señalados deben quedar sumamente claros. Para hacernos alguna idea de la formalización, recordemos algunas características de los números naturales. Son estas características las que toma Giuseppe Peano para plantear sus 5 axiomas de construcción de los números naturales.  |
|
|
|
 Jan 24 2007, 07:11 PM Jan 24 2007, 07:11 PM
Publicado:
#3
|
|
 Dios Matemático Supremo Grupo: Moderador Mensajes: 765 Registrado: 25-November 05 Desde: Algun lugar de la V region Miembro Nº: 415 Nacionalidad:  Colegio/Liceo:  Universidad:  Sexo:  |
II AXIOMAS DE PEANO Y LA INDUCCION MATEMATICA Pero .......... ¿Qué es un Axioma? Diremos que un axioma es una "necesidad logica" Se dice que son una necesidad lógica, pues como todo debe ser justificado, no se puede retroceder infinitamente en el razonamiento: es necesario elegir algunos hechos para que a partir de ellos se puedan demostrar todos los demás. De esta manera, como intento de formalización del concepto de número natural, tenemos que los Axiomas de Peano son los siguientes: Axioma 1 1 es un número natural. (es decir, el conjunto de los números naturales es no vacío) Axioma 2 Si a es un número natural, entonces a+1 también es un número natural (llamado el sucesor de a). Axioma 3 1 no es sucesor de ningún número natural. (primer elemento del conjunto) Axioma 4 Si hay dos números naturales a y b tales que sus sucesores son diferentes entonces a y b son números naturales diferentes. Axioma 5 Si un conjunto de números naturales contiene al 1 y a los sucesores de cada uno de sus elementos entonces contiene a todos los números naturales. Si bien podemos construir toda la teoría de números en base a estos 5 axiomas, nosotros nos quedaremos con el último, al cual llamaremos Axioma de Inducción. El Axioma 5 nos indica las condiciones para que un conjunto de números sea igual al conjunto de los números naturales. Pero además, podemos hacer otra interpretación de éste y decir: “Toda propiedad perteneciente a 1 y al sucesor inmediato de todo número que también tenga esa propiedad pertenece a todos los números.” De esta manera, podemos probar si una propiedad es verdadera o falsa para los números naturales. Resumiendo el Principio de Inducción Matemática es un método de demostración válido para subconjuntos infinitos de numeros naturales. Se basa en los Axiomas de Peano que afirman:  <span style='color:blue'>El Principio de Inducción Matemática es el siguiente:</span> Una proposición P(n) es verdadera para todos los valores de la variable "n" si se cumplen las siguientes condiciones: o bien P(1) es verdadera. donde k es un número natural cualquiera. o bien, p(k) verdadera 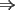 P(k+1) verdadera P(k+1) verdaderaEntonces la proposicion P(n) se cumple para todo número natural n.  |
|
|
|
 Jan 25 2007, 02:30 AM Jan 25 2007, 02:30 AM
Publicado:
#4
|
|
 Dios Matemático Supremo Grupo: Moderador Mensajes: 765 Registrado: 25-November 05 Desde: Algun lugar de la V region Miembro Nº: 415 Nacionalidad:  Colegio/Liceo:  Universidad:  Sexo:  |
EJERCITACION PROBLEMA 1  |
|
|
|
 Jan 25 2007, 03:23 PM Jan 25 2007, 03:23 PM
Publicado:
#5
|
|
 Dios Matemático Supremo Grupo: Moderador Mensajes: 765 Registrado: 25-November 05 Desde: Algun lugar de la V region Miembro Nº: 415 Nacionalidad:  Colegio/Liceo:  Universidad:  Sexo:  |
PROBLEMA 2  |
|
|
|
 Jan 25 2007, 04:23 PM Jan 25 2007, 04:23 PM
Publicado:
#6
|
|
 Dios Matemático Supremo Grupo: Moderador Mensajes: 765 Registrado: 25-November 05 Desde: Algun lugar de la V region Miembro Nº: 415 Nacionalidad:  Colegio/Liceo:  Universidad:  Sexo:  |
PROBLEMA 3  |
|
|
|
 Jan 26 2007, 12:41 AM Jan 26 2007, 12:41 AM
Publicado:
#7
|
|
 Dios Matemático Supremo Grupo: Moderador Mensajes: 765 Registrado: 25-November 05 Desde: Algun lugar de la V region Miembro Nº: 415 Nacionalidad:  Colegio/Liceo:  Universidad:  Sexo:  |
PROBLEMA 4  |
|
|
|
 Jan 26 2007, 12:42 AM Jan 26 2007, 12:42 AM
Publicado:
#8
|
|
 Dios Matemático Supremo Grupo: Moderador Mensajes: 765 Registrado: 25-November 05 Desde: Algun lugar de la V region Miembro Nº: 415 Nacionalidad:  Colegio/Liceo:  Universidad:  Sexo:  |
PROBLEMA 5  |
|
|
|
 Jan 26 2007, 12:43 AM Jan 26 2007, 12:43 AM
Publicado:
#9
|
|
 Dios Matemático Supremo Grupo: Moderador Mensajes: 765 Registrado: 25-November 05 Desde: Algun lugar de la V region Miembro Nº: 415 Nacionalidad:  Colegio/Liceo:  Universidad:  Sexo:  |
PROBLEMA 6  |
|
|
|
 Feb 6 2007, 11:56 PM Feb 6 2007, 11:56 PM
Publicado:
#10
|
|
 Dios Matemático Supremo Grupo: Moderador Mensajes: 765 Registrado: 25-November 05 Desde: Algun lugar de la V region Miembro Nº: 415 Nacionalidad:  Colegio/Liceo:  Universidad:  Sexo:  |
PROBLEMA 7  |
|
|
|
  |
1 usuario(s) está(n) leyendo esta discusión (1 invitado(s) y 0 usuario(s) anónimo(s))
0 miembro(s):
| Versión Lo-Fi | Fecha y Hora actual: 3rd April 2025 - 04:30 PM |















