|
|
|
|
|
|
|
  |
 Jan 23 2007, 04:46 PM Jan 23 2007, 04:46 PM
Publicado:
#1
|
|
 Dios Matemático Supremo Grupo: Colaborador Silver Mensajes: 725 Registrado: 17-July 05 Desde: Puente Alto-Santiago Miembro Nº: 148 Nacionalidad:  Universidad:  Sexo:  |
 ![TEX: \[<br />\begin{gathered}<br /> \text{Cu\'anto tiempo tardar\'a en llenarse por completo un vaso de forma c\'onica}\text{, } \hfill \\<br /> \text{colocado bajo un grifo que vierte agua de manera constante}\text{, si se llena hasta } \hfill \\<br /> \text{la cuarta parte de su altura en un minuto?} \hfill \\ <br />\end{gathered} <br />\]<br />](./tex/1169588799.gif)
-------------------- "Resolver un problema es una meta específica de la inteligencia e inteligencia es el don específico de los seres humanos: Resolver un problema es la actividad humana por excelencia"
  |
|
|
|
 Jul 11 2014, 05:38 PM Jul 11 2014, 05:38 PM
Publicado:
#2
|
|
 Dios Matemático Grupo: Usuario FMAT Mensajes: 325 Registrado: 18-March 14 Miembro Nº: 127.725 Nacionalidad:  Colegio/Liceo:  Universidad:  Sexo:  |
Digamos que el vaso de forma cónica tiene radio basal R y altura H.
Si está lleno hasta la cuarta parte podriamos decir que tiene 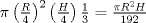 de agua. de agua.Luego 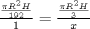 Y tenemos que 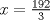 osea 64 min osea 64 min
|
|
|
|
  |
1 usuario(s) está(n) leyendo esta discusión (1 invitado(s) y 0 usuario(s) anónimo(s))
0 miembro(s):
| Versión Lo-Fi | Fecha y Hora actual: 4th April 2025 - 05:03 AM |








