PEP I - Foro fmat.cl

Portal Matemático

¿Qué es FMAT?

Foro fmat.cl > Programa Enseñanza Universitaria > Comunidades Universitarias > Universidad de Santiago de Chile > Matemática General

2 Páginas:

1 2 >

Reply to this topic

Start new topic

PEP I

Zephyr~ Ver Perfil del Miembro Ver los mensajes de este miembro	Oct 29 2010, 04:58 PM Publicado: #1
Dios Matemático Supremo Grupo: Usuario FMAT Mensajes: 1.065 Registrado: 24-November 08 Desde: In my Crazy Mind ♫~ Miembro Nº: 39.334 Nacionalidad: Colegio/Liceo: Universidad: Sexo:	$TEX: \begin{center}<br />PRIMERA PRUEBA PEP MATEMATICA II\\<br />Ingeniería comercial\\<br />\end{center}<br />\begin{enumerate}<br />\item Verificar si la función $y^2=4e^{2x}-3$ satisface la ecuación:\\<br />\begin{center}$y \cdot y'' + (y')^2-2y \cdot y'=0$<br />\end{center}<br />\item Sea $f$ una función de veriables reales definida por:<br />\\<br />\begin{center}$f(x)=\frac{x}{(x+1)^2}$<br />\end{center}<br />i)Determinar intervalos de crecimiento y decrecimiento.\\<br />ii)Obtener valores mácimos y/o mínimos.\\<br />iii)Obtener concavidad y puntos de inflexión.\\<br />iv)Bosquejar gráfico\\<br />\\<br />\item Resolver usando L'Hopital:\\<br />\begin{center}$\displaystyle \lim_{x\rightarrow 0}\left( \dfrac{1}{x} \right)^{senx}$<br />\end{center}<br />\item La ecuación de demanda de cierta mercancía cuando se ha producido $q$ unidades es $P+3q^2-1200=0$.Si el costo total de producción de estas $q$ unidades está dado por $C(q)=5q^2+200q-150$.\\<br />\\<br />i)Calcular el número de unidades que se deben producir para maximizar la utilidad.\\<br />ii)Calcular la respectiva utilidad total.\\<br />\\<br />\item Desarrollar:<br />\begin{center} $I=\displaystyle \int \dfrac{x^9}{\sqrt{x^5+1}}dx$<br />\end{center}<br />\end{enumerate}$ Mensaje modificado por Zephyr~ el Oct 29 2010, 04:59 PM -------------------- and User

Zephyr~ Ver Perfil del Miembro Ver los mensajes de este miembro	Oct 29 2010, 05:02 PM Publicado: #2
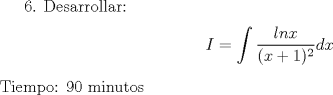
Dios Matemático Supremo Grupo: Usuario FMAT Mensajes: 1.065 Registrado: 24-November 08 Desde: In my Crazy Mind ♫~ Miembro Nº: 39.334 Nacionalidad: Colegio/Liceo: Universidad: Sexo:	$TEX: <br />6. Desarrollar:<br />\begin{center} $I=\displaystyle \int \dfrac{lnx}{(x+1)^2}dx$<br />\end{center}<br />Tiempo: 90 minutos<br />$ -------------------- and User

fabiannx15 Ver Perfil del Miembro Ver los mensajes de este miembro	Oct 29 2010, 06:24 PM Publicado: #3
Dios Matemático Supremo Grupo: Usuario FMAT Mensajes: 2.169 Registrado: 11-June 08 Desde: rancagua Miembro Nº: 26.922 Nacionalidad: Colegio/Liceo: Universidad: Sexo:	P.3 $TEX: \[<br />\begin{gathered}<br /> e^{ - \left[ {\frac{{\ln x}}<br />{{\frac{1}<br />{{senx}}}}} \right]\frac{{\frac{d}<br />{{dx}}}}<br />{{\frac{d}<br />{{dx}}}}} \hfill \\<br /> = e^{\frac{{ - 1}}<br />{{x\cos ^2 x}}} \hfill \\<br /> = e^{\frac{{ - 1\frac{d}<br />{{dx}}}}<br />{{x\cos ^2 x\frac{d}<br />{{dx}}}}} \hfill \\<br /> = e^{\frac{0}<br />{{\cos ^2 x - 2xsenx}}} \Rightarrow x \to 0\frac{0}<br />{{\cos ^2 x - 2xsenx}} = \frac{0}<br />{{1 - 0}} = 0\therefore \mathop {\lim }\limits_{x \to 0} \left( {\frac{1}<br />{x}} \right)^{senx} = 1 \hfill \\ <br />\end{gathered} <br />\]<br />$ -------------------- Richard Fabian Jerez Ex alumno del Liceo Oscar Castro 4ºL matemático Estudiante Ingeniería Civil Mecánica USM ¿Necesitas ayuda para la psu y no tienes dinero?: Agrega a logratus850@hotmail.com y comienza a preguntar! Somos un grupo de universitarios dispuestos a ayudarte de manera gratuita para que logres tus sueños, todos tuvimos como promedio más de 800 puntos en la PSU. Team PSU 2010!! Únete! [color="#000080"][/color]

Uchiha Itachi Ver Perfil del Miembro Ver los mensajes de este miembro	Oct 29 2010, 06:29 PM Publicado: #4
Staff FMAT Grupo: Super Moderador Mensajes: 4.857 Registrado: 2-January 08 Miembro Nº: 14.268 Nacionalidad: Colegio/Liceo: Universidad: Sexo:	$TEX: % MathType!MTEF!2!1!+-<br />% feaagaart1ev2aaatCvAUfeBSjuyZL2yd9gzLbvyNv2CaerbuLwBLn<br />% hiov2DGi1BTfMBaeXatLxBI9gBaerbd9wDYLwzYbItLDharqqtubsr<br />% 4rNCHbGeaGqiVu0Je9sqqrpepC0xbbL8F4rqqrFfpeea0xe9Lq-Jc9<br />% vqaqpepm0xbba9pwe9Q8fs0-yqaqpepae9pg0FirpepeKkFr0xfr-x<br />% fr-xb9adbaqaaeGaciGaaiaabeqaamaabaabaaGceaqabeaadaqjEa<br />% qaaiaabofacaqGqbGaaeymaaaaaeaacaWG5bWaaWbaaSqabeaacaaI<br />% YaaaaOGaeyypa0JaaGinaiaadwgadaahaaWcbeqaaiaaikdacaWG4b<br />% aaaOGaeyOeI0IaaG4maiabgkDiElaaikdacaWG5bGabmyEayaafaGa<br />% eyypa0JaaGioaiaadwgadaahaaWcbeqaaiaaikdacaWG4baaaOGaey<br />% O0H4TaamyEaiqadMhagaqbgaqbaiabgUcaRmaabmaabaGabmyEayaa<br />% faaacaGLOaGaayzkaaWaaWbaaSqabeaacaaIYaaaaOGaeyypa0JaaG<br />% ioaiaadwgadaahaaWcbeqaaiaaikdacaWG4baaaaGcbaaabaGaaeit<br />% aiaabwhacaqGLbGaae4zaiaab+gacaqGGaGaaeOoaiaabccaaeaaae<br />% aacaWG5bGaeyyXICTabmyEayaafyaafaGaey4kaSYaaeWaaeaaceWG<br />% 5bGbauaaaiaawIcacaGLPaaadaahaaWcbeqaaiaaikdaaaGccqGHsi<br />% slcaaIYaGaamyEaiqadMhagaqbaiabg2da9iaaiIdacaWGLbWaaWba<br />% aSqabeaacaaIYaGaamiEaaaakiabgkHiTiaaiIdacaWGLbWaaWbaaS<br />% qabeaacaaIYaGaamiEaaaakiabg2da9iaaicdaaeaaaeaacaqGqbGa<br />% ae4BaiaabkhacaqGGaGaaeiDaiaabggacaqGUbGaaeiDaiaab+gaca<br />% qGGaGaamyEamaaCaaaleqabaGaaGOmaaaakiabg2da9iaaisdacaWG<br />% LbWaaWbaaSqabeaacaaIYaGaamiEaaaakiabgkHiTiaaiodacaqGGa<br />% Gaae4CaiaabggacaqG0bGaaeyAaiaabohacaqGMbGaaeyyaiaaboga<br />% caqGLbGaaeiiaiaabYgacaqGHbGaaeiiaiaabwgacaqGJbGaaeyDai<br />% aabggacaqGJbGaaeyAaiaab+gacaqGUbGaaeiiaiaabsgacaqGPbGa<br />% aeOzaiaabwgacaqGYbGaaeyzaiaab6gacaqGJbGaaeyAaiaabggaca<br />% qGSbGaaeOlaaaaaa!A5C5!<br />\[<br />\begin{gathered}<br /> \boxed{{\text{SP1}}} \hfill \\<br /> y^2 = 4e^{2x} - 3 \Rightarrow 2yy' = 8e^{2x} \Rightarrow yy'' + \left( {y'} \right)^2 = 8e^{2x} \hfill \\<br /> \hfill \\<br /> {\text{Luego : }} \hfill \\<br /> \hfill \\<br /> y \cdot y'' + \left( {y'} \right)^2 - 2yy' = 8e^{2x} - 8e^{2x} = 0 \hfill \\<br /> \hfill \\<br /> {\text{Por tanto }}y^2 = 4e^{2x} - 3{\text{ satisface la ecuacion diferencial}}{\text{.}} \hfill \\ <br />\end{gathered} <br />\]$ -------------------- Candidato a doctor en Cs. De la ingeniería mención modelamiento matemático, DIM. Universidad de Chile Magíster en ciencias mención matemática, Profesor de estado en matemáticas y computación, Licenciado en educación matemáticas y computación, USACH

Uchiha Itachi Ver Perfil del Miembro Ver los mensajes de este miembro	Oct 29 2010, 06:32 PM Publicado: #5
Staff FMAT Grupo: Super Moderador Mensajes: 4.857 Registrado: 2-January 08 Miembro Nº: 14.268 Nacionalidad: Colegio/Liceo: Universidad: Sexo:	$TEX: % MathType!MTEF!2!1!+-<br />% feaagaart1ev2aaatCvAUfeBSjuyZL2yd9gzLbvyNv2CaerbuLwBLn<br />% hiov2DGi1BTfMBaeXatLxBI9gBaerbd9wDYLwzYbItLDharqqtubsr<br />% 4rNCHbGeaGqiVu0Je9sqqrpepC0xbbL8F4rqqrFfpeea0xe9Lq-Jc9<br />% vqaqpepm0xbba9pwe9Q8fs0-yqaqpepae9pg0FirpepeKkFr0xfr-x<br />% fr-xb9adbaqaaeGaciGaaiaabeqaamaabaabaaGceaqabeaadaqjEa<br />% qaaiaabofacaqGqbGaaeynaaaaaeaacaqGtbGaaeyzaiaabggacaqG<br />% GaGaaeiiaiaadwhadaahaaWcbeqaaiaaikdaaaGccqGH9aqpcaWG4b<br />% WaaWbaaSqabeaacaaI1aaaaOGaey4kaSIaaGymaiabgkDiElaaikda<br />% caWG1bGaamizaiaadwhacqGH9aqpcaaI1aGaamiEamaaCaaaleqaba<br />% GaaGinaaaakiaadsgacaWG4bGaaeiiaiaabYcacaqGGaGaaeOBaiaa<br />% b+gacaqG0bGaaeyyaiaab6gacaqGKbGaae4BaiaabccacaqGHbGaae<br />% izaiaabwgacaqGTbGaaeyyaiaabohacaqGGaGaaeyCaiaabwhacaqG<br />% LbGaaeiiaiaabQdacaqGGaWaaSaaaeaacaWG4bWaaWbaaSqabeaaca<br />% aI5aaaaaGcbaWaaOaaaeaacaWG4bWaaWbaaSqabeaacaaI1aaaaOGa<br />% ey4kaSIaaGymaaWcbeaaaaGccqGH9aqpdaWcaaqaaiaadIhadaahaa<br />% WcbeqaaiaaiwdaaaGccqGHflY1caWG4bWaaWbaaSqabeaacaaI0aaa<br />% aaGcbaWaaOaaaeaacaWG4bWaaWbaaSqabeaacaaI1aaaaOGaey4kaS<br />% IaaGymaaWcbeaaaaGccaqGGaGaaeilaiaabccacaqGWbGaae4Baiaa<br />% bkhacaqGGaGaaeiDaiaabggacaqGUbGaaeiDaiaab+gacaqGGaGaae<br />% OoaaqaaiaadMeacqGH9aqpdaWdbaqaamaalaaabaGaaGOmamaabmaa<br />% baGaamyDamaaCaaaleqabaGaaGOmaaaakiabgkHiTiaaigdaaiaawI<br />% cacaGLPaaacaWG1bGaamizaiaadwhaaeaacaaI1aGaamyDaaaaaSqa<br />% beqaniabgUIiYdGccqGH9aqpdaWcaaqaaiaaikdaaeaacaaI1aaaam<br />% aapeaabaGaamyDamaaCaaaleqabaGaaGOmaaaakiabgkHiTiaaigda<br />% caWGKbGaamyDaaWcbeqab0Gaey4kIipakiabg2da9maalaaabaGaaG<br />% OmaiaadwhadaahaaWcbeqaaiaaiodaaaaakeaacaaIXaGaaGynaaaa<br />% cqGHsisldaWcaaqaaiaadwhadaahaaWcbeqaaiaaikdaaaaakeaaca<br />% aI1aaaaiabgUcaRiaadoeaaeaaaeaacaqGbbGaae4CaiaabMgacaqG<br />% GaGaaeOoaiaabccacaqGGaGaamysaiabg2da9maalaaabaGaaGOmam<br />% aabmaabaGaamiEamaaCaaaleqabaGaaGynaaaakiabgUcaRiaaigda<br />% aiaawIcacaGLPaaadaGcaaqaaiaadIhadaahaaWcbeqaaiaaiwdaaa<br />% GccqGHRaWkcaaIXaaaleqaaaGcbaGaaGymaiaaiwdaaaGaeyOeI0Ya<br />% aSaaaeaacaWG4bWaaWbaaSqabeaacaaI1aaaaOGaey4kaSIaaGymaa<br />% qaaiaaiwdaaaGaey4kaSIaam4qaaaaaa!BB0F!<br />\[<br />\begin{gathered}<br /> \boxed{{\text{SP5}}} \hfill \\<br /> {\text{Sea }}u^2 = x^5 + 1 \Rightarrow 2udu = 5x^4 dx{\text{ }}{\text{, notando ademas que : }}\frac{{x^9 }}<br />{{\sqrt {x^5 + 1} }} = \frac{{x^5 \cdot x^4 }}<br />{{\sqrt {x^5 + 1} }}{\text{ }}{\text{, por tanto :}} \hfill \\<br /> I = \int {\frac{{2\left( {u^2 - 1} \right)udu}}<br />{{5u}}} = \frac{2}<br />{5}\int {u^2 - 1du} = \frac{{2u^3 }}<br />{{15}} - \frac{{u^2 }}<br />{5} + C \hfill \\<br /> \hfill \\<br /> {\text{Asi : }}I = \frac{{2\left( {x^5 + 1} \right)\sqrt {x^5 + 1} }}<br />{{15}} - \frac{{x^5 + 1}}<br />{5} + C \hfill \\ <br />\end{gathered} <br />\]$ -------------------- Candidato a doctor en Cs. De la ingeniería mención modelamiento matemático, DIM. Universidad de Chile Magíster en ciencias mención matemática, Profesor de estado en matemáticas y computación, Licenciado en educación matemáticas y computación, USACH

Zephyr~ Ver Perfil del Miembro Ver los mensajes de este miembro	Nov 12 2010, 10:59 AM Publicado: #6
Dios Matemático Supremo Grupo: Usuario FMAT Mensajes: 1.065 Registrado: 24-November 08 Desde: In my Crazy Mind ♫~ Miembro Nº: 39.334 Nacionalidad: Colegio/Liceo: Universidad: Sexo:	$TEX: \noindent<br /><br /> \boxed{{\text{SP4}}} \hfill \\<br />\\<br />i)Primero, debemos determinar la función de utilidad que se encuentra dada por $U(q)= I(q)-C(q)$\\<br />\\<br />Como $I(q)=P \cdot q$ Despejaremos p de la ecuación de demanda, luego:\\<br />$P=-3q^2+1200$, por lo tanto $I(q)=-3q^3+1200q$. Con esto, podemos determinar la función de utilidad:\\<br />\\<br />$U(q)=-3q^3+1200q-5q^2-200q+150$\\<br />$U(q)=-3q^3-5q^2+1000q+150$\\<br />\\<br />Derivando la utilidad obtenemos que:\\<br />$U'(q)=-9q^2-10q+1000$\\<br />\\<br />Igualando a 0:\\<br />\\<br />$-9q^2-10q+1000=0$\\<br />\\<br />$9q^2+10q-1000=0$\\<br />\\<br />$(q-10)(9q+100)=0$\\<br />\\<br />Dado que las unidades son positivas, utilizaremos $q=10$.\\<br />Usando el criterio de la segunda derivada:\\<br />$U''(q)=-18q-10$\\<br />$U''(10)<0$ Por lo tanto, 10 es un máximo.\\<br />\\<br />Finalmente, concluimos que 10 unidades maximizan la utilidad.\\<br />\\<br />ii)Evaluando en la función de utilidad:\\<br />\\<br />$U(10)=-3(10)^3-5(10)^2+1000(10)+150=-3500+10150=6650$\\<br />\\<br />Por lo cual, la utilidad total es 6650 unidades monetarias.<br /><br /><br />$ -------------------- and User

Zephyr~ Ver Perfil del Miembro Ver los mensajes de este miembro	Dec 24 2010, 04:47 PM Publicado: #7
Dios Matemático Supremo Grupo: Usuario FMAT Mensajes: 1.065 Registrado: 24-November 08 Desde: In my Crazy Mind ♫~ Miembro Nº: 39.334 Nacionalidad: Colegio/Liceo: Universidad: Sexo:	$TEX: \noindent<br /><br /> \boxed{{\text{SP6}}} \hfill \\<br />\\<br />Usando Integración por partes:\\<br />\\<br />$u=ln(x)$\\<br />$du=\dfrac{dx}{x}$\\<br />$dv=\dfrac{dx}{(1+x)^2}$\\<br />\\<br />$v=\dfrac{-1}{(1+x)}$\\<br />\\<br />$I=\displaystyle \int \dfrac{ln(x)}{(x+1)^2}dx=\dfrac{-ln(x)}{(1+x)}+ \displaystyle \int \dfrac{1}{x(x+1)}dx$\\<br />\\<br />$I_{2}=\displaystyle \int \dfrac{1}{x(x+1)}dx=\int {\dfrac{1}{x}-\dfrac{1}{(x+1)} dx}=ln(x)-ln(x+1)$\\<br />\\<br />Finalmente:<br />$I=\displaystyle \int \dfrac{lnx}{(x+1)^2}dx=\dfrac{-ln(x)}{(1+x)}+ln(x)-ln(x+1)+C$<br />$ Espero no haberme equivocado xd PD: Me falta la PEP II Mensaje modificado por Zephyr~ el Dec 24 2010, 05:00 PM -------------------- and User

Shine Ver Perfil del Miembro Ver los mensajes de este miembro	Dec 24 2010, 04:58 PM Publicado: #8
Dios Matemático Supremo Grupo: Usuario FMAT Mensajes: 1.255 Registrado: 22-February 08 Miembro Nº: 15.777 Sexo:	CITA(Zephyr~ @ Dec 24 2010, 06:47 PM) $TEX: \noindent<br /><br /> \boxed{{\text{SP6}}} \hfill \\<br />\\<br />Usando Integración por partes:\\<br />\\<br />$u=ln(x)$\\<br />$du=\dfrac{dx}{x}$\\<br />$dv=\dfrac{dx}{(1+x)^2}$\\<br />\\<br />$v=\dfrac{-1}{(1+x)}$\\<br />\\<br />$I=\displaystyle \int \dfrac{ln(x)}{(x+1)^2}dx=\dfrac{ln(x)}{(1+x)}+ \displaystyle \int \dfrac{1}{x(x+1)}dx$\\<br />\\<br />$I_{2}=\displaystyle \int \dfrac{1}{x(x+1)}dx=\int {\dfrac{1}{x}-\dfrac{1}{(x+1)} dx}=ln(x)-ln(x+1)$\\<br />\\<br />Finalmente:<br />$I=\displaystyle \int \dfrac{lnx}{(x+1)^2}dx=\dfrac{ln(x)}{(1+x)}+ln(x)-ln(x+1)+C$<br />$ Espero no haberme equivocado xd PD: Me falta la PEP II En la primera parte de la integral, cuando haces la integración por partes, el uv te queda ln(x) / (x+1) ... no le falta un signo menos?

Zephyr~ Ver Perfil del Miembro Ver los mensajes de este miembro	Dec 24 2010, 04:59 PM Publicado: #9
Dios Matemático Supremo Grupo: Usuario FMAT Mensajes: 1.065 Registrado: 24-November 08 Desde: In my Crazy Mind ♫~ Miembro Nº: 39.334 Nacionalidad: Colegio/Liceo: Universidad: Sexo:	CITA(Shine @ Dec 24 2010, 06:58 PM) En la primera parte de la integral, cuando haces la integración por partes, el uv te queda ln(x) / (x+1) ... no le falta un signo menos? Sí :B gracias por la acotación ! PD: Se nota que estoy en vacaciones -------------------- and User

Ditox Ver Perfil del Miembro Ver los mensajes de este miembro	Dec 24 2010, 05:53 PM Publicado: #10
Dios Matemático Supremo Grupo: Usuario FMAT Mensajes: 2.039 Registrado: 4-October 09 Desde: Valparaíso Miembro Nº: 59.794 Nacionalidad: Colegio/Liceo: Universidad: Sexo:	Hare el del gráfico, pero dejaré al lector el trabajo algebraico. La función es $TEX: \[f(x)=\frac{x}{(x+1)^2}\]$ , notemos que su dominio es $TEX: \[\mathbb{R}-\left \{ -1 \right \}\]$ , luego tiene una asintota vertical de ecuación x=-1 , además es fácil ver que su única raíz es en x=0 , y además f(0)=0 por tanto pasa por el origen. Si calculamos alguna asintota horizontal vemos que $TEX: \[\lim_{x\rightarrow \infty }\frac{x}{(x+1)^2}=0\]$ , por tanto se concluye que la funcion es asintotica al eje de las abscisas. Ahora notemos que $TEX: \[f'(x)=\frac{1-x}{(x+1)^3}\]$ , por tanto los posibles candidatos a puntos críticos son1 y -1 Si vemos tambien que $TEX: \[f''(x)=\frac{2(x-2)}{(x+1)^4}\]$ notamos que los puntos de Inflexion son en 2 y en -1 En resumen: Puntos críticos: -1 y 1 Puntos de inflexión: 2 Con esto ya podmeos estudiar el crecimiento viendo f`(x) $TEX: \[x\in (-\infty ,-1)\]$ Decrece (desde 0 hasta -inf) $TEX: \[x\in (-1 , 1)\]$ Crece(desde -inf hasta f(1) $TEX: \[x\in (1,+\infty )\]$ Decrece (desde f(1) hasta 0) Por tanto tiene un MAXIMO Relativo en (1,f(1)) = (1,1/4) Mínimo absoluto en (-1 ,-inf) Tambien podemos ver la concavidad de f con f''(x) $TEX: \[f''(x)=\frac{2(x-2)}{(x+1)^4}> 0\: \Rightarrow x-2> 0\: \Leftrightarrow x> 2\]$ Luego Si: $TEX: \[x\in (-\infty ,2)\]$ Concava hacia abajo $TEX: \[x\in (2,+\infty)\]$ Concava hacia arriba Finalmente el gráfico de la susodicha es: Archivo(s) Adjunto(s) MSP203719deh625c0hb3dh10000184aiifb891i8dig.gif ( 3.07k ) Número de descargas: 1 --------------------

« Posterior · Matemática General · Anterior »

2 Páginas:

1 2 >

Reply to this topic

Start new topic

1 usuario(s) está(n) leyendo esta discusión (1 invitado(s) y 0 usuario(s) anónimo(s))

0 miembro(s):

Modo de Ver: Estándar · Cambiar a: Lineal+ · Cambiar a: Outline

Suscribirse · Enviar por correo · Imprimir · Suscribirse a este foro

Versión Lo-Fi

Fecha y Hora actual: 18th February 2025 - 05:41 PM

Powered By IP.Board 2.2.1 © 2007 IPS, Inc.