Control 2 2010/02 Ortega/Cominnetti - Foro fmat.cl

Portal Matemático

¿Qué es FMAT?

Foro fmat.cl > Programa Enseñanza Universitaria > Comunidades Universitarias > Universidad de Chile > Cálculo Avanzado

Reply to this topic

Start new topic

Control 2 2010/02 Ortega/Cominnetti, Variable Compleja

Crash! Ver Perfil del Miembro Ver los mensajes de este miembro	Oct 28 2010, 09:56 PM Publicado: #1
Dios Matemático Supremo Grupo: Usuario FMAT Mensajes: 929 Registrado: 22-June 08 Desde: Santiago Miembro Nº: 27.979 Nacionalidad: Colegio/Liceo: Universidad: Sexo:	$TEX: \[\begin{gathered}<br /> \left. {\underline {\, <br /> {{\text{P1}}} \,}}\! \right\| \hfill \\<br /> {\text{a) (2 ptos) Resuelva la ecuacion: }}{e^z} = \cos \left( {iz} \right) \hfill \\<br /> \hfill \\<br /> {\text{b) (2 ptos) Determine el conjunto A de todos los }}z \in \mathbb{C}{\text{ donde}} \hfill \\<br /> f\left( z \right) = z - i{\left\| z \right\|^2} + \Re e\left( z \right){\left( {\Im m\left( z \right)} \right)^2} \hfill \\<br /> \hfill \\<br /> {\text{c) (2 ptos) Determinar las funciones de variable real }}s\left( y \right),\;t\left( y \right),{\text{ diferenciables}} \hfill \\<br /> \left( {{\text{en }}\mathbb{R}} \right){\text{ tales que }}s\left( 0 \right) = 1,\;t\left( 0 \right) = 0{\text{ de modo que la funcion compleja}} \hfill \\<br /> f\left( {x + iy} \right) = {e^x}\left( {s\left( y \right) + it\left( y \right)} \right) \hfill \\<br /> {\text{sea holomorfa}}{\text{.}} \hfill \\<br /> {\text{Indicacion: Recordar que }}u''\left( r \right) + {a^2}u\left( r \right) = 0{\text{ tiene como solucion general}} \hfill \\<br /> u\left( r \right) = \alpha \sin \left( {ar} \right) + \beta \cos \left( {ar} \right). \hfill \\ <br />\end{gathered} \]<br />$ $TEX: \[\begin{gathered}<br /> \left. {\underline {\, <br /> {{\text{P2}}} \,}}\! \right\| \hfill \\<br /> {\text{a) (4 ptos) Sea }}p\left( z \right) = \sum\limits_{k = 0}^n {{c_k}{{\left( {z - {z_0}} \right)}^k}} {\text{ un polinomio de grado }}n{\text{ para }}{z_0} \in \mathbb{C}. \hfill \\<br /> {\text{Demuestre que se cumple}} \hfill \\<br /> \oint\limits_\gamma {p\left( z \right)d\bar z} = - 2\pi ip'\left( {{z_0}} \right){a^2} = - {a^2}\oint\limits_\gamma {\frac{{p'\left( z \right)}}<br />{{z - {z_0}}}dz} \hfill \\<br /> {\text{donde }}\gamma :\left\| {z - {z_0}} \right\| = a,{\text{ con }}a > 0. \hfill \\<br /> {\text{Nota: }}\oint\limits_\gamma {p\left( z \right)d\bar z} = \int\limits_c^d {f\left( {g\left( t \right)} \right)\overline {g'\left( t \right)} dt} ,{\text{ donde }}g:\left[ {c,d} \right] \to \mathbb{C}{\text{ es una parametrizacion de }}\gamma {\text{.}} \hfill \\<br /> {\text{Indicacion: Recuerde que }}{c_k} = \frac{{{p^{\left( k \right)}}\left( {{z_0}} \right)}}<br />{{k!}} \hfill \\<br /> \hfill \\<br /> {\text{b) (2 ptos) Calcule la integral}} \hfill \\<br /> \oint\limits_\gamma {\frac{{{z^2} + 1 - {e^z}}}<br />{{{z^2}{{\left( {z - 2} \right)}^2}}}dz} , \hfill \\<br /> {\text{donde }}\gamma {\text{ es la circunferencia }}\left\| z \right\| = a{\text{. Separe los casos }}0 < a < 2{\text{ y }}a > 2 \hfill \\ <br />\end{gathered} \]<br />$ $TEX: \[\begin{gathered}<br /> \left. {\underline {\, <br /> {{\text{P3}}} \,}}\! \right\| \hfill \\<br /> {\text{a) (2 ptos) Determine los polos (con sus ordenes) y los correspondientes}} \hfill \\<br /> {\text{residuos de la funcion:}} \hfill \\<br /> f\left( z \right) = \frac{{1 - \cos \left( z \right)}}<br />{{{z^2}\sin \left( z \right)}} \hfill \\<br /> \hfill \\<br /> {\text{b) (2 ptos) Encuentre la serie de Taylor de la funcion}} \hfill \\<br /> f\left( z \right) = \frac{{z + 1}}<br />{{z\left( {z + 5} \right)}} \hfill \\<br /> {\text{en torno al punto }}{z_0} = i{\text{ y determine el radio de convergencia}}{\text{.}} \hfill \\<br /> {\text{Indicacion: Puede ser util usar una descomposicion en fracciones parciales}}{\text{.}} \hfill \\<br /> \hfill \\<br /> {\text{c) (2 ptos) Sea }}g{\text{ holomorfa en }}0{\text{ con }}g\left( 0 \right) \ne 0{\text{ y }}f\left( z \right) = \frac{{g\left( z \right)}}<br />{{{z^k}}},{\text{ con }}k \in \mathbb{N}\backslash \left\{ 0 \right\}. \hfill \\<br /> {\text{Pruebe que }}p = 0{\text{ es un polo de }}\frac{{f'\left( z \right)}}<br />{{f\left( z \right)}}.{\text{ Determine su orden y calcule su residuo}}{\text{.}} \hfill \\<br /> \hfill \\<br /> \left. {\underline {\, <br /> {{\text{Tiempo: 3 Horas}}} \,}}\! \right\| \hfill \\ <br />\end{gathered} \]<br />$ Comentario personal: Costó pero salió -------------------- Ex-Electrico Usach 2008 Mechón Injenieria 2009 Tengo Sed.

Krebante Ver Perfil del Miembro Ver los mensajes de este miembro	Oct 30 2010, 07:37 AM Publicado: #2
Dios Matemático Supremo Grupo: Usuario FMAT Mensajes: 618 Registrado: 8-June 08 Desde: Paris Miembro Nº: 26.525 Nacionalidad: Colegio/Liceo: Universidad: Sexo:	P2 a) 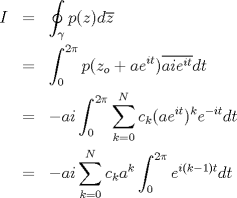$TEX: \begin{eqnarray}<br />I & = & \displaystyle\oint_{\gamma} p(z) d\overline{z} \\<br /> & = & \int_0^{2\pi}p(z_o + ae^{it}) \overline{ai e^{it}}dt \\<br /> & = & -ai \int_0^{2\pi} \sum_{k = 0}^N c_k (a e^{it})^k e^{-it} dt \\<br /> & = & -ai \sum_{k = 0}^N c_k a^k \int_0^{2\pi} e^{i(k-1)t} dt<br />\end{eqnarray}$ Notamos que si 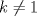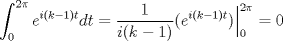$TEX: $k \neq 1$$ , $TEX: $\displaystyle\int_0^{2\pi} e^{i(k-1)t}dt = \frac{1}{i(k-1)}(e^{i(k-1)t}) \Big \|_0^{2\pi} = 0$$ por lo que 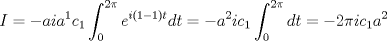$TEX: $\displaystyle I = -ai a^1 c_1 \int_0^{2\pi} e^{i(1-1)t} dt = -a^2i c_1 \int_0^{2\pi} dt = -2\pi i c_1 a^2$$ Además, como 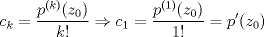$TEX: $c_k = \displaystyle\frac{p^{(k)}(z_0)}{k!} \Rightarrow c_1 = \frac{p^{(1)}(z_0)}{1!} = p'(z_0)$$ con lo que se tiene la primera igualdad. La segunda igualdad es directa de la fórmula de Cauchy. -------------------- ¡Por más representación, vota Riesz!

Crash! Ver Perfil del Miembro Ver los mensajes de este miembro	Oct 30 2010, 09:54 AM Publicado: #3
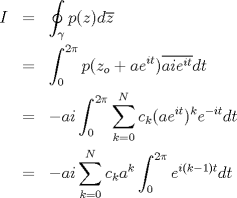Dios Matemático Supremo Grupo: Usuario FMAT Mensajes: 929 Registrado: 22-June 08 Desde: Santiago Miembro Nº: 27.979 Nacionalidad: Colegio/Liceo: Universidad: Sexo:	CITA(Krebante @ Oct 30 2010, 08:37 AM) P2 a) $TEX: \begin{eqnarray}<br />I & = & \displaystyle\oint_{\gamma} p(z) d\overline{z} \\<br /> & = & \int_0^{2\pi}p(z_o + ae^{it}) \overline{ai e^{it}}dt \\<br /> & = & -ai \int_0^{2\pi} \sum_{k = 0}^N c_k (a e^{it})^k e^{-it} dt \\<br /> & = & -ai \sum_{k = 0}^N c_k a^k \int_0^{2\pi} e^{i(k-1)t} dt<br />\end{eqnarray}$ Notamos que si 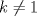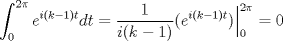$TEX: $k \neq 1$$ , $TEX: $\displaystyle\int_0^{2\pi} e^{i(k-1)t}dt = \frac{1}{i(k-1)}(e^{i(k-1)t}) \Big \|_0^{2\pi} = 0$$ por lo que 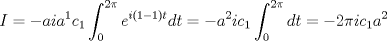$TEX: $\displaystyle I = -ai a^1 c_1 \int_0^{2\pi} e^{i(1-1)t} dt = -a^2i c_1 \int_0^{2\pi} dt = -2\pi i c_1 a^2$$ Además, como 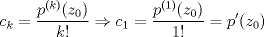$TEX: $c_k = \displaystyle\frac{p^{(k)}(z_0)}{k!} \Rightarrow c_1 = \frac{p^{(1)}(z_0)}{1!} = p'(z_0)$$ con lo que se tiene la primera igualdad. La segunda igualdad es directa de la fórmula de Cauchy. y para k=1? -------------------- Ex-Electrico Usach 2008 Mechón Injenieria 2009 Tengo Sed.

Kaissa Ver Perfil del Miembro Ver los mensajes de este miembro	Oct 30 2010, 10:26 AM Publicado: #4
Dios Matemático Supremo Grupo: Usuario FMAT Mensajes: 9.897 Registrado: 6-April 08 Miembro Nº: 19.238 Nacionalidad: Colegio/Liceo: Sexo:	CITA(Crash! @ Oct 30 2010, 09:54 AM) y para k=1? no seas fome po xd si ese es el caso trivial, integral definida de una cte dara 0. -------------------- Este es un extracto de Qué es fmat by Kenshin. La pregunta para ti estimado(a) lector(a) es... ¿Qué haces tu para que ésto se cumpla?

Crash! Ver Perfil del Miembro Ver los mensajes de este miembro	Oct 30 2010, 11:42 AM Publicado: #5
Dios Matemático Supremo Grupo: Usuario FMAT Mensajes: 929 Registrado: 22-June 08 Desde: Santiago Miembro Nº: 27.979 Nacionalidad: Colegio/Liceo: Universidad: Sexo:	Sorry, pero no se supone que eso mismo no daria cero? xD PD: olvidenme xD Mensaje modificado por Crash! el Oct 30 2010, 12:38 PM -------------------- Ex-Electrico Usach 2008 Mechón Injenieria 2009 Tengo Sed.

galois Ver Perfil del Miembro Ver los mensajes de este miembro	Nov 3 2010, 07:41 PM Publicado: #6
Maestro Matemático Grupo: Usuario FMAT Mensajes: 107 Registrado: 29-October 07 Desde: San Felipe-Santiago Miembro Nº: 11.941 Nacionalidad: Universidad: Sexo:	Hint :Para la 1 c) se puede hacer de dos maneras: una es considerando Cauchy Riemann y la otra es utilizando el llamado principio de identidad. Salu2 Mensaje modificado por galois el Nov 7 2010, 06:26 PM

Crash! Ver Perfil del Miembro Ver los mensajes de este miembro	Nov 3 2010, 08:12 PM Publicado: #7
Dios Matemático Supremo Grupo: Usuario FMAT Mensajes: 929 Registrado: 22-June 08 Desde: Santiago Miembro Nº: 27.979 Nacionalidad: Colegio/Liceo: Universidad: Sexo:	2 parte c? -------------------- Ex-Electrico Usach 2008 Mechón Injenieria 2009 Tengo Sed.

galois Ver Perfil del Miembro Ver los mensajes de este miembro	Nov 7 2010, 06:25 PM Publicado: #8
Maestro Matemático Grupo: Usuario FMAT Mensajes: 107 Registrado: 29-October 07 Desde: San Felipe-Santiago Miembro Nº: 11.941 Nacionalidad: Universidad: Sexo:	CITA(Crash! @ Nov 3 2010, 10:12 PM) 2 parte c? chuta era pa 1 c) lo voy a editar puse el 2 xq dcia los 2 puntos XD Mensaje modificado por galois el Nov 7 2010, 06:26 PM

Crash! Ver Perfil del Miembro Ver los mensajes de este miembro	Nov 7 2010, 08:14 PM Publicado: #9
Dios Matemático Supremo Grupo: Usuario FMAT Mensajes: 929 Registrado: 22-June 08 Desde: Santiago Miembro Nº: 27.979 Nacionalidad: Colegio/Liceo: Universidad: Sexo:	bueno, como seria eso del principio de identidad? que yo lo hice por cauchy riemmann -------------------- Ex-Electrico Usach 2008 Mechón Injenieria 2009 Tengo Sed.

galois Ver Perfil del Miembro Ver los mensajes de este miembro	Nov 9 2010, 06:52 PM Publicado: #10
Maestro Matemático Grupo: Usuario FMAT Mensajes: 107 Registrado: 29-October 07 Desde: San Felipe-Santiago Miembro Nº: 11.941 Nacionalidad: Universidad: Sexo:	f,g : G---> C analíticas f=g ssi { z en G tq f(z)=g(z)} tiene un punto de acumulación, en este caso la sucesión xn = 1/n te serviría para probar que la exponencial real, es la única función que cumple ciertas cosas a partir de las condiciones que tienes. Salu2

« Posterior · Cálculo Avanzado · Anterior »

Reply to this topic

Start new topic

1 usuario(s) está(n) leyendo esta discusión (1 invitado(s) y 0 usuario(s) anónimo(s))

0 miembro(s):

Modo de Ver: Estándar · Cambiar a: Lineal+ · Cambiar a: Outline

Suscribirse · Enviar por correo · Imprimir · Suscribirse a este foro

Versión Lo-Fi

Fecha y Hora actual: 4th April 2025 - 05:01 AM

Powered By IP.Board 2.2.1 © 2007 IPS, Inc.