I2 Variable Compleja - Foro fmat.cl

Foro fmat.cl > Programa Enseñanza Universitaria > Comunidades Universitarias > Universidad Católica > Variable Compleja

I2 Variable Compleja, 2S 2010

Opciones

Abu-Khalil Ver Perfil del Miembro Ver los mensajes de este miembro	Oct 18 2010, 07:44 PM Publicado: #1
Dios Matemático Supremo Grupo: Usuario FMAT Mensajes: 3.812 Registrado: 4-November 07 Desde: Santiago Miembro Nº: 12.213 Nacionalidad: Colegio/Liceo: Universidad: Sexo:	$TEX: \begin{center}MAT270I - Variable Compleja I\\<br />Interrogación 2 - Miércoles 18 de Octubre de 2010\end{center}<br />\begin{enumerate}<br />\item Sea $h$ analítica en una vecindad de $D=B(5,3)$, con $h(5)=i$ y tal que <br />\[\|h(z)\|>1,\quad \forall \|z-5\|=3.\]<br />Muestre que $h$ tiene un cero en $D$.<br />\item Supongamos que $f$ y $g$ son dos funciones analíticas en $D=B(0,1)$ y continuas en $\overline D$. Si además se tiene que $\Re f(z)=\Re g(z),\forall z\in\partial D$, pruebe que $f-g$ es una función constante.<br />\item Suponga que $f$ es una función entera tal que <br />\[\|f(z)\|\le 1+\|z\|^{\frac 32},\quad\forall z.\]<br />¿Qué puede concluir sobre $f$?<br />\item Para una función $f$ analítica en una vecindad de $D=B(0,1)$ se define la sucesión de funciones<br />\[f_n(z)=f(z^n),\quad n\ge 1,z\in D.\]<br />Pruebe que $\sum_nf_n$ es uniformemente convergente en compactos de $D$. Indicación: Use el Lema de Schwarz.<br />\end{enumerate}<br />$ --- A la 4) le falta la hipótesis de 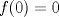$TEX: $f(0)=0$$ que no venía en el enunciado. -------------------- ~milopez $TEX: \[\mathfrak{L}=\int_{-\infty}^\infty e^{-289x^2}dx=\frac{\Gamma (\frac{1}{2})}{17}=\frac{\sqrt{\pi}}{17}\]$ $TEX: <br />\begin{equation}\begin{aligned}<br />dS_t&=\mu S_t dt+\sqrt{V_t}S_t dW^S_t\\<br />dV_t&=\kappa(\theta-V_t)dt+\sigma\sqrt{V_t} dW^V_t\\<br />\end{aligned}\end{equation}<br />$ $TEX: <br />$$\mathbb A^{\text U}_M(N)$$<br />$

Kaissa Ver Perfil del Miembro Ver los mensajes de este miembro	Oct 18 2010, 09:25 PM Publicado: #2
Dios Matemático Supremo Grupo: Usuario FMAT Mensajes: 9.897 Registrado: 6-April 08 Miembro Nº: 19.238 Nacionalidad: Colegio/Liceo: Sexo:	El problema 3 es la tipica "salvada pa los que hicieron la tarea", aunque en este caso para los que vieron la soloucion que entregó el "nuevo seco" de fmat ^^. -------------------- Este es un extracto de Qué es fmat by Kenshin. La pregunta para ti estimado(a) lector(a) es... ¿Qué haces tu para que ésto se cumpla?

Nicky Belane Ver Perfil del Miembro Ver los mensajes de este miembro	Apr 14 2015, 01:44 PM Publicado: #3
Principiante Matemático Grupo: Usuario FMAT Mensajes: 3 Registrado: 14-April 15 Miembro Nº: 136.973 Nacionalidad:	$TEX: 1) Supongamos que no alcance el 0 en D, se tiene por tanto que la funcion definida como $f=\frac {1}{h}$ es analitica, por tanto como consecuencia del teorema del modulo maximo tenemos que $\|f\|$ alcanza su maximo en el borde del disco, es decir $\|f(z)\|<1$ para todo $z$ en el disco, lo que contradice la hipotesis de que $h(5)=1$. Luego h tiene 0 en D.<br /><br />$ Mensaje modificado por Nicky Belane el Apr 18 2015, 10:01 AM -------------------- Nosotros somos los muertos

« Posterior · Variable Compleja · Anterior »

1 usuario(s) está(n) leyendo esta discusión (1 invitado(s) y 0 usuario(s) anónimo(s))

0 miembro(s):

Modo de Ver: Estándar · Cambiar a: Lineal+ · Cambiar a: Outline

Suscribirse · Enviar por correo · Imprimir · Suscribirse a este foro

Versión Lo-Fi

Fecha y Hora actual: 4th April 2025 - 05:02 AM