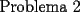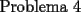Tarea Nº 2 - Foro fmat.cl

Portal Matemático

¿Qué es FMAT?

Foro fmat.cl > Programa de Enseñanza Media > Escuela de Verano > Verano Matemático > Intensivo Geometría

Reply to this topic

Start new topic

Tarea Nº 2, Cuadrilateros Ciclicos

Rurouni Kenshin Ver Perfil del Miembro Ver los mensajes de este miembro	Jan 13 2007, 06:00 PM Publicado: #1
Webmaster Grupo: Administrador Mensajes: 6.692 Registrado: 13-May 05 Desde: Santiago Centro Miembro Nº: 2 Nacionalidad: Sexo:	Y ya empezamos con "Cuadrilateros Ciclicos". Saludos Archivo(s) Adjunto(s) Tarea_Numero_2.doc ( 56.5k ) Número de descargas: 210 -------------------- Colegios/Liceos/Universidades en Fmat (Integrate!!!!) Videos PSU de Funciones (Y tú, ¿Aun estas aproblemado con Funciones?)

GlagosSA Ver Perfil del Miembro Ver los mensajes de este miembro	Jan 22 2007, 05:18 PM Publicado: #2
Dios Matemático Grupo: Usuario FMAT Mensajes: 380 Registrado: 22-April 06 Desde: Chillan, chile, sudamerica, el mundo Miembro Nº: 912 Nacionalidad: Colegio/Liceo: Universidad: Sexo:	$TEX: Problema 2$ $TEX: Nombremos $\angle TSR$ como $\alpha$, $\angle PST=\beta$, $\angle PQT=\gamma$ y $\angle TQR=\delta$. Para demostrar lo pedido basta demostrar que $\alpha +\delta=90$ y que $\beta + \gamma=90$, porque asi su suma = 180.\\<br />Se traslada $\beta$ al $\angle PAT$, gracias al ciclico PAST\\<br />Se traslada $\gamma$ al $\angle PBT$ gracias al ciclico QTPB\\<br />segun el $\triangle ABT$ tenemos que $\beta +\gamma=90$\\<br />Trasladamos $\delta$ al $\angle TCR$ gracias al ciclico QTRC\\<br />Trasladamos $\alpha$ al $\angle TDC$ gracias al ciclico TRDS\\<br />Segun el $\triangle TCD$, tenemos que $\alpha +\delta=90$\\<br />si sumamos las dos ecuaciones, obtendremos:\\<br />$\alpha +\beta +\gamma +\delta = 180$, demostrando asi lo pedido.$ Archivo(s) Adjunto(s) Tarea2p2.JPG ( 13.83k ) Número de descargas: 1 -------------------- Un dia aciago del año 212 a.C., durante la segunda querra punica, Arquimedes se encontraba contemplando algunos circulos que tenia dibujados sobre la arena. Un soldado romano trató de interrumpirlo. La reaccion del genio frente a la presencia del enemigo invasor, el lugar de ser miedo, fue indignacion por verse interrumpido en su trabajo intelectual.-"¡deje en paz a mis circulos!"- Unos minutos mas tarde, el maestro matematico de 75 años, muere atravesado por una espada romana. La altura de tu Vuelo dependera del tamaño de los Ideales que lleves por Alas.. El beso es la distancia mas corta entre Tú y Yo..

GlagosSA Ver Perfil del Miembro Ver los mensajes de este miembro	Jan 22 2007, 05:43 PM Publicado: #3
Dios Matemático Grupo: Usuario FMAT Mensajes: 380 Registrado: 22-April 06 Desde: Chillan, chile, sudamerica, el mundo Miembro Nº: 912 Nacionalidad: Colegio/Liceo: Universidad: Sexo:	$TEX: Problema 3$ $TEX: Como $\overline{PG}$ es reflejo de $\overline{DP}$, tenemos un isoceles con $\overline{EP}$ simetral, por lo tanto hay q demostrar que el angulo $\angle AEF=\angle GEP$ (porque serian opuestos por el vertice), pero como $\overline{EP}$ es simetral, $\angle GEP=\angle DEP$\\<br />Tenemos que BCEF es ciclico por los angulos rectos opuestos, por lo tanto $\angle BCF=\angle FEB=\alpha $, ademas, como $\angle ADC=90$, $\angle DMC=90-\alpha$, de ahi, $\angle AMF=90-\alpha$, luego $\angle BAD=\alpha$\\<br />Finalmente, sabemos que el ABDE es ciclico, por lo tanto $\angle AED=\angle BED=\alpha$, demostrando que $\angle AEF=\angle DEP$, probando lo pedido$ $TEX: Para otros gustos, bastaba con darse cuenta que $\triangle FED$ es ortico del $\triangle ABC$, con lo que sale directo que $\angle FEB=\angle BED$$ Archivo(s) Adjunto(s) Tarea2p3.JPG ( 20.58k ) Número de descargas: 0 -------------------- Un dia aciago del año 212 a.C., durante la segunda querra punica, Arquimedes se encontraba contemplando algunos circulos que tenia dibujados sobre la arena. Un soldado romano trató de interrumpirlo. La reaccion del genio frente a la presencia del enemigo invasor, el lugar de ser miedo, fue indignacion por verse interrumpido en su trabajo intelectual.-"¡deje en paz a mis circulos!"- Unos minutos mas tarde, el maestro matematico de 75 años, muere atravesado por una espada romana. La altura de tu Vuelo dependera del tamaño de los Ideales que lleves por Alas.. El beso es la distancia mas corta entre Tú y Yo..

GlagosSA Ver Perfil del Miembro Ver los mensajes de este miembro	Jan 22 2007, 06:14 PM Publicado: #4
Dios Matemático Grupo: Usuario FMAT Mensajes: 380 Registrado: 22-April 06 Desde: Chillan, chile, sudamerica, el mundo Miembro Nº: 912 Nacionalidad: Colegio/Liceo: Universidad: Sexo:	$TEX: Problema 4$ $TEX: Es necesario demostrar que $overline{BO}=\overline{CO}=\overline{AO}$, ya que ahi se demostraria que O es circuncentro al todos esos segmentos ser radios.\\<br />Sea $\angle DCE=\alpha$ y $\angle DBE=\beta$\\<br />Como $\triangle BDE$ es isoceles, $\angle BED=\angle EBD$. Del mismo modo, $\triangle CDE$ es isoceles, por lo que $\angle DCE=\angle CDE$\\<br />$\angle ADE=2\beta$ (por ser angulo exterior del vertice D en el $\triangle BED$\\<br />$\angle AED=2\alpha$ (por ser angulo exterior del vertice E en el $\triangle CED$\\<br />Como $\angle DAE=60$, segun $\triangle ADE$, $120=2\alpha +2\beta$, luego $\alpha +\beta=60$\\<br />Segun $\triangle DEO$, $180-(\alpha +\beta)=\angle DOE=120$, por lo tanto ADOE es ciclico (porque $\angle DAE + \angle DOE=180$)\\<br />Usando el ciclico, se traslada $\alpha$ en $\angle OAE$, por lo tanto $\triangle AOC$ es isoceles.\\<br />analogamente, se traslada $\beta$ en $\angle OAD$, por lo tanto $\triangle AOB$ es isoceles.\\<br />Demostrando que $\overline{BO}=\overline{CO}=\overline{AO}$$ Archivo(s) Adjunto(s) Tarea2p4.JPG ( 14.35k ) Número de descargas: 0 -------------------- Un dia aciago del año 212 a.C., durante la segunda querra punica, Arquimedes se encontraba contemplando algunos circulos que tenia dibujados sobre la arena. Un soldado romano trató de interrumpirlo. La reaccion del genio frente a la presencia del enemigo invasor, el lugar de ser miedo, fue indignacion por verse interrumpido en su trabajo intelectual.-"¡deje en paz a mis circulos!"- Unos minutos mas tarde, el maestro matematico de 75 años, muere atravesado por una espada romana. La altura de tu Vuelo dependera del tamaño de los Ideales que lleves por Alas.. El beso es la distancia mas corta entre Tú y Yo..

GlagosSA Ver Perfil del Miembro Ver los mensajes de este miembro	Sep 4 2007, 09:06 PM Publicado: #5
Dios Matemático Grupo: Usuario FMAT Mensajes: 380 Registrado: 22-April 06 Desde: Chillan, chile, sudamerica, el mundo Miembro Nº: 912 Nacionalidad: Colegio/Liceo: Universidad: Sexo:	$TEX: \noindent \textbf{Solucion Problema 1} Sabemos que $\angle CAB=\angle CBA=40$ y que $\angle RBA=20$, $\angle SAB=30$. Con esto, podemos decir, como es angulo externo del $\triangle ARB$, que $\angle CRB=60$, del mismo modo, $\angle CPA=120$, por ser angulo externo del $\triangle AKP$, por lo tanto, el cuadrilatero CPMR es ciclico.\\<br /> Por otra parte, $\overline{CK}$ es simetral del $\triangle ABC$, por lo que $\angle CBP=\angle CAS=10$, luego $\overline{CP}$ es bisectriz del $\angle CBR$, y como concurre con la bisectriz $\overline{CK}$, se sigue que $\overline{RP}$ es bisectriz del $\angle CRB$, entonces $\angle PRM=30$, pero CPMR es ciclico, en consiguiente $\angle MCK=30$\\<br /> Se concluye que $\angle ACM=20$ y $\angle BCM=80$$ Problema3.PNG ( 6.84k ) Número de descargas: 0 -------------------- Un dia aciago del año 212 a.C., durante la segunda querra punica, Arquimedes se encontraba contemplando algunos circulos que tenia dibujados sobre la arena. Un soldado romano trató de interrumpirlo. La reaccion del genio frente a la presencia del enemigo invasor, el lugar de ser miedo, fue indignacion por verse interrumpido en su trabajo intelectual.-"¡deje en paz a mis circulos!"- Unos minutos mas tarde, el maestro matematico de 75 años, muere atravesado por una espada romana. La altura de tu Vuelo dependera del tamaño de los Ideales que lleves por Alas.. El beso es la distancia mas corta entre Tú y Yo..

GlagosSA Ver Perfil del Miembro Ver los mensajes de este miembro	Sep 4 2007, 09:33 PM Publicado: #6
Dios Matemático Grupo: Usuario FMAT Mensajes: 380 Registrado: 22-April 06 Desde: Chillan, chile, sudamerica, el mundo Miembro Nº: 912 Nacionalidad: Colegio/Liceo: Universidad: Sexo:	$TEX: \noindent \textbf{Solucion Problema 5} Sea $\gamma =\angle BCF$, que usando los ciclicos ACDF y AEHF lo trasladamos a los angulos $\angle BAD$ y $\angle BEF$, respectivamente. \\<br />Sea $\angle LEB=\delta$. Notemos que $\overline{MH}=\overline{ME}$, puesto que M es punto medio de la hipotenusa del $\triangle AEH$, luego $\angle MHE=\delta$ y es inmediato que $\angle MHD=\delta$, pero BDHF es ciclico, y por tanto, $\angle BFD=\delta$, con lo que $\angle AFD=180-\delta$.\\<br />Veamos que $\angle BFD +\angle LEB=180$, luego ELFK es ciclico, que nos deja $\angle FLK=\gamma$.\\<br />Se sigue que $\overline{LK}//\overline{AD}$ y por tanto $\overline{LK}$ es perpendicular con $\overline{BC}$$ Ej5tarea2.PNG ( 10.49k ) Número de descargas: 0 -------------------- Un dia aciago del año 212 a.C., durante la segunda querra punica, Arquimedes se encontraba contemplando algunos circulos que tenia dibujados sobre la arena. Un soldado romano trató de interrumpirlo. La reaccion del genio frente a la presencia del enemigo invasor, el lugar de ser miedo, fue indignacion por verse interrumpido en su trabajo intelectual.-"¡deje en paz a mis circulos!"- Unos minutos mas tarde, el maestro matematico de 75 años, muere atravesado por una espada romana. La altura de tu Vuelo dependera del tamaño de los Ideales que lleves por Alas.. El beso es la distancia mas corta entre Tú y Yo..

« Posterior · Intensivo Geometría · Anterior »

Reply to this topic

Start new topic

1 usuario(s) está(n) leyendo esta discusión (1 invitado(s) y 0 usuario(s) anónimo(s))

0 miembro(s):

Modo de Ver: Estándar · Cambiar a: Lineal+ · Cambiar a: Outline

Suscribirse · Enviar por correo · Imprimir · Suscribirse a este foro

Versión Lo-Fi

Fecha y Hora actual: 4th April 2025 - 04:59 AM

Powered By IP.Board 2.2.1 © 2007 IPS, Inc.