 P016, Resuelto por Caro |
|
|
|
|
|
|
Foro fmat.cl > Sector Preparación Olimpiadas > Competencias y Olimpiadas > El Gran Desafío > El Gran Desafío VI > Problemas Resueltos  |
 Jan 10 2007, 11:03 PM
Publicado:
#1
|
|
 Dios Matemático Supremo  Grupo: Colaborador Silver Mensajes: 725 Registrado: 17-July 05 Desde: Puente Alto-Santiago Miembro Nº: 148 Nacionalidad:  Universidad:  Sexo:   |
 ![TEX: <br />\[<br />\begin{gathered}<br /> \text{Si el per\'imetro de un rombo es de 52 cm}\text{. y una de sus diagonales mide} \hfill \\<br /> \text{24 cm}.,\text{ Cu\'al es su \'area?} \hfill \\ <br />\end{gathered} <br />\]<br />](./tex/1168488208.gif)
-------------------- "Resolver un problema es una meta específica de la inteligencia e inteligencia es el don específico de los seres humanos: Resolver un problema es la actividad humana por excelencia"
  |
 |
 
|
 Jan 13 2007, 08:45 PM
Publicado:
#2
|
|
 Maestro Matemático  Grupo: Usuario FMAT Mensajes: 106 Registrado: 14-October 06 Desde: Valdivia Miembro Nº: 2.493 Nacionalidad: Universidad:  Sexo:  |
El perímetro mide 52cm, entonces cada lado mide 52:4=13cm.
Las diagonales dividen al rombo en 4 triángulos rectángulos, cada uno de catetos equivalentes a la mitad de cada diagonal e hipotenusas formadas por los lados del rombo (las diagonales se intersectan perpendicularmente). Si una diagonal mide 24cm, cada uno de estos triangulitos descritos anteriormente posee una hipotenusa de 13cm y un cateto de 12 cm (la mitad de la diagonal); el otro cateto mide, por el trío pitagórico, 5cm. El área del rombo, que es lo que nos piden, puede ser vista como la suma de las áreas de todos los triángulos, o sea, 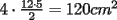 Aunque yo la veo más bien como un rectángulo de lados 10 y 12, si acomodamos los rectángulos para formarlo. Sorry por no poner dibujo, pero me dio flojera hacerlo con el paint y subirlo... a propósito, necesito conseguirme un programa 
--------------------   ^^!!! |
|
|
|
|
Jan 14 2007, 01:23 PM
Publicado:
#3
|
|
|
Dios Matemático Supremo Grupo: Colaborador Silver Mensajes: 725 Registrado: 17-July 05 Desde: Puente Alto-Santiago Miembro Nº: 148 Nacionalidad: Universidad: Sexo: |
Respuesta correcta!
 pd: un buen programa para hacer dibujos puede ser el Cabri Geomete II  - - - - Rayos :S se me traslado de inmediato :S Por favor, Administrador, Mover a Problemas Resueltos de El Gran Desafio 6 
Mensaje modificado por dex el Jan 14 2007, 01:25 PM -------------------- "Resolver un problema es una meta específica de la inteligencia e inteligencia es el don específico de los seres humanos: Resolver un problema es la actividad humana por excelencia"
|
|
|
|
|
1 usuario(s) está(n) leyendo esta discusión (1 invitado(s) y 0 usuario(s) anónimo(s))
0 miembro(s):
| Versión Lo-Fi | Fecha y Hora actual: 23rd November 2024 - 07:48 PM |
