|
|
|
|
|
|
|
  |
 Sep 8 2005, 11:02 AM Sep 8 2005, 11:02 AM
Publicado:
#1
|
|
|
Webmaster Grupo: Administrador Mensajes: 6.692 Registrado: 13-May 05 Desde: Santiago Centro Miembro Nº: 2 Nacionalidad:  Sexo:  |
Sean X, Y, Z puntos de los lados BC, CA y AB respectivamente de un triángulo ABC. Los segmentos AX, BY y CZ se denominan cevianas, término que procede del matemático italiano Giovanni Ceva (1647-1734).
Aquí podemos ver tres cevianas de un triángulo cumpliendo el teorema de Ceva.  El teorema de Ceva afirma: Si las tres cevianas AX, BY y CZ son concurrentes, entonces  Demostración del teorema La siguiente demostración se basa en que las áreas de los triángulos con alturas iguales son proporcionales a las bases de los triángulos. Supongamos que las tres cevianas AX, BY y CX se cortan en un punto P.  Entonces  De la misma forma, se obtiene que  Multiplicando,  El recíproco del teorema de Ceva es también cierto. Es decir, se cumple que Supongamos que las tres cevianas AX, BY y CZ cumplen  Entonces las tres cevianas son concurrentes. La demostracion del reciproco queda propuesta para nuestros usuarios. PD:La verdad es que quienes conocen bien este teorema saben que los puntos X,Y,Z no necesariamente tienen que estar adentro del triangulo...seria interesante generar una discusion al respecto. -------------------- Colegios/Liceos/Universidades en Fmat (Integrate!!!!)
Videos PSU de Funciones (Y tú, ¿Aun estas aproblemado con Funciones?)   |
|
|
|
 Sep 17 2005, 10:58 PM Sep 17 2005, 10:58 PM
Publicado:
#2
|
|
|
Webmaster Grupo: Administrador Mensajes: 6.692 Registrado: 13-May 05 Desde: Santiago Centro Miembro Nº: 2 Nacionalidad:  Sexo:  |
Aca una Demostracion Alternativa del Teorema de Ceva usando el Teorema de Menelao
Enunciado y Demostracion del Teorema de Ceva Espero lo disfruten tanto como yo Necesitan de Flash Player para poder verlo...asi que si no lo tienen...aca pueden descargarlo Flash Player -------------------- Colegios/Liceos/Universidades en Fmat (Integrate!!!!)
Videos PSU de Funciones (Y tú, ¿Aun estas aproblemado con Funciones?)   |
|
|
|
 Mar 1 2006, 05:43 PM Mar 1 2006, 05:43 PM
Publicado:
#3
|
|
 Staff Fmat Grupo: Moderador Mensajes: 1.185 Registrado: 29-October 05 Desde: Santiago, Chile Miembro Nº: 352 Nacionalidad:  Colegio/Liceo:  Universidad:  Sexo:  |
CITA(Kenshin @ Sep 8 2005, 12:02 PM) El recíproco del teorema de Ceva es también cierto. Es decir, se cumple que Supongamos que las tres cevianas AX, BY y CZ cumplen  screen.width*0.6) {this.resized=true; this.width=screen.width*0.4; this.alt='Pincha Aqui para ver esta imagen en su tamaño original';}" onmouseover="if(this.resized) this.style.cursor='hand';" onclick="if(this.resized) {window.open('http://img317.imageshack.us/img317/4056/g71ra.png');}" /> screen.width*0.6) {this.resized=true; this.width=screen.width*0.4; this.alt='Pincha Aqui para ver esta imagen en su tamaño original';}" onmouseover="if(this.resized) this.style.cursor='hand';" onclick="if(this.resized) {window.open('http://img317.imageshack.us/img317/4056/g71ra.png');}" />Entonces las tres cevianas son concurrentes. La demostracion del reciproco queda propuesta para nuestros usuarios. Demostración:  screen.width*0.6) {this.resized=true; this.width=screen.width*0.4; this.alt='Pincha Aqui para ver esta imagen en su tamaño original';}" onmouseover="if(this.resized) this.style.cursor='hand';" onclick="if(this.resized) {window.open('http://img344.imageshack.us/img344/5863/rceva4lp.png');}" /> screen.width*0.6) {this.resized=true; this.width=screen.width*0.4; this.alt='Pincha Aqui para ver esta imagen en su tamaño original';}" onmouseover="if(this.resized) this.style.cursor='hand';" onclick="if(this.resized) {window.open('http://img344.imageshack.us/img344/5863/rceva4lp.png');}" />Para probar esto, supongamos que las cevianas 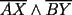 concurren en concurren en 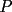 , como en el teorema de Ceva, y que una tercera ceviana que pasa por , como en el teorema de Ceva, y que una tercera ceviana que pasa por 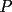 es es 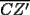 . Luego, por el teorema de Ceva: . Luego, por el teorema de Ceva: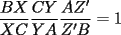 Pero estamos asumiendo (enunciado): 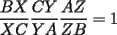 Entonces: 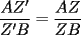 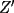 coincide con coincide con 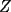 , entonces hemos probado que , entonces hemos probado que 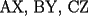 son concurrentes. son concurrentes.Saludos -------------------- "He looks rather ill, but he looks all over the genius he was" (G. H. Hardy)
"A mathematician is a device for turning coffee into theorems" (Paul Erdös) |
|
|
|
 Mar 1 2006, 06:06 PM Mar 1 2006, 06:06 PM
Publicado:
#4
|
|
|
Webmaster Grupo: Administrador Mensajes: 6.692 Registrado: 13-May 05 Desde: Santiago Centro Miembro Nº: 2 Nacionalidad:  Sexo:  |
CITA 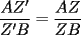 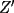 coincide con coincide con 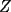 , entonces hemos probado que , entonces hemos probado que 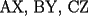 son concurrentes. son concurrentes.Me gustaria ver una demostracion de esto ultimo... Todo lo demas es super claro, pero ese paso es uno que el coxeter no justifica, y seria bueno tener algun fundamento... Saludos -------------------- Colegios/Liceos/Universidades en Fmat (Integrate!!!!)
Videos PSU de Funciones (Y tú, ¿Aun estas aproblemado con Funciones?)   |
|
|
|
 Mar 1 2006, 06:33 PM Mar 1 2006, 06:33 PM
Publicado:
#5
|
|
 Staff Fmat Grupo: Moderador Mensajes: 1.185 Registrado: 29-October 05 Desde: Santiago, Chile Miembro Nº: 352 Nacionalidad:  Colegio/Liceo:  Universidad:  Sexo:  |
CITA(Kenshin @ Mar 1 2006, 07:06 PM) Me gustaria ver una demostracion de esto ultimo... Todo lo demas es super claro, pero ese paso es uno que el coxeter no justifica, y seria bueno tener algun fundamento... Saludos Bueno, primero: 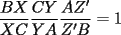 y: y: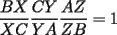 Entonces: 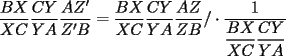 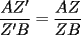 Lo segundo: Ya que las cevianas 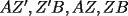 concurren en concurren en  , se concluye que , se concluye que 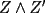 son el mismo punto. son el mismo punto.Saludos y ojalá esté claro. -------------------- "He looks rather ill, but he looks all over the genius he was" (G. H. Hardy)
"A mathematician is a device for turning coffee into theorems" (Paul Erdös) |
|
|
|
 Mar 1 2006, 07:55 PM Mar 1 2006, 07:55 PM
Publicado:
#6
|
|
|
Webmaster Grupo: Administrador Mensajes: 6.692 Registrado: 13-May 05 Desde: Santiago Centro Miembro Nº: 2 Nacionalidad:  Sexo:  |
CITA(Killua @ Mar 1 2006, 08:33 PM) Bueno, primero: 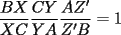 y: y: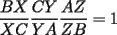 Entonces: 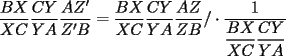 Se concluye lo primero. Lo segundo: Ya que las cevianas 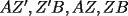 concurren en concurren en 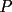 , se concluye que , se concluye que 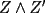 son el mismo punto. son el mismo punto.Saludos y ojalá esté claro. Ahora con mayor razon, puedo decirte que no es correcto, por los siguiente motivos. 1) ¿Como llegaste a la conclusion que ambas concurrian en el mismo punto P? 2) ¿Entonces de que sirvio probar lo primero? Saludos -------------------- Colegios/Liceos/Universidades en Fmat (Integrate!!!!)
Videos PSU de Funciones (Y tú, ¿Aun estas aproblemado con Funciones?)   |
|
|
|
 Mar 1 2006, 08:42 PM Mar 1 2006, 08:42 PM
Publicado:
#7
|
|
 Staff Fmat Grupo: Moderador Mensajes: 1.185 Registrado: 29-October 05 Desde: Santiago, Chile Miembro Nº: 352 Nacionalidad:  Colegio/Liceo:  Universidad:  Sexo:  |
CITA(Kenshin @ Mar 1 2006, 08:55 PM) Ahora con mayor razon, puedo decirte que no es correcto, por los siguiente motivos. 1) ¿Como llegaste a la conclusion que ambas concurrian en el mismo punto P? 2) ¿Entonces de que sirvio probar lo primero? Saludos Bueno, para concluir que 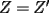 , tenemos que probar que , tenemos que probar que 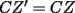 Notemos que 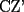 pasa por pasa por 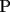 , o sea , o sea  es la prolongación del es la prolongación del 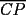 . Del mismo modo . Del mismo modo 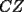 es la prolongación de es la prolongación de 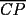 . Y tenemos que uno de los postulados de Euclides dice que por dos puntos pasa sólo una recta. Se concluye que . Y tenemos que uno de los postulados de Euclides dice que por dos puntos pasa sólo una recta. Se concluye que 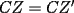 , y los puntos , y los puntos 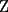 y y 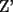 son el mismo (al pertenecer a la misma recta) son el mismo (al pertenecer a la misma recta)Saludos -------------------- "He looks rather ill, but he looks all over the genius he was" (G. H. Hardy)
"A mathematician is a device for turning coffee into theorems" (Paul Erdös) |
|
|
|
 Mar 1 2006, 08:55 PM Mar 1 2006, 08:55 PM
Publicado:
#8
|
|
 Staff Fmat Grupo: Moderador Mensajes: 1.185 Registrado: 29-October 05 Desde: Santiago, Chile Miembro Nº: 352 Nacionalidad:  Colegio/Liceo:  Universidad:  Sexo:  |
Otra demostración de que
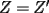 , a partir de lo primero: , a partir de lo primero:Por la propiedad 3 de Relaciones entre áreas y bases, tenemos que: 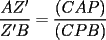 Y: 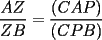 Luego, 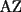 y y 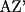 , , 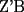 y y 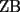 son el mismo segmento y son el mismo segmento y 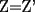
-------------------- "He looks rather ill, but he looks all over the genius he was" (G. H. Hardy)
"A mathematician is a device for turning coffee into theorems" (Paul Erdös) |
|
|
|
 Mar 1 2006, 09:00 PM Mar 1 2006, 09:00 PM
Publicado:
#9
|
|
|
Webmaster Grupo: Administrador Mensajes: 6.692 Registrado: 13-May 05 Desde: Santiago Centro Miembro Nº: 2 Nacionalidad:  Sexo:  |
CITA(Killua @ Mar 1 2006, 10:42 PM) Bueno, para concluir que 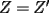 , tenemos que probar que , tenemos que probar que 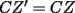 Notemos que 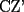 pasa por pasa por 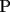 , o sea , o sea 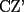 es la prolongación del es la prolongación del 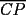 . Del mismo modo . Del mismo modo 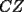 es la prolongación de es la prolongación de 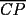 . Y tenemos que uno de los postulados de Euclides dice que por dos puntos pasa sólo una recta. Se concluye que . Y tenemos que uno de los postulados de Euclides dice que por dos puntos pasa sólo una recta. Se concluye que 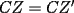 , y los puntos , y los puntos 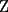 y y 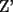 son el mismo (al pertenecer a la misma recta) son el mismo (al pertenecer a la misma recta)Saludos Creo que la confusion aun continua..asi que tendre que ser mas explicito... Fijate bien en lo que vamos a probar(esto es importante, pues tu tienes un dato...que no has usado...) Esa propiedad te permitio implicar que 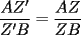 Esto es un detalle super importante, pues hasta ahora en ningun momento has usado ese dato, y por ende sigo preguintandome...¿para que probaste eso entonces? Pero lo mas importante, tienes confusion en tu construccion, pues en ningun caso tu sabes que 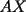 , , 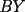 y y 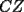 concurran, y mucho menos tienes certeza que concurran, y mucho menos tienes certeza que 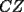 sea la prolongacion de sea la prolongacion de 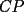 . De hecho si eso fuera cierto, entonces simplemente nos olvidamos de todo lo hecho durante la demostracion, y seria evidente que . De hecho si eso fuera cierto, entonces simplemente nos olvidamos de todo lo hecho durante la demostracion, y seria evidente que 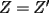 , y entonces estariamos listos.... , y entonces estariamos listos.... Creo que antes de postear de nuevo, reflexiona muy bien lo que estas tratando de demostrar, y que figura es valida en tu demostracion(dado que el teorema de ceva tiene una doble implicancia, creo que para la implicancia de vuelta, estas mirando la figura de ida...) Bueno, eso..saludos PD: A seguir pensando... -------------------- Colegios/Liceos/Universidades en Fmat (Integrate!!!!)
Videos PSU de Funciones (Y tú, ¿Aun estas aproblemado con Funciones?)   |
|
|
|
 Mar 1 2006, 09:02 PM Mar 1 2006, 09:02 PM
Publicado:
#10
|
|
|
Webmaster Grupo: Administrador Mensajes: 6.692 Registrado: 13-May 05 Desde: Santiago Centro Miembro Nº: 2 Nacionalidad:  Sexo:  |
CITA(Killua @ Mar 1 2006, 10:55 PM) Otra demostración de que 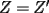 , a partir de lo primero: , a partir de lo primero:Por la propiedad 3 de Relaciones entre áreas y bases, tenemos que: 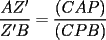 Y: 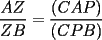 Luego, 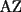 y y 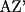 , , 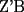 y y 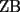 son el mismo segmento y son el mismo segmento y 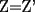 Seguimos con el mismo error.... Insisto, tienes que comprender que para la vuelta, tu no tienes la certeza de la concurrencia, y tu quieres probar que la concurrencia efectivamente se da... Saludos -------------------- Colegios/Liceos/Universidades en Fmat (Integrate!!!!)
Videos PSU de Funciones (Y tú, ¿Aun estas aproblemado con Funciones?)   |
|
|
|
  |
1 usuario(s) está(n) leyendo esta discusión (1 invitado(s) y 0 usuario(s) anónimo(s))
0 miembro(s):
| Versión Lo-Fi | Fecha y Hora actual: 18th April 2025 - 06:02 PM |










