|
|
|
|
|
|
|
  |
 Sep 5 2010, 09:21 AM Sep 5 2010, 09:21 AM
Publicado:
#1
|
|
 Dios Matemático Supremo Grupo: Administrador Mensajes: 2.706 Registrado: 13-May 05 Desde: Santiago de Chile Miembro Nº: 10 Nacionalidad:  Colegio/Liceo:  Sexo:  |
VIII CAMPEONATO ESCOLAR DE MATEMÁTICA - CMAT Fecha 5: Sábado 4 de Septiembre de 2010 Cuarto Nivel Individual Problema 1 Consideremos una función 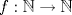 tal que: tal que:
Aclaración: En este problema considere 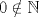 Problema 2 Considere un triángulo 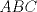 con alturas con alturas 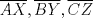 e inscrito en una circunferencia e inscrito en una circunferencia 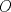 . Sean . Sean 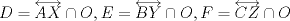 . Si . Si 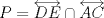 y y 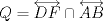 , demueste que B,C, P y Q son concíclicos. , demueste que B,C, P y Q son concíclicos.
-------------------- |
|
|
|
  |
1 usuario(s) está(n) leyendo esta discusión (1 invitado(s) y 0 usuario(s) anónimo(s))
0 miembro(s):
| Versión Lo-Fi | Fecha y Hora actual: 17th October 2025 - 12:23 AM |





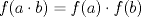 si el máximo divisor común de a y b es 1
si el máximo divisor común de a y b es 1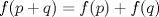 si p y q son primos
si p y q son primos

