|
|
|
|
|
|
|
  |
 Aug 29 2010, 12:50 PM Aug 29 2010, 12:50 PM
Publicado:
#21
|
|
 Dios Matemático Supremo Grupo: Usuario FMAT Mensajes: 1.564 Registrado: 12-November 07 Desde: La Union, XIV Region de los Rios Miembro Nº: 12.607 Nacionalidad:  Colegio/Liceo:  Universidad:  Sexo:  |
si hay "masacre" es bueno?? a mi el P2 me dió el doble u.u xD Si hay masacre, significa que tienes mas chance de clasificar a la final (dependiendo de como te haya ido). El asunto es que a cada sede regional les dicen cuantos deben ir por sede (por ejemplo, dicen: "Deben ir 5 de la Región de los Ríos") y entonces escojen a los mejores puntajes de las sedes. Eso según me contó mi profe. La idea de esto es hacer que vayan representantes de cada región y no vayan solamente finalistas de la metropolitana por ejemplo. Respecto al Problema 2, Kenshin dijo varios post atrás que tal vez hay pueda ser el doble de lo que dije. Entonces, si lo explicas bien puedes rescatar valiosisimos puntos (en total cada problema tiene 10 puntos) o bien puedes rescatar los 10. Pero no tengo muy claro si es 296 o 592. Voto por 592, pero por lo siguiente. Recorrer de arriba a abajo es lo mismo (segun mi opinion) pero añado lo que es recorrer de derecha a izquierda. Tratándose de combinatoria, yo no me confío mucho. Y lo de la matriz, no ocupé naaada avanzado. Solamente la usé como notación, y lo único que hize fue sumar en diagonal. Solo era para ser mas ordenado con las cuentas numericas. Saludos y exito a todos. -------------------- Ricardo Vargas Obando
Ex-alumno Deutsche Schule La Unión (Generación 2010, de los 150 años). Novato de Licenciatura en Matemática/Estadística, en la Pontificia Universidad Católica de Chile.  Grupo de facebook de Novatos Matemática y Estadística PUC 2011 Currículum Olímpico:
|
|
|
|
 Aug 29 2010, 12:51 PM Aug 29 2010, 12:51 PM
Publicado:
#22
|
|
|
Dios Matemático Supremo Grupo: Usuario FMAT Mensajes: 2.847 Registrado: 3-October 09 Miembro Nº: 59.760 Nacionalidad:  Colegio/Liceo:  Universidad:  Sexo:  |
es la primera que asistía a esta olimpiada, y la encontré muy difícil, el viernes fuimos a la del san mateo y el profe nos dijo "oie el sábado hay otra olimpiada de la somachi" pero igual estoy conforme con lo que hice. creo que tengo 2 buenas y la que se hacia por inducción la había hecho así y después me arrepentí y le mande chamullo
|
|
|
|
 Aug 29 2010, 01:01 PM Aug 29 2010, 01:01 PM
Publicado:
#23
|
|
 Doctor en Matemáticas Grupo: Usuario FMAT Mensajes: 143 Registrado: 6-February 08 Desde: desde aquí Miembro Nº: 15.300 Nacionalidad:  Colegio/Liceo:  Sexo:  |
Yo también creo que fue masacre, sabes kenshin, viendo tu solucion del p6 me di cuenta que estaba muy cerca, me faltó concluir lo de la media aritmetica. Bueno será estuve a medio camino u.u como vi que no puede hacer mucho me tiré a analitica y ahí morí.
emm en el p2 yo consideré ambos sentidos, aun así no me salío xDD FAIL y sería tengo bueno el 1, 3, 4 (incluyendo la demostración trucha alfinal que me mató de la risa xD) y el 5 el p6 tendría la mitad... igual creo que me fue bien, esperemos que sea suficiente y no me descuenten puntos por algun error trucho. -------------------- |Ente Inmiscible|  |
|
|
|
 Aug 29 2010, 01:12 PM Aug 29 2010, 01:12 PM
Publicado:
#24
|
|
|
Dios Matemático Supremo Grupo: Usuario FMAT Mensajes: 2.818 Registrado: 3-October 09 Miembro Nº: 59.773 Nacionalidad:  Colegio/Liceo:  Universidad:  Sexo:  |
No entendí la super solución de makmat
Se ve interesante eso de "sin perder generalidad"... soluciones tan marcianas, me bajan el autoestima -------------------- Me voy, me jui.
|
|
|
|
 Aug 29 2010, 01:13 PM Aug 29 2010, 01:13 PM
Publicado:
#25
|
|
|
Principiante Matemático Destacado Grupo: Usuario FMAT Mensajes: 29 Registrado: 24-September 08 Desde: Rancagua!! Miembro Nº: 34.885 Nacionalidad:  Colegio/Liceo:  Universidad:  Sexo:  |
Si hay masacre, significa que tienes mas chance de clasificar a la final (dependiendo de como te haya ido). El asunto es que a cada sede regional les dicen cuantos deben ir por sede (por ejemplo, dicen: "Deben ir 5 de la Región de los Ríos") y entonces escojen a los mejores puntajes de las sedes. Eso según me contó mi profe. La idea de esto es hacer que vayan representantes de cada región y no vayan solamente finalistas de la metropolitana por ejemplo. Respecto al Problema 2, Kenshin dijo varios post atrás que tal vez hay pueda ser el doble de lo que dije. Entonces, si lo explicas bien puedes rescatar valiosisimos puntos (en total cada problema tiene 10 puntos) o bien puedes rescatar los 10. Pero no tengo muy claro si es 296 o 592. Voto por 592, pero por lo siguiente. Recorrer de arriba a abajo es lo mismo (segun mi opinion) pero añado lo que es recorrer de derecha a izquierda. Tratándose de combinatoria, yo no me confío mucho. Y lo de la matriz, no ocupé naaada avanzado. Solamente la usé como notación, y lo único que hize fue sumar en diagonal. Solo era para ser mas ordenado con las cuentas numericas. Saludos y exito a todos. weeena entonces, en volá si se puede clasificarr xD |
|
|
|
 Aug 29 2010, 01:21 PM Aug 29 2010, 01:21 PM
Publicado:
#26
|
|
 Dios Matemático Supremo Grupo: Usuario FMAT Mensajes: 858 Registrado: 20-August 09 Desde: In my House Miembro Nº: 57.323 Nacionalidad:  Colegio/Liceo:  Universidad:  Sexo:  |
Una forma sin piedad de matar el P1: Saludos. PD: Era por si querian una solución corta. xD jajaja muirhead en la nacional xd 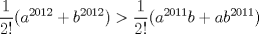 y listo xdd y listo xddno pense usarlo xdd, me dedique a hacer el p2 y no me salio nada solo me salieron el 1,3 y 4 D: el 5 me failie en el par y el 6 no escribi nada ojala que pueda clasificar saludos |
|
|
|
 Aug 29 2010, 01:31 PM Aug 29 2010, 01:31 PM
Publicado:
#27
|
|
|
Dios Matemático Supremo Grupo: Usuario FMAT Mensajes: 2.818 Registrado: 3-October 09 Miembro Nº: 59.773 Nacionalidad:  Colegio/Liceo:  Universidad:  Sexo:  |
Una forma sin piedad de matar el P1: Saludos. PD: Era por si querian una solución corta. xD http://www.worldlingo.com/ma/enwiki/es/Mui...39;s_inequality Cuando decía "muirhead" crei que era jugoseo... Google never lies -------------------- Me voy, me jui.
|
|
|
|
 Aug 29 2010, 02:33 PM Aug 29 2010, 02:33 PM
Publicado:
#28
|
|
 Maestro Matemático Grupo: Usuario FMAT Mensajes: 113 Registrado: 16-April 10 Desde: Arriving somewhere, but not here Miembro Nº: 68.879 Nacionalidad:  Colegio/Liceo:  Universidad:  Sexo:  |
Asumamos, sin perdida de generalidad, que 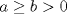 . .Luego, 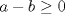 . Y además, . Y además, 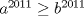 por lo que por lo que 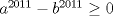 . .Como estamos hablando de numeros positivos, podemos multiplicar estas 2 desigualdades miembro a miembro, sin alterar el sentido de éstas: 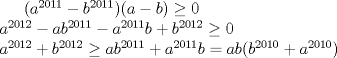 Luego, como a y b son positivos, entonces la suma de sus potencias 2010-esimas tambien lo será...podemos dividir la desigualdad por esta suma, sin alterar el sentido de la desigualdad... 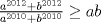 Demostrando lo pedido. =D Ojalá esté bien. Demostrando lo pedido. =D Ojalá esté bien.Hice lo mismo, pero partiendo desde el enunciado, multipliqué por el denominador, resté y deje la inecuación con respecto al 0, factorizé y tome los 3 casos posibles (a=b, a>b, a<b) Quedé contento, ya que como todo un novato en las olimpiadas, mi participación fué muy buena Saludos a todos --------------------     have fun Ing. Civil Eléctrica, Campus San Joaquín |
|
|
|
 Aug 29 2010, 02:41 PM Aug 29 2010, 02:41 PM
Publicado:
#29
|
|
|
Webmaster Grupo: Administrador Mensajes: 6.692 Registrado: 13-May 05 Desde: Santiago Centro Miembro Nº: 2 Nacionalidad:  Sexo:  |
Para el P5, voy a dar algunas lineas de ideas para que lo puedan trabajar. 1) Descartar las posibilidades m=1 y n=1. 2) Como 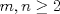 , entonces , entonces 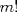 y y 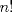 son pares, por lo cual lo es también son pares, por lo cual lo es también 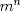 . Finalmente, . Finalmente,  debe ser par. debe ser par.3) Si probamos con 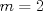 , notaremos que , notaremos que 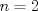 y y 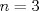 funcionan. Por un argumento posterior (item 6), descartaremos el caso funcionan. Por un argumento posterior (item 6), descartaremos el caso 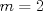 , , 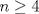 . .4*) Acá esta el punto clave, y se refiere a la máxima potencia de 2 que divide a un factorial. Ese número es posible obtenerlo usando la "Fórmula de Legendre" Fórmula de Legendre http://www.artofproblemsolving.com/Wiki/in...e's_Formula. En este caso, nos interesan 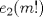 y y 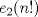 . .En realidad lo que nos interesa de la Fórmula de Legendre es que 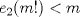 (verifique esto acotando superiormente la fórmula de Legendre). (verifique esto acotando superiormente la fórmula de Legendre).Por ejemplo 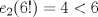 , , 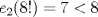 , etc... , etc...5) Luego intente concluir que "la mayor potencia de 2" que divide a m y n es la misma, pues de otro modo podría llegar a una contradicción del estilo par+impar=par (el [4*] es clave en el sentido que podría eventualmente quedar par+impar=impar lo cual no generaría contradicción, pero en [4*] la desigualdad estricta lo impide). 6) Finalmente, hay solo 2 casos, que 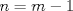 y y 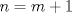 los cuales se pueden trabajar independientemente (descartando ambas opciones a traves de desigualdades probables via Inducción para los cuales se pueden trabajar independientemente (descartando ambas opciones a traves de desigualdades probables via Inducción para  [recordar que m es par], analizando aparte si es necesario el caso m=4). [recordar que m es par], analizando aparte si es necesario el caso m=4).Por supuesto, aspiro a que esta solución sea acortable Saludos PD: A modo de ejemplo, para descartar que 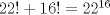 (sin calcular los factoriales, claro está), nos fijamos en que 22! es divisible "a lo mas" por (sin calcular los factoriales, claro está), nos fijamos en que 22! es divisible "a lo mas" por 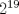 (o sea, que (o sea, que 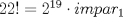 ) y 16! es divisible "a lo mas" por ) y 16! es divisible "a lo mas" por 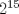 (o sea, (o sea, 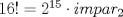 ). ).Luego, si se cumpliera que 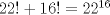 , entonces , entonces  . . Si dividimos todo por 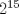 , nos queda que par+impar=par (contradicción!!). , nos queda que par+impar=par (contradicción!!).Lo que me preocupaba es que pasaba si en vez de esta situación, quedaba algo como 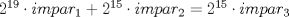 , pero eso no es posible por la desigualdad estricta del [4*]. , pero eso no es posible por la desigualdad estricta del [4*].PD: Por supuesto que para descartar que 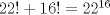 se podría decir que el lado izquierdo es divisible por 3, y el derecho no, pero ese argumento es muy "particular" para el 22. se podría decir que el lado izquierdo es divisible por 3, y el derecho no, pero ese argumento es muy "particular" para el 22.-------------------- Colegios/Liceos/Universidades en Fmat (Integrate!!!!)
Videos PSU de Funciones (Y tú, ¿Aun estas aproblemado con Funciones?)   |
|
|
|
 Aug 29 2010, 08:27 PM Aug 29 2010, 08:27 PM
Publicado:
#30
|
|
 Maestro Matemático Grupo: Usuario FMAT Mensajes: 79 Registrado: 27-April 10 Desde: Talagante Miembro Nº: 69.788 Nacionalidad:  Colegio/Liceo:  Universidad:  Sexo:  |
nosotros fuimos por primera vez a la olimpiadas, luego de que sorpresa nos avisaran una semana antes, pero fue una gran experiencia, nuestro profe de verdad se las jugo y espero que el colegio lo valore
si no se pudo ahora será para el prox. año saludos --------------------    |
|
|
|
  |
2 usuario(s) está(n) leyendo esta discusión (2 invitado(s) y 0 usuario(s) anónimo(s))
0 miembro(s):
| Versión Lo-Fi | Fecha y Hora actual: 2nd April 2025 - 02:30 AM |









