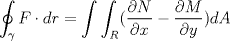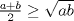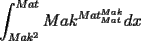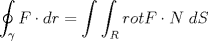|
|
|
|
|
|
|
  |
 Aug 28 2010, 08:31 PM Aug 28 2010, 08:31 PM
Publicado:
#1
|
|
 Dios Matemático Supremo Grupo: Usuario FMAT Mensajes: 858 Registrado: 20-August 09 Desde: In my House Miembro Nº: 57.323 Nacionalidad:  Colegio/Liceo:  Universidad:  Sexo:  |
22ª OLIMPIADA NACIONAL DE MATEMÁTICAS Prueba de Clasificación, Nivel Mayor Primera Prueba Problema 1: Pruebe que si 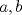 son números reales positivos entonces son números reales positivos entonces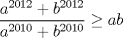 Problema 2: Considere un tablero de ajedrez de 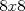 . Se define una trayectoria Alba a cualquier movimiento que contenga . Se define una trayectoria Alba a cualquier movimiento que contenga 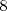 casillas blancas, una por fila, que se tocan en un vértice. Determine todas las posibles trayectorias albas que se pueden construir en el tablero. casillas blancas, una por fila, que se tocan en un vértice. Determine todas las posibles trayectorias albas que se pueden construir en el tablero.Problema 3: Encuentre todos los números primos 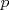 tales que tales que 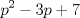 y y 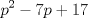 son también primos son también primosSegunda Prueba Problema 4: Pruebe que para todo entero  , los números de la forma , los números de la forma 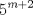 se pueden escribir como suma de tres cuadrados de números enteros. se pueden escribir como suma de tres cuadrados de números enteros.Problema 5: Determine todos los pares 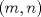 de números enteros positivos que satisfagan la ecuación de números enteros positivos que satisfagan la ecuación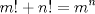 Problema 6: En el interior de un triángulo equilátero de lado 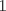 se encuentran dos circunferencias tangentes entre si y cada una de estas tangentes al menos a dos de los lados del triángulo. Demostrar que la suma de los radios de estas circunferencias es mayor o igual a se encuentran dos circunferencias tangentes entre si y cada una de estas tangentes al menos a dos de los lados del triángulo. Demostrar que la suma de los radios de estas circunferencias es mayor o igual a 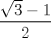 . ¿En qué casos se alcanza la igualdad? . ¿En qué casos se alcanza la igualdad?
Mensaje modificado por EnemyOfGod286 el Aug 28 2010, 08:34 PM |
|
|
|
 Aug 28 2010, 08:32 PM Aug 28 2010, 08:32 PM
Publicado:
#2
|
|
 Dios Matemático Supremo Grupo: Usuario FMAT Mensajes: 858 Registrado: 20-August 09 Desde: In my House Miembro Nº: 57.323 Nacionalidad:  Colegio/Liceo:  Universidad:  Sexo:  |
P3
Primero, para no tener problemas de desigualdades veremos el comportamiento de 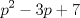 y y 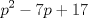 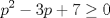 Discriminante: 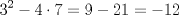 , luego para cualquier valor de , luego para cualquier valor de 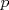 , la expresión sera positiva. Es decir siempre se cumple que , la expresión sera positiva. Es decir siempre se cumple que 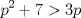 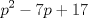 Discriminante: 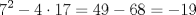 por lo que tambien para cualquier valor de por lo que tambien para cualquier valor de 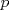 la expresion es positiva. Por lo que siempre se cumple que la expresion es positiva. Por lo que siempre se cumple que 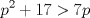 Luego vemos que los primos mayores que 10 terminan en 1,3,7,9 luego vemos las terminanciones de estos en ambas expresiones. Cuando p termina en 1,3,7,9, 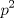 termina en 1,9,9,1, por lo que termina en 1,9,9,1, por lo que 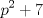 termina en 8,6,6,8 termina en 8,6,6,8Cuando p termina en 1,3,7,9 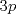 termina en 3,9,1,7 termina en 3,9,1,7Luego 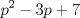 termina en 5,7,5,1 termina en 5,7,5,1Por lo que los primos que terminan en 1 y en 7 no nos sirven Vemos que ocurre con los que terminan en 3 y 9 en la otra expresion Cuando p termina en 3,9 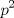 termina con 9,1, luego termina con 9,1, luego 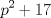 termina en 6,8 termina en 6,8Cuando p termina en 3,9 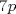 termina en 1,3 termina en 1,3Por lo que 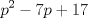 termina en 5,5 termina en 5,5Por lo que descartamos todos los primos mayores que 10 y las soluciones únicas son 2,3,5 dando los primos (5,7);(7,5);(17,7) Mensaje modificado por EnemyOfGod286 el Aug 28 2010, 08:53 PM |
|
|
|
 Aug 28 2010, 08:43 PM Aug 28 2010, 08:43 PM
Publicado:
#3
|
|
|
Principiante Matemático Grupo: Usuario FMAT Mensajes: 2 Registrado: 28-August 10 Miembro Nº: 76.196 |
Yo la hice...,la 2) me dio 296 la 3) me dio 2 y 3, la 5 (2,2) y (2,3), la 6) que los circulos debían ser eactamente iguales, la respuesta de las otras es muy larga...
|
|
|
|
 Aug 28 2010, 09:39 PM Aug 28 2010, 09:39 PM
Publicado:
#4
|
|
 Doctor en Matemáticas Grupo: Usuario FMAT Mensajes: 143 Registrado: 6-February 08 Desde: desde aquí Miembro Nº: 15.300 Nacionalidad:  Colegio/Liceo:  Sexo:  |
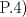 Estaba en plena demostración inductiva cuando me iluminé y dije "que tal si" Estaba en plena demostración inductiva cuando me iluminé y dije "que tal si"Para  entonces entonces 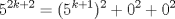 Luego dije mmm y que pasa si es impar? entonces para Luego dije mmm y que pasa si es impar? entonces para 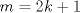 entonces entonces 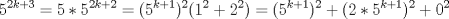 Ahí me reí solo un rato y segui la demostracion por induccion, despues puse como solucion alternativa eso de arriba xDDDD Mensaje modificado por Aheit el Aug 28 2010, 09:40 PM -------------------- |Ente Inmiscible|  |
|
|
|
 Aug 28 2010, 09:45 PM Aug 28 2010, 09:45 PM
Publicado:
#5
|
|
 Doctor en Matemáticas Grupo: Usuario FMAT Mensajes: 160 Registrado: 27-May 09 Desde: Santiago Miembro Nº: 52.384 Nacionalidad:  Universidad:  Sexo:  |
^Yo igual estaba con la demostracion inductiva y me ilumine con eso!! xD!! wenisima, pero yo borre la inductiva y puse esa, que me parecia mas simple, solo que eso de que 0 es cuadrado perfecto no lo usé, me parecio muy sucio, lo hice con 125 = 100 + 16 + 9 y 625 = 256 + 144 + 225
Mensaje modificado por Rurouni Kenshin el Aug 28 2010, 11:49 PM |
|
|
|
 Aug 28 2010, 09:46 PM Aug 28 2010, 09:46 PM
Publicado:
#6
|
|
 Dios Matemático Supremo Grupo: Usuario FMAT Mensajes: 858 Registrado: 20-August 09 Desde: In my House Miembro Nº: 57.323 Nacionalidad:  Colegio/Liceo:  Universidad:  Sexo:  |
^Yo igual estaba con la demostracion inductiva y me ilumine con eso!! xD!! wenisima, pero yo borre la inductiva y puse esa, que me parecia mas simple, solo que eso de que 0 es cuadrado perfecto no lo usé, me parecio muy sucio, lo hice con 125 = 100 + 16 + 9 y 625 = 296 + 144 + 225 256 no 296 saludos |
|
|
|
 Aug 28 2010, 09:47 PM Aug 28 2010, 09:47 PM
Publicado:
#7
|
|
 Doctor en Matemáticas Grupo: Usuario FMAT Mensajes: 160 Registrado: 27-May 09 Desde: Santiago Miembro Nº: 52.384 Nacionalidad:  Universidad:  Sexo:  |
|
|
|
|
 Aug 28 2010, 09:48 PM Aug 28 2010, 09:48 PM
Publicado:
#8
|
|
 Doctor en Matemáticas Grupo: Usuario FMAT Mensajes: 143 Registrado: 6-February 08 Desde: desde aquí Miembro Nº: 15.300 Nacionalidad:  Colegio/Liceo:  Sexo:  |
^Yo igual estaba con la demostracion inductiva y me ilumine con eso!! xD!! wenisima, pero yo borre la inductiva y puse esa, que me parecia mas simple, solo que eso de que 0 es cuadrado perfecto no lo usé, me parecio muy sucio, lo hice con 125 = 100 + 16 + 9 y 625 = 296 + 144 + 225 Esque elñ problema decía "como la suma de tres cuadrados de numeros enteros" y el 0 pertenece a los 
-------------------- |Ente Inmiscible|  |
|
|
|
 Aug 28 2010, 10:25 PM Aug 28 2010, 10:25 PM
Publicado:
#9
|
|
|
Webmaster Grupo: Administrador Mensajes: 6.692 Registrado: 13-May 05 Desde: Santiago Centro Miembro Nº: 2 Nacionalidad:  Sexo:  |
CITA Problema 3: Encuentre todos los números primos 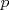 tales que tales que 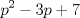 y y 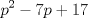 son también primos son también primosPara la P3, aqui va una visión alternativa. Para p=2, 3 y 5 funciona Para p primo, con 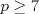 , demostraremos que alguno de los otros dos números será un múltiplo de 5 mayor a 5, por lo cuál no será primo. , demostraremos que alguno de los otros dos números será un múltiplo de 5 mayor a 5, por lo cuál no será primo.Demostración Saludos PD: Por supuesto la solución es "informal", pero es suficiente para que el alumno pueda entenderla (y esa es la idea -------------------- Colegios/Liceos/Universidades en Fmat (Integrate!!!!)
Videos PSU de Funciones (Y tú, ¿Aun estas aproblemado con Funciones?)   |
|
|
|
 Aug 28 2010, 10:37 PM Aug 28 2010, 10:37 PM
Publicado:
#10
|
|
 Dios Matemático Supremo Grupo: Moderador Mensajes: 590 Registrado: 14-October 07 Miembro Nº: 11.310 Colegio/Liceo:  Universidad:  Sexo:  |
Una forma sin piedad de matar el P1:
Saludos. PD: Era por si querian una solución corta. xD -------------------- |
|
|
|
  |
1 usuario(s) está(n) leyendo esta discusión (1 invitado(s) y 0 usuario(s) anónimo(s))
0 miembro(s):
| Versión Lo-Fi | Fecha y Hora actual: 20th October 2025 - 07:58 AM |












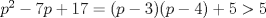
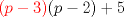 será divisible en 5 (se puede factorizar por 5, pues
será divisible en 5 (se puede factorizar por 5, pues 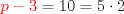 ).
). 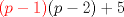 será divisible por 5 (se puede factorizar por 5, pues
será divisible por 5 (se puede factorizar por 5, pues 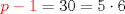 ).
).