|
|
|
|
|
|
|
  |
 Aug 8 2010, 06:01 PM Aug 8 2010, 06:01 PM
Publicado:
#1
|
|
 Dios Matemático Supremo Grupo: Administrador Mensajes: 2.706 Registrado: 13-May 05 Desde: Santiago de Chile Miembro Nº: 10 Nacionalidad:  Colegio/Liceo:  Sexo:  |
Dada la secuencia:Nota: Los colores de los triángulos externos se alternan.
-------------------- |
|
|
|
 Aug 8 2010, 06:06 PM Aug 8 2010, 06:06 PM
Publicado:
#2
|
|
|
Dios Matemático Supremo Grupo: Usuario FMAT Mensajes: 9.897 Registrado: 6-April 08 Miembro Nº: 19.238 Nacionalidad:  Colegio/Liceo:  Sexo:  |
habra ud notado que los triangulos perifericos de las figuras pares son negros, luego el nro 2010 tendrá triangulos negros afuerita.
para contarlos simplemente observe ud que es la tabla del nueve atrasada en 1, asi que la figura 2010 tendra 2009X9 triangulitos. la parte B lo unico que pedia era que ud escribiera Tn=9(n-1)+T(n-2) (donde Tn=triangulos perifericos de la figura "n") sustituyendo el valor de todos los T tenemos finalmente Tn=9(1+2+3+4+...+(n-1))=4.5n(n-1) Mensaje modificado por Kaissa el Aug 8 2010, 06:11 PM -------------------- |
|
|
|
 Aug 8 2010, 06:09 PM Aug 8 2010, 06:09 PM
Publicado:
#3
|
|
 Dios Matemático Supremo Grupo: Administrador Mensajes: 2.706 Registrado: 13-May 05 Desde: Santiago de Chile Miembro Nº: 10 Nacionalidad:  Colegio/Liceo:  Sexo:  |
En la parte a, hay un leve error de conteo. Por ejemplo, en la figura 2 de la secuencia hay 9 x 1 triángulos.
En la parte b no basta con los triángulos externos, deben ser contados todos los triángulos. En todo caso, creo que para ser problema de tercero era un "regalo"... -------------------- |
|
|
|
 Aug 8 2010, 06:11 PM Aug 8 2010, 06:11 PM
Publicado:
#4
|
|
|
Dios Matemático Supremo Grupo: Usuario FMAT Mensajes: 9.897 Registrado: 6-April 08 Miembro Nº: 19.238 Nacionalidad:  Colegio/Liceo:  Sexo:  |
editado
-------------------- |
|
|
|
 Aug 8 2010, 06:50 PM Aug 8 2010, 06:50 PM
Publicado:
#5
|
|
 Dios Matemático Grupo: Usuario FMAT Mensajes: 270 Registrado: 31-May 10 Desde: San antonio Miembro Nº: 71.730 Nacionalidad:  Colegio/Liceo:  Universidad:  Sexo:  |
yo la parte b la hise de diferente manera la mostrare.

Mensaje modificado por luis_fz el Aug 8 2010, 06:51 PM |
|
|
|
 Aug 9 2010, 10:00 PM Aug 9 2010, 10:00 PM
Publicado:
#6
|
|
|
Principiante Matemático Grupo: Usuario FMAT Mensajes: 14 Registrado: 24-October 09 Desde: santiago Miembro Nº: 60.849 Nacionalidad:  Colegio/Liceo:  Sexo:  |
Yo soy de segundo medio, un amigo de III medio me lo paso y en clase lo hice (el b):
Notemos que: En la figura 1 hay una fila, lo que corresponde a 1 triangulo En la figura 2 hay 3 filas mas y en cada fila aumenta en 1 el numero de triangulos, en total 10 En la figura 3 hay 3 filas mas, en total 28 triangulos. Podemos aplicar la formula para determiar el numero de filas (ya que en cada figura aumenta en 3): 1 -> 1+3(1-1)=1 2 -> 1+3(2-1)=4 3 -> 1+3(3-1)=7 .... 2010 -> 1+3(2010-1) = 1+3*2009= 6028 Ademas notemos que el numero de triángulos aumenta en uno por cada fila, por lo que podriamos aplicar una de las formulas de la sumatoria (desde 1 hazta n) 1-> 1(1+1)/2=1 2-> 4(4+1)/2=10 3-> 7(7+1)/2=28 .... 2010-> 6028(6029)/2= 3014*6029 Creo que el ejercicio bastará con dejar la solución indicada Mensaje modificado por Kuky el Aug 9 2010, 10:01 PM |
|
|
|
 Apr 23 2011, 04:20 PM Apr 23 2011, 04:20 PM
Publicado:
#7
|
|
 Doctor en Matemáticas Grupo: Usuario FMAT Mensajes: 193 Registrado: 22-March 07 Desde: San Miguel, Santiago Miembro Nº: 4.651 Nacionalidad:  Colegio/Liceo:  Universidad:  Sexo:  |
1- Por paridad claramente la figura
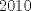 tiene triángulos exteriores de color negro. Notemos que al pasar de figura en figura, al lado se le agregan tiene triángulos exteriores de color negro. Notemos que al pasar de figura en figura, al lado se le agregan  triángulos, así que el lado de la figura triángulos, así que el lado de la figura  sera sera 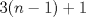 . Cada figura tiene . Cada figura tiene  lados, pero cada lado uno a uno se intersecta con otro en lados, pero cada lado uno a uno se intersecta con otro en 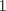 triangulo, asi que la cantidad de triangulos externos de la figura triangulo, asi que la cantidad de triangulos externos de la figura  sera sera 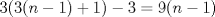 . Para . Para 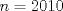 tendremos tendremos 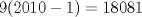 triángulos externos. triángulos externos.2- Notemos que desde un lado a su vértice opuesto los triángulos cumplen una sucesión aritmética de diferencia 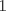 . Asi que si el lado de la figura . Asi que si el lado de la figura  era era 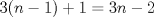 , esta tendrá en total , esta tendrá en total 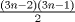 . Por lo tanto para . Por lo tanto para 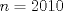 se tendrán se tendrán 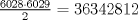 triángulos. triángulos.
-------------------- |
|
|
|
 Apr 23 2011, 04:21 PM Apr 23 2011, 04:21 PM
Publicado:
#8
|
|
 Doctor en Matemáticas Grupo: Usuario FMAT Mensajes: 193 Registrado: 22-March 07 Desde: San Miguel, Santiago Miembro Nº: 4.651 Nacionalidad:  Colegio/Liceo:  Universidad:  Sexo:  |
A resueltos porfavor.
-------------------- |
|
|
|
 Nov 26 2011, 04:02 PM Nov 26 2011, 04:02 PM
Publicado:
#9
|
|
|
Matemático Grupo: Validating Mensajes: 50 Registrado: 22-October 11 Desde: Santiago Miembro Nº: 96.078 Nacionalidad:  Colegio/Liceo:  Sexo:  |
2- Notemos que desde un lado a su vértice opuesto los triángulos cumplen una sucesión aritmética de diferencia 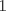 . Asi que si el lado de la figura . Asi que si el lado de la figura  era era 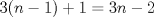 , esta tendrá en total , esta tendrá en total 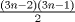 . Por lo tanto para . Por lo tanto para 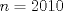 se tendrán se tendrán 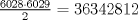 triángulos. triángulos.[/quote] La respuesta final a esa pregunta es 18.171.406 triángulos, se te olvido partir en 2. |
|
|
|
  |
1 usuario(s) está(n) leyendo esta discusión (1 invitado(s) y 0 usuario(s) anónimo(s))
0 miembro(s):
| Versión Lo-Fi | Fecha y Hora actual: 23rd November 2024 - 04:28 PM |












