CMAT 2010 - Fecha 4 - Nivel 4 Individual

Foro fmat.cl > Sector Preparación Olimpiadas > Competencias y Olimpiadas > Campeonato Interescolar > Campeonato Interescolar 2010 > Cuarta Fecha

CMAT 2010 - Fecha 4 - Nivel 4 Individual

Opciones

S. E. Puelma Moy... S. E. Puelma Moya Ver Perfil del Miembro Ver los mensajes de este miembro	Aug 8 2010, 12:03 AM Publicado: #1
Dios Matemático Supremo Grupo: Administrador Mensajes: 2.706 Registrado: 13-May 05 Desde: Santiago de Chile Miembro Nº: 10 Nacionalidad: Colegio/Liceo: Sexo:	VIII CAMPEONATO ESCOLAR DE MATEMÁTICA - CMAT Fecha 4: Sábado 7 de Agosto de 2010 Cuarto Nivel Individual Problema 1 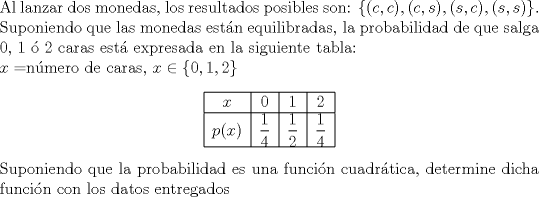$TEX: \noindent Al lanzar dos monedas, los resultados posibles son: $\{(c,c),(c,s),(s,c),(s,s)\}$. Suponiendo que las monedas están equilibradas, la probabilidad de que salga 0, 1 ó 2 caras está expresada en la siguiente tabla:<br /><br />\noindent$x=$número de caras, $x\in\{0,1,2\}$<br />\begin{center}<br />\begin{tabular}{\|c\|c\|c\|c\|}<br />\hline<br />$x$&0&1&2\\ \hline<br />$p(x)$&$\dfrac14$&$\dfrac12$&$\dfrac14$\\ \hline<br />\end{tabular}<br />\end{center}<br /><br />\noindent Suponiendo que la probabilidad es una función cuadrática, determine dicha función con los datos entregados$ Problema 2 $TEX: \noindent Es dada una circunferencia $C_r(P)$, con centro $P$ y radio $r$. Sean $E_n(r,P)$ y $e_n(r,P)$ polígonos regulares con $n$ lados, el primero de ellos admite a $C_r(P)$ como circunferencia inscrita y el segundo de ellos admite a $C_r(P)$ como circunferencia circunscrita.<br /><br />\noindent Sea $[F]$ el área de la figura plana $F$<br />\begin{itemize}<br />\item[$a)$](3 puntos) Determine $A_n(r,P)=[E_n(r,P)]-[C_r(P)]$<br />\item[$b)$](3 puntos) Determine $a_n(r,P)=[C_r(P)]-[E_n(r,P)]$<br />\item[$c)$](2 puntos) Sabiendo que para $\theta$ pequeño, medido en radianes, vale $\tan(\theta)\approx\theta+\dfrac{\theta^3}3$, encuentre el menor número $n$, en función de $r$, tal que $A_n(r,P)<10^{-3}$<br />\item[$d)$](2 puntos) Sabiendo que para $\theta$ pequeño, medido en radianes, vale $\sin(\theta)\approx\theta-\dfrac{\theta^3}6$, encuentre el menor número $n$, en función de $r$, tal que $a_n(r,P)<10^{-3}$<br />\end{itemize}<br />\textbf{Nota:} Recuerde que, cuando los ángulos se miden en radianes, $360^\circ$ equivale a $2\pi$ y $180^\circ$ equivale a $\pi$$ -------------------- Sebastián Elías Puelma Moya Administrador FMAT