EDP - Foro fmat.cl

Portal Matemático

¿Qué es FMAT?

Foro fmat.cl > Programa Enseñanza Universitaria > Ejercitación > Ecuaciones Diferenciales > EDP

Reply to this topic

Start new topic

EDP

josftx Ver Perfil del Miembro Ver los mensajes de este miembro	Jul 14 2010, 07:34 PM Publicado: #1
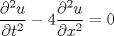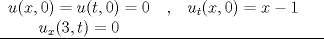Maestro Matemático Grupo: Usuario FMAT Mensajes: 129 Registrado: 2-September 08 Desde: Curicó Miembro Nº: 33.750 Nacionalidad: Universidad: Sexo:	Resolver la ecuacion , hallando la solucion como una serie de fourier y expresando sus coeficientes en terminos de n. $TEX: $\displaystyle \frac{\partial^{2} u}{\partial t^{2}}-4\frac{\partial^{2} u}{\partial x^{2}}=0$$ $TEX: \begin{tabular}{ccccc\|}<br />$u(x,0)=u(t,0)=0$ & , & $ u_{t}(x,0)=x-1$& \\<br />$u_{x}(3,t)=0$ \\ \hline<br />\end{tabular}$ con t>0 y 0<x<3

Abu-Khalil Ver Perfil del Miembro Ver los mensajes de este miembro	Jul 14 2010, 09:28 PM Publicado: #2
Dios Matemático Supremo Grupo: Usuario FMAT Mensajes: 3.812 Registrado: 4-November 07 Desde: Santiago Miembro Nº: 12.213 Nacionalidad: Colegio/Liceo: Universidad: Sexo:	$TEX: \noindent Buscamos una solución de la forma<br />\begin{equation}<br />u(x,t)=f(x)g(t).<br />\end{equation}<br />Se tiene que<br />\[fg''=4gf''\Rightarrow \frac{g''}{4g}=\frac{f''}{f}=-\lambda.\]<br />Luego, $f$ satisface<br />\[<br />f''+\lambda f=0,<br />\]<br />con $f(0)=f(3)=0$. Por lo tanto, $f$ es de la forma<br />\begin{equation}f_n(x)=\sin\left(\frac{n\pi}{3}x\right),\quad n\in\mathbb{N}.\end{equation}<br />Así, $g$ debe satisfacer<br />\[g''+4\lambda g=0,\]<br />con $g(0)=0$. Sigue que<br />\[g_n(t)=\sin\left(\frac{2n\pi}{3}t\right).\]<br />Por ende,<br />\[u(x,t)=\sum_{n=1}^\infty a_n\sin\left(\frac{2n\pi}{3}t\right)\sin\left(\frac{n\pi}{3}x\right).\]<br />Finalmente, imponiendo que<br />\[u_t(x,0)=\sum_{n=1}^\infty a_n\frac{2n\pi}{3}\sin\left(\frac{n\pi}{3}x\right)=x-1,\]<br />se tiene que<br />\[\frac{2n\pi}{3}a_n=\frac{2}{3}\int_0^3(x-1)\sin\left(\frac{n\pi}{3}x\right)dx\Rightarrow a_n=-\frac{3}{n^2\pi^2}\left(1+2\cos(n\pi)\right),\]<br />es decir,<br />\[a_n=\begin{cases}<br />-\dfrac{9}{n^2\pi^2},\text{ si }n\text{ es par}\\<br />\\<br />\dfrac{3}{n^2\pi^2},\text{ si }n\text{ es impar}<br />\end{cases}.\qquad \square\]<br />$ -------------------- ~milopez $TEX: \[\mathfrak{L}=\int_{-\infty}^\infty e^{-289x^2}dx=\frac{\Gamma (\frac{1}{2})}{17}=\frac{\sqrt{\pi}}{17}\]$ $TEX: <br />\begin{equation}\begin{aligned}<br />dS_t&=\mu S_t dt+\sqrt{V_t}S_t dW^S_t\\<br />dV_t&=\kappa(\theta-V_t)dt+\sigma\sqrt{V_t} dW^V_t\\<br />\end{aligned}\end{equation}<br />$ $TEX: <br />$$\mathbb A^{\text U}_M(N)$$<br />$

josftx Ver Perfil del Miembro Ver los mensajes de este miembro	Jul 15 2010, 04:57 PM Publicado: #3
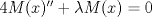Maestro Matemático Grupo: Usuario FMAT Mensajes: 129 Registrado: 2-September 08 Desde: Curicó Miembro Nº: 33.750 Nacionalidad: Universidad: Sexo:	que pasa si no estan esos intervalos t>0 y 0<x<3 ?, en el ejercicio que tengo yo, por el cual escribi, no aparecen esos limites. y yo los agrege suponiendo que podrian ser. 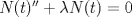$TEX: $4M(x)''+\lambda M(x)=0$$ $TEX: $N(t)''+\lambda N(t)=0$$ por consiguiente las soluciones son: 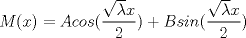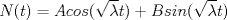$TEX: $\displaystyle M(x)=Acos(\frac{\sqrt{\lambda }x}{2})+Bsin (\frac{\sqrt{\lambda }x}{2})$$ $TEX: $\displaystyle N(t)=Acos(\sqrt{\lambda }t)+Bsin (\sqrt{\lambda }t)$$ con las condiciones iniciales. 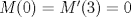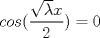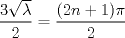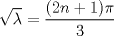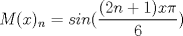$TEX: $M(0)=M'(3)=0$$ $TEX: $\displaystyle cos(\frac{\sqrt{\lambda }x}{2})=0$$ $TEX: $\displaystyle \frac{3\sqrt{\lambda }}{2}=\frac{(2n+1)\pi}{2}$$ $TEX: $\displaystyle \sqrt{\lambda }=\frac{(2n+1)\pi}{3}$$ $TEX: $\displaystyle M(x)_{n}=sin(\frac{(2n+1)x\pi}{6})$$ con eso cambia toda la solucion que pusise Abu. no se lee bien creo el U sub x. Mensaje modificado por josftx el Jul 15 2010, 05:09 PM

Lledó Ver Perfil del Miembro Ver los mensajes de este miembro	Jun 20 2018, 12:17 AM Publicado: #4
Principiante Matemático Grupo: Usuario FMAT Mensajes: 8 Registrado: 10-September 16 Desde: Temuco de Chile Miembro Nº: 147.372 Nacionalidad: Colegio/Liceo: Universidad: Sexo:	CITA(Abu-Khalil @ Jul 14 2010, 10:28 PM) $TEX: \noindent Buscamos una solución de la forma<br />\begin{equation}<br />u(x,t)=f(x)g(t).<br />\end{equation}<br />Se tiene que<br />\[fg''=4gf''\Rightarrow \frac{g''}{4g}=\frac{f''}{f}=-\lambda.\]<br />Luego, $f$ satisface<br />\[<br />f''+\lambda f=0,<br />\]<br />con $f(0)=f(3)=0$. Por lo tanto, $f$ es de la forma<br />\begin{equation}f_n(x)=\sin\left(\frac{n\pi}{3}x\right),\quad n\in\mathbb{N}.\end{equation}<br />Así, $g$ debe satisfacer<br />\[g''+4\lambda g=0,\]<br />con $g(0)=0$. Sigue que<br />\[g_n(t)=\sin\left(\frac{2n\pi}{3}t\right).\]<br />Por ende,<br />\[u(x,t)=\sum_{n=1}^\infty a_n\sin\left(\frac{2n\pi}{3}t\right)\sin\left(\frac{n\pi}{3}x\right).\]<br />Finalmente, imponiendo que<br />\[u_t(x,0)=\sum_{n=1}^\infty a_n\frac{2n\pi}{3}\sin\left(\frac{n\pi}{3}x\right)=x-1,\]<br />se tiene que<br />\[\frac{2n\pi}{3}a_n=\frac{2}{3}\int_0^3(x-1)\sin\left(\frac{n\pi}{3}x\right)dx\Rightarrow a_n=-\frac{3}{n^2\pi^2}\left(1+2\cos(n\pi)\right),\]<br />es decir,<br />\[a_n=\begin{cases}<br />-\dfrac{9}{n^2\pi^2},\text{ si }n\text{ es par}\\<br />\\<br />\dfrac{3}{n^2\pi^2},\text{ si }n\text{ es impar}<br />\end{cases}.\qquad \square\]<br />$ Como llegaste a que f(3) = 0 ??? Porque yo llegué a que f'(3) = 0.... -------------------- *Hay que tener la mente abierta. Pero no tanto como para que se te caiga el cerebro.* R.Feynman.

« Posterior · EDP · Anterior »

Reply to this topic

Start new topic

1 usuario(s) está(n) leyendo esta discusión (1 invitado(s) y 0 usuario(s) anónimo(s))

0 miembro(s):

Versión Lo-Fi

Fecha y Hora actual: 9th April 2025 - 04:07 PM

Powered By IP.Board 2.2.1 © 2007 IPS, Inc.