CITA(DressedToKill @ May 21 2010, 10:44 PM)
Y cual es el problema con que alguien quiera ganar plata? No puedes esperar que todos los humanos sean superheroes de la ciencia.
CITA(One of this days @ Jan 31 2011, 12:22 PM)
Por eso es claro que la universidad no es para todos.
CITA(Kura @ Feb 1 2011, 02:05 AM)
Es re peluo ser médico por la plata. Si hasta los que entran por vocación se aburren de la gente que va al consultorio a preguntar xq le duele la guata el 1 de enero luego de tomarse 50 copetes y 40 empanadas.
CITA(Pasten @ Mar 17 2011, 10:29 AM)
Mi respuesta: a mi que me importa, yo ya sali.
Eso, espero que mi respuesta te ayude.
Saludos
CITA(mmxmaster! @ Mar 23 2011, 08:53 PM)
Dejen de hacer esta prueba porque no mide nada... a menos que salga su universidad en primer lugar. Otra guerra santa.
CITA(florindo @ Mar 26 2011, 12:28 AM)
Las matemáticas son hermosas cuando se piensa no cuando sólo se alguna receta sino sería muy facil estudiarla.
CITA(mmxmaster! @ May 30 2011, 02:59 AM)
Parece que de aquí a 10 años más no van a haber carreras pa estudiar, porque todas van a estar saturadas... me sorprende la poca proyección de los estudiantes.
CITA(Gastón Burrull @ Jun 24 2011, 10:39 PM)
el 0 no existe.. es marketing para que la gente estudie matemáticas...
CITA(Abu-Khalil @ Jul 4 2011, 01:49 PM)
Comercial no es una Ingeniería :ridi:
CITA(Kura @ Sep 29 2011, 10:05 PM)
xDDD, que notable como aquí pareciese haber una disputa sobre quien sabe más y quien impone su opinión sobre otro.
Alguien sabe mas de Relatividad aparte de lo que leyo en wikipedia xd?
CITA(CRLeonardo @ Nov 5 2011, 02:26 AM)
Son pocas las universidades en Chile que tienen programas de postgrados en ciencias puras o aplicadas. El resto no merece llamarse universidad.
CITA(Sansanito @ Nov 20 2011, 02:54 PM)
En la vida las metas tienen que ser grandes.... solo grandes? ....nononono..... LAS METAS TIENEN QUE SER GIGANTEEEES.. ENORMEEEEEEES...
Tu meta final no puede ser estudiar en la UTFSM, en la PUC o en la Chile.. esas son pequeñeces..incluso estudiar en la mejor U de USA, Inglaterra, Alemania o Suiza.. todas son pequeñeces que muchos logran... cosas vacías.. que alcanzas con cuanto?.. 18?.. 20?.. 25??... y que haces el resto de la vida??
CITA(Kura)
A mi me gustaría ser genio, asi me auto cumpliría deseos, o me iría a trollear a la gente ofreciéndole deseos y si no dicen las cosas explícitamente bien, cagarlos xd.
CITA(lokko62 @ Jan 9 2012, 02:27 AM)
Estimado, este es un foro de matemáticas, no de gente que se cree maple-humanos.
¿Sirve tanto saber resolver cuárticas con trucos raros, siendo que la mayoría de los polinomios ni son solubles por radicales.? Tu cantidad de aplicación es ínfima, si tomas una función al azar nisiquiera le encontrarás primitiva, a tí que te da por integrar todo lo posible cuando las soluciones exactas son lo que menos hay, para qué ponerse a buscar como loco todas las funciones que tienen primitiva, o los polinomios de 4to grado que salen con un truco bonito?, aparte de que no sirve de nada la solución exacta hay programas para hallarlas a fuerza bruta y simplificar y todo eso y evitar el lío.
Aprende a caracterizar polinomios, y no a buscar problema raro por problema raro que encuentres, hay infinitos polinomios feos o bonitos que te hacen la gracia que quieres, y hay una cantidad enormemente más grande de los que no hacen la gracia.
Mejor ponte a estudiar geometría algebraica para estudiar los ceros de los polinomios (y en varias variables además) y caracterizarlos decentemente, ubícate, este es un foro más decente.
CITA(Krauser @ Jan 12 2012, 09:51 PM)
tienes q terminar el pokemon amarillo con un pikachu nivel 5 100 veces (si sube de nivel no sirve) y luego quemar tu casa con fosforos, cuando lo hagas prende tu gameboy y apenas pises el pasto aparecera deoxys nivel 102 salvaje, ahi le tiras la masterball. Una vez capturado, tendras ke ir al gimnasio de brock (solo se abrira la puerta si tienes a deoxys) el cual tendra alas y dira "brock alado quiere luchar", ten cuidado porke tiene 6 pokemones level 150 (un onix, golem, mewtwo, mew, rayquaza y rhyperior) cuando lo derrotes te dira "esto aun no acaba" explota y aparece yugi retandote a un duelo de cartas, puedes responderle "SI" o "NO" (por ahora responde no porque debemos conseguir un mazo de cartas primero).
Dirigete a ciudad fucsia y entra a la zona safari, y vas donde el tipo que te daba el surf, pero ahora te dara un mazo de cartas, apareceran 3 opciones:
-Mazo Exodia
-Mazo Slifer
-Mazo Alado de Ra
Elige el mazo exodia y reta a yugi hasta qe te aparezcan las partes de exodia para hacerlo mas facil ;) una vez derrotado te dara su carta kuriboh, la cual se la tienes que intercambiar a giovanni (el del octvo gimnasio) por el libro de las universidades, en el cual aparecen las universidades que quedaste, los puntajes de corte de todas las carreras y ****.
Ojala te haya ayudado, cualquier duda preguntas
Saludos!!
CITA(mmxmaster! @ Feb 18 2012, 12:17 PM)
Y dale con el pituto, ¿pa que estudian si al final van a ser unos fracasados sin pituto?
CITA(Gastón Burrull @ Feb 29 2012, 09:46 PM)
Como servicios, puedo ofrecer clases, imitación de lindorfo, bailar (sí, bailar), pueden usar mis servicios en el momento que quieran en la junta, total el servicio lo pagan todos.
Tengo silla portátil, portapapeles, portalápices y una papelera, más una mesa portátil, así que puedo transformar en segundos y sin cargar desde mi casa mucho peso cualquier lugar en una oficina, ustedes se sientan adelante y hago las clases a pedido , física. matemáticas, etcétera. Me lo pueden pedir incluso bailando y no creo que pro este servicio la cuota suba mucho, quizás les cueste 100 pesos por cabeza, es más barato que contratar a shakira.
Saludos.
CITA(Pasten @ Apr 12 2012, 10:34 PM)
Puede ser, dado que arxiv partio en 1991. En todo caso la investigacion en ciencia funciona asi:
Haces tu investigacion, y si llegas a una conclusion importante entonces lo comentas con la gente que podria interesarle. La cosa es que al par de dias todos a quienes podria interesarles de verdad y podrian entender lo que hiciste, ya lo saben. Los unicos que realmente se enteran por medio de revistas son los mortales comunes y silvestres que no son expertos en tu tema, o los administrativos del gobierno encargados de entregar becas (esos si son los unicos realmente interesados en el asunto de las revistas). Generalmente en las revistas solo aparecen versiones muy resumidas y livianitas de las investigaciones de verdad.
Pero si los hace felices, sigamos pensando que los chilenos somos ultra bacanes y los gringos nos robaron una idea genial.
Yo soy Pasten y descarto los planetas que se me da la gana. Es mas, desde ahora declaro que Venus ya no es planeta, dandole la razon a Hegel.
CITA(Maxooon @ Apr 19 2012, 11:46 PM)
Lema: Las inteligencias no se anulan
Demostración: Sean A y B dos inteligencias. Supongamos por absurdo que A anula a B. Como B es inteligencia, en particular existe al menos un problema que puede resolverse en B. Pero por hipótesis A anula a B, y por lo tanto
el problema no tiene resolución, lo que contradice el hecho de que B es inteligencia. Q.E.D
CITA(Kura @ May 1 2012, 06:43 PM)
No se a mi la matemática nunca me ha parecido ciencia, la verdad no se, para mi es esencial poder hacer experimentos en el mundo real para llamarlo ciencia, ahora que se yo si la matemática va a un lab y reitera experimentos hartas veces. No es que me interese saber la definición de ciencia ni nada, me quedo con la custión de Descartes y punto xd.
Aunque ni idea, yo soy Ingeniero, y eso no es ciencia (aunq le pongamos nombres choros como Ciencia Aplicada para sentirnos bknes), me preocupo por ganar plata nomá.
Examen 1-2010, By I. Huerta & G. Raykov
Foro fmat.cl > Programa Enseñanza Universitaria > Comunidades Universitarias > Universidad Católica > Ecuaciones Diferenciales
Jul 1 2010, 03:12 PM
![TEX: <br />\begin{enumerate}<br />\item <br />\begin{itemize} <br />\item[(a)] Resuelva $y'=\frac{2}{x}y-y^2, \: y(1)=1$.<br />\item[(b)] Resuelva $x+yy'=\left(x^2+y^2\right)^{\frac{1}{2}}, \: y(1)=1$.<br />\item[©] Justifique la unicidad de la solución para el problema de valor inicial $xy'=y^2, \: y(1)=1$. ¿Para cuáles valores de $a$, $b$ el problema con condiciones iniciales $y(a)=b$ no tiene solución?.<br />\end{itemize}<br />\item Sea $$A = \left[ \begin{array}{cc} 2 & 1 \\ -1 & 2 \end{array} \right].$$<br />\begin{itemize} <br />\item[(a)] Calcule la matriz $e^{tA}, \: t \in \mathbb{R}$.<br />\item[(b)] Resuelva el problema de Cauchy $$\vec{x}'=A\vec{x} + \left[ \begin{array}{c} 0 \\ e^{2t} \end{array} \right], \quad \vec{x}(0) = \left[ \begin{array}{c} 0 \\ 0 \end{array} \right].$$<br />\end{itemize}<br />\item Para la ecuación diferencial $y'=(y-1)\sin{(y^2)}$<br />\begin{itemize} <br />\item[(a)] Determine y clasifique sus puntos de equilibrio.<br />\item[(b)] Para $y(t)$ solución de la EDO, con $y(0)=a$, dependiendo del valor de $a$, con $-2<a<2$, determine $L_1=\lim_{t\rightarrow \infty} y(t), \: L_2=\lim_{t\rightarrow -\infty} y(t)$<br />\end{itemize}<br />\item<br />\begin{itemize}<br />\item[(a)] Resuelva la ecuación integral $$y(t)=-2\int_0^t(t-\tau)y(\tau)d\tau + H(t-2)+1,$$<br />donde $H(t) = \left\{ \begin{array}{lcr} 1 & \mathrm{si} & t \geq 0 \\ 0 & \mathrm{si} & t < 0 \end{array} \right.$<br />\item[(b)] Resuelva el problema de valor inicial $$x''(t)+4x(t)=\sin{(2t)} + \delta(t-4\pi), \quad x(0)=x'(0)=1,$$ donde $\delta(t)$ es la función de Dirac.<br />\end{itemize}<br />\end{enumerate}<br />](./tex/7c2b029cb61e3e504cc2f36b3c791545.png)
![TEX: \noindent Notemos que<br />\[A=\begin{bmatrix}<br />2&0\\<br />0&2<br />\end{bmatrix}+\begin{bmatrix}<br />0&1\\<br />-1&0<br />\end{bmatrix}:=2I+B.\]<br />Por lo tanto, como son bonitas,<br />\[e^{At}=e^{2It+Bt}=e^{2It}e^{Bt}.\]<br />Por un lado, <br />\[e^{2It}=\begin{bmatrix}<br />e^{2t}&0\\<br />0&e^{2t}<br />\end{bmatrix}=e^{2t}I.\]<br />Por el otro, <br />\[e^{Bt}=I+Bt+\frac{B^2t^2}{2!}+\frac{B^3t^3}{3!}+\frac{B^4t^4}{4!}+\ldots\]<br />pero <br />\[B^2=\begin{bmatrix}<br />-1&0\\<br />0&-1<br />\end{bmatrix}=-I\Rightarrow B^3=-B\Rightarrow B^4=-B^2=I.<br />\]<br />Luego,<br />\[e^{Bt}=I+Bt-I\frac{t^2}{2!}-B\frac{t^3}{3!}+I\frac{t^4}{4!}\ldots=I\cos t+B\sin t=\begin{bmatrix}<br />\cos t&\sin t\\<br />-\sin t&\cos t<br />\end{bmatrix}.<br />\]<br />Finalmente,<br />\[e^{At}=e^{2t}I<br />\begin{bmatrix}<br />\cos t&\sin t\\<br />-\sin t&\cos t<br />\end{bmatrix}=e^{2t}<br />\begin{bmatrix}<br />\cos t&\sin t\\<br />-\sin t&\cos t<br />\end{bmatrix}<br />.\]<br />](./tex/b99e195774da6c3f6ba0648b2e9bd10a.png)
![TEX: \noindent Sabemos que la solución es de la forma<br />\[\begin{bmatrix}<br />x(t)\\<br />y(t)<br />\end{bmatrix}=\int_0^te^{A(t-s)}\begin{bmatrix}<br />0\\<br />e^{2s}<br />\end{bmatrix}ds+e^{At}\begin{bmatrix}<br />0\\<br />0<br />\end{bmatrix}<br />=e^{2t}\int_0^t\begin{bmatrix}<br />\sin (t-s)\\<br />\cos (t-s)<br />\end{bmatrix}ds<br />=e^{2t}\begin{bmatrix}<br />1-\cos t\\<br />\sin t<br />\end{bmatrix}.<br />\]<br />](./tex/762016b785c134559c1abc25515bdc8e.png)
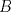es matriz de rotación.
![TEX: \[\mathfrak{L}=\int_{-\infty}^\infty e^{-289x^2}dx=\frac{\Gamma (\frac{1}{2})}{17}=\frac{\sqrt{\pi}}{17}\]](./tex/e0e88dba678ca3ead120b088f41191b2.png)
