CMAT 2010 - Fecha 3 - Nivel 4 Individual

CMAT 2010 - Fecha 3 - Nivel 4 Individual

Opciones

S. E. Puelma Moy... S. E. Puelma Moya Ver Perfil del Miembro Ver los mensajes de este miembro	Jun 27 2010, 09:17 PM Publicado: #1
Dios Matemático Supremo Grupo: Administrador Mensajes: 2.706 Registrado: 13-May 05 Desde: Santiago de Chile Miembro Nº: 10 Nacionalidad: Colegio/Liceo: Sexo:	VIII CAMPEONATO ESCOLAR DE MATEMÁTICA - CMAT Fecha 3: Sábado 26 de Junio de 2010 Primer Nivel Individual Problema 1 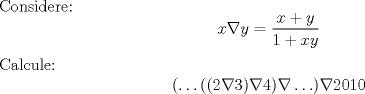$TEX: \noindent Considere:<br />$$x\nabla y=\frac{x+y}{1+xy}$$<br />Calcule:<br />$$(\ldots((2\nabla3)\nabla4)\nabla\ldots)\nabla 2010$$$ Problema 2 $TEX: \noindent Son dadas dos circunferencias tangentes interiormente en el punto $A$. La recta que une los centros de las circunferencias intersecta a la circunferencia exterior e interior en los puntos $C\ne A$ y $B\ne A$, respectivamente. Por el punto medio $M$ de $\overline{BC}$ se levanta la recta perpendicular, que intersecta a la circunferencia exterior en un punto $P$. El segmento $\overline{PA}$ intersecta a la circunferencia interior en el punto $N\ne A$. Demostrar que la recta $MN$ es tangente a la circunferencia menor.$ PARA LAS DUDAS, COMENTARIOS, SOLUCIONES SOBRE CADA PREGUNTA, ACUDIR A LOS TEMAS RESPECTIVOS -------------------- Sebastián Elías Puelma Moya Administrador FMAT