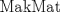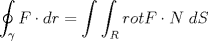|
|
|
|
|
|
|
  |
 Jun 12 2010, 11:20 AM Jun 12 2010, 11:20 AM
Publicado:
#1
|
|
|
Dios Matemático Grupo: Usuario FMAT Mensajes: 400 Registrado: 27-October 09 Desde: ¡Qué te importa! Miembro Nº: 61.057 Universidad:  Sexo:  |
bueno.. Eso.. tuvimos una olimpíada interna.. Estaba fácil y me equivoqué en puras pelotudeces
p1) Se tiene un triángulo de lados 15, 17 y 8. Determine cuánto mide el radio de la circunferencia inscrita p2) Hay dos ciclistas ubicados a 60km de distancia. Estos avanzan con velocidades constantes de 10km/h, en sentidos opuestos. Una hábil e inteligente mosca, que vuela a 30km/h, va de ciclista en ciclista. Determine cuánto recorre la mosquita p3) sea 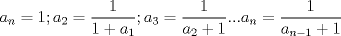 . Determine cuánto es : . Determine cuánto es : 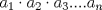 (creo que así era). (creo que así era).p4) Se tiene un número entero de 4 dígitos. i) son todos impares sus dígitos ¡¡) si se divide por 5 queda otro número de 4 dígitos impares ¡¡¡) (no recuerdo bien.. cuando recuerde lo pondré) Determine todos los enteros que cumplen estas condiciones. |
|
|
|
 Jun 12 2010, 11:36 AM Jun 12 2010, 11:36 AM
Publicado:
#2
|
|
|
Dios Matemático Grupo: Usuario FMAT Mensajes: 400 Registrado: 27-October 09 Desde: ¡Qué te importa! Miembro Nº: 61.057 Universidad:  Sexo:  |
Para partir.. Bueno, está bastante fácil en comparación a lo que hacen "los secos".. Jajajaja.. pero igual me costó
Jajaja.. Me gustaría partir por el último, porque, según yo, era el más entretenido Llamemos a este número de 4 dígitos, S. S se puede escribir como = 1000a+100b+10c+d Ahora, también sabemos que tiene que ser divisible por 5. Por lo tanto, es evidente que d debe ser 5 (podría ser 5 o 0, pero cero no es impar). por lo tanto, tendremos un número de la forma 1000a+100b+10c+5 También sabemos que es divisible por 5, o sea, que debe quedarnos además como otro entero de 4 dígitos, también impares si esque dividimos por 5. (podríamos decir que S = 5K) entonces, 5(200a+20b+2c+1)=5K ----> 200a+20b+2c+1=K Pero sabemos que K tiene 4 dígitos, por tanto, 200a sumado con los demás debe ser más de 999. viendo el caso con el mayor valor posible de b, y c, nos queda que 200a = 801. Por tanto, es claro, que a debe ser 5, 7, o 9 (de lo contrario no sería de 4 dígitos el número). Partimos analizando con a=5. 1001+2(10b+c)=K Pero luego sabemos que 2(10b+c) debe ser al menos 110 (sino, quedaría el dígito de las centenas y las decenas con un número no impar). 10b+c>=55 (acá el caso mínimo de b, sería con c=9) por lo tanto, 10b>=46 ---> b>=4,6.. (no es entero, por lo tanto se aproxima al entero impar más cercano.. 5) b>4 Eso nos da como posibilidades para b=5,7 y 9. Luego, para b=5, es fácil ver que c>=5. Para cualquier otro valor de b, c puede tomar cualquier valor impar. Luego, es análogo para a=7, y a=9. Por lo tanto, se tiene que: 5555 5575 5595 5715 5735 5755 5775 5795 5915 5935 5955 5975 5995 7555 7575 7595 7715 7735 7755 7775 7795 7915 7935 7955 7975 7995 9555 9575 9595 9715 9735 9755 9775 9795 9915 9935 9955 9975 9995 Y sus respectivos negativos PD: Me equivoqué en esta.. pero meintras venía a la micro me di cuenta del cagaso, juajajaja Edit: Está mal!.. ..no da con c menor que 5.. Por lo tanto todas las soluciones que tengan "c" menor a 5, no da.. Mensaje modificado por GoChuck el Jun 12 2010, 11:59 AM |
|
|
|
 Jun 12 2010, 11:46 AM Jun 12 2010, 11:46 AM
Publicado:
#3
|
|
 Dios Matemático Supremo Grupo: Usuario FMAT Mensajes: 688 Registrado: 8-November 09 Desde: Villarrica Miembro Nº: 61.657 Nacionalidad:  Colegio/Liceo:  Universidad: .png) Sexo:  |
-------------------- yo no soy especial
a pesar que ella lo dijo tengo unos krk y un celular hechizo aún vácilo SFDK en el segundo piso y la frase final da igual la improviso |
|
|
|
 Jun 12 2010, 11:46 AM Jun 12 2010, 11:46 AM
Publicado:
#4
|
|
 Dios Matemático Supremo Grupo: Usuario FMAT Mensajes: 688 Registrado: 8-November 09 Desde: Villarrica Miembro Nº: 61.657 Nacionalidad:  Colegio/Liceo:  Universidad: .png) Sexo:  |
.
Mensaje modificado por Pedantic Anarchy el Jun 12 2010, 11:48 AM -------------------- yo no soy especial
a pesar que ella lo dijo tengo unos krk y un celular hechizo aún vácilo SFDK en el segundo piso y la frase final da igual la improviso |
|
|
|
 Jun 12 2010, 11:48 AM Jun 12 2010, 11:48 AM
Publicado:
#5
|
|
|
Dios Matemático Supremo Grupo: Usuario FMAT Mensajes: 2.847 Registrado: 3-October 09 Miembro Nº: 59.760 Nacionalidad:  Colegio/Liceo:  Universidad:  Sexo:  |
Hola te coopero con el 1) como es rectángulo el triangulo es mucho mas fácil
 |
|
|
|
 Jun 12 2010, 11:57 AM Jun 12 2010, 11:57 AM
Publicado:
#6
|
|
|
Dios Matemático Grupo: Usuario FMAT Mensajes: 400 Registrado: 27-October 09 Desde: ¡Qué te importa! Miembro Nº: 61.057 Universidad:  Sexo:  |
Bonitas soluciones
Acá va la mia. por pitágoras, se sabe que es rectángulo. Luego, como está inscrita debe ser tangente a sus lados. Por lo tanto, hay trazos iguales en lados diferentes. Por lo mismo, se llega a los sistemas de ecuaciones: x+z=8 x+y=15 z+y=17 resolviendo fácilmente, se llega a que x=3. Luego se trazan los radios perpendiculares a los lados (8 y 15), y nos quedaría un cuadrilátero con 3 ángulos rectos. Por lo tanto, el cuarto también debe serlo. Luego es un cuadrado o rectángulo. Y como dos lados perpendiculares miden lo mismo (en este caso lo dos radios, y los dos "x"), se sabe que es cuadrado. Luego el radio mide 3. Mensaje modificado por GoChuck el Jun 12 2010, 11:58 AM
Archivo(s) Adjunto(s)
|
|
|
|
 Jun 12 2010, 12:06 PM Jun 12 2010, 12:06 PM
Publicado:
#7
|
|
|
Dios Matemático Supremo Grupo: Usuario FMAT Mensajes: 9.897 Registrado: 6-April 08 Miembro Nº: 19.238 Nacionalidad:  Colegio/Liceo:  Sexo:  |
p2) Hay dos ciclistas ubicados a 60km de distancia. Estos avanzan con velocidades constantes de 10km/h, en sentidos opuestos. Una hábil e inteligente mosca, que vuela a 30km/h, va de ciclista en ciclista. Determine cuánto recorre la mosquita tssssssss lo que es el plagio ahhh ese problema esta en una de las primeras paginas del profe cesarator, lo titulo "la super mosca" voy a er si lo encuentro. apuesto a que ni nombraron la fuente. Mal po! lo encontre!!! na que verrrr! no me gusto. Mensaje modificado por Kaissa el Jun 12 2010, 12:10 PM -------------------- |
|
|
|
 Jun 12 2010, 12:10 PM Jun 12 2010, 12:10 PM
Publicado:
#8
|
|
|
Dios Matemático Grupo: Usuario FMAT Mensajes: 400 Registrado: 27-October 09 Desde: ¡Qué te importa! Miembro Nº: 61.057 Universidad:  Sexo:  |
Jajajajaja, puede ser
La verdad esque no veo el problema de poner el ejercicio.. En ninguna parte decían que era creado por ellos xD! Jajajaja.. A todo esto.. Kaissa, tú que eres bacana y seca.. me podís decir, qué parte del desarrollo del ejercicio 1 está malo? (o sea.. llegué a que con b>5, me servía cualquier c.. y no es así.. pero mi inecuación dice otra cosa Ah, y ese ejercicio lo encontré absurdamente fácil.. O puedo estar mal. p2) Es fácil darse cuenta que a las 3 horas se topan. Por lo tanto, la mosca vuela por un tiempo de 3 horas. Según los físicos, la distancia recorrida es igual al tiempo por la velocidad. Luego, la mosca recorre 3*30, y por lo tanto, 90km. |
|
|
|
 Jun 12 2010, 12:11 PM Jun 12 2010, 12:11 PM
Publicado:
#9
|
|
|
Dios Matemático Supremo Grupo: Usuario FMAT Mensajes: 9.897 Registrado: 6-April 08 Miembro Nº: 19.238 Nacionalidad:  Colegio/Liceo:  Sexo:  |
Para Poncelet usa que es rectangulo.
hay otra forma mas facil y bacanosa: r=2A/P A=area P=perimetro -------------------- |
|
|
|
 Jun 12 2010, 02:49 PM Jun 12 2010, 02:49 PM
Publicado:
#10
|
|
 Dios Matemático Supremo Grupo: Moderador Mensajes: 590 Registrado: 14-October 07 Miembro Nº: 11.310 Colegio/Liceo:  Universidad:  Sexo:  |
Problema 3: Sea 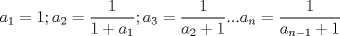 . Determine cuánto es : . Determine cuánto es : 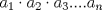 Bonita prueba, a mi juicio este estaba más entretenido y no es complejo: Asumiremos que el lector se maneja en lo que es la Sucesión de Fibonacci, definiremos esta sucesión como sigue:
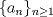 , podemos conjeturar que: , podemos conjeturar que: 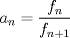 , la que probaremos por inducción. , la que probaremos por inducción.Esta proposición es cierta para 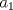 , asumiremos que lo es para , asumiremos que lo es para 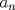 y probaremos que lo es para y probaremos que lo es para 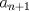 , por enunciado se tiene que: , por enunciado se tiene que: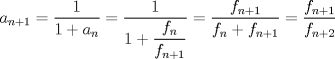 , ,esto último por definición de Fibonacci.  Luego el valor del producto del enunciado equivale a: 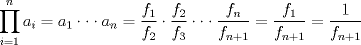 , ,Nos basta ver la sucesión de Fibonacci para hallar el valor respectivo y ya terminamos. PD: Para los más "jóvenes" en Olimpiadas sirve como un instructivo para que aprendan ciertas cosas útiles. Saludos y Dios los bendiga. Si quiere un aporte más vea esto: -------------------- |
|
|
|
  |
2 usuario(s) está(n) leyendo esta discusión (2 invitado(s) y 0 usuario(s) anónimo(s))
0 miembro(s):
| Versión Lo-Fi | Fecha y Hora actual: 3rd April 2025 - 09:28 PM |














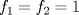 .
.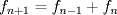 .
.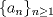 del problema es aún más estrecha, pues:
del problema es aún más estrecha, pues: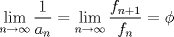 ,
,