I3 Álgebra y Geometría - Foro fmat.cl

Portal Matemático

¿Qué es FMAT?

Foro fmat.cl > Programa Enseñanza Universitaria > Comunidades Universitarias > Universidad Católica > Algebra

2 Páginas:

1 2 >

Reply to this topic

Start new topic

I3 Álgebra y Geometría, 1S 2010

Tela Ver Perfil del Miembro Ver los mensajes de este miembro	Jun 7 2010, 09:13 PM Publicado: #1
Dios Matemático Supremo Grupo: Colaborador Platinum Mensajes: 1.032 Registrado: 25-March 09 Desde: Quinta Normal Miembro Nº: 46.018 Nacionalidad: Colegio/Liceo: Universidad: Sexo:	$TEX: <br />\begin{center}<br />\noindent MAT1103 - Álgebra y Geometría\\<br />Interrogación 3\\<br />Su nota se calculará considerando sus mejores siete respuestas. \end{center}<br />\begin{enumerate}<br />\item Las raíces de $q(x) = 3x^3 -26x^2 +52x -24$ están en progresión geométrica. Encuéntrelas.<br />\item Encuentre las raíces del polinomio $x^3 -7x^2 +14x -20$, sabiendo que tiene una raíz compleja de módulo 2.<br />\item Demuestre que si a cada término de una progresión geométrica se le resta el siguiente, se forma otra progresión geométrica con la misma razón que la original.<br />\item Calcule el valor de $\displaystyle\sum_{k=1}^n \frac{k \cdot 3^k}{(k+3)!}$.<br />\item Demuestre que para $n \in \mathbb{N}$, $\displaystyle\sum_{k=1}^n k^2 \dbinom{n}{k} = n2^{n-1} + n(n-1)2^{n-2}$.<br />\item El juego del NIM consiste en una pila de fichas, de la que dos jugadores sacan, por turnos, entre una y tres fichas; el que saca la última ficha pierde.\\<br />Demuestre que la cantidad de fichas en la pila es múltiplo de 4, entonces el jugador de turno puede forzar la victoria.<br />\item Encuentre las ecuaciones de las rectas que pasan por el punto $(2,-3)$ y que están a distancia $3$ del punto $(1,2)$.<br />\item Demuestre que, dados dos vectores $\vec{u}$, $\vec{v} \in \mathbb{R}^n$, se cumple\\<br />$\|\|\vec{u} + \vec{v}\|\| = \|\|\vec{u} - \vec{v}\|\|$ si y sólo si $\vec{u} \perp \vec{v}$ .<br />\end{enumerate}<br />$ $TEX: Tiempo: 120 minutos$ $TEX: Sin Consultas$ $TEX: Sin calculadora$

Kura Ver Perfil del Miembro Ver los mensajes de este miembro	Jun 7 2010, 09:33 PM Publicado: #2
Dios Matemático Supremo Grupo: Usuario FMAT Mensajes: 1.918 Registrado: 14-May 08 Desde: The Tower of God Miembro Nº: 23.100 Nacionalidad: Colegio/Liceo: Universidad: Sexo:	Nose si estara bien: 8.- $TEX: $\\ \|\|u+v\|\| = \|\|u-v\|\| \\ \Leftrightarrow \sqrt{(u+v)^2} = \sqrt{(u-v)^2} \\ \Leftrightarrow \sqrt{u\cdot u + 2 u\cdot v + v\cdot v}= \sqrt{u\cdot u - 2u\cdot v + v\cdot v} \Leftrightarrow 2u \cdot v = -2u \cdot v \\ \Leftrightarrow u \cdot v = 0 \Leftrightarrow u \perp v $$ Mensaje modificado por Kura el Jun 7 2010, 09:39 PM -------------------- Far over... the misty mountains cold. To dungeons deep and caverns old. We must away ere break of day. To find our long-forgotten gold. The pines were roaring on the height. The winds were moaning in the night. The fire was red, it flaming spread. The trees like torches blazed with light. Apunte: Sistemas de Ecuaciones Cuadráticas! Apunte: Series de Fourier! Problemas Resueltos: EDO! OMG! Soy el ñoño de eléctrica.

Gastón Burrull	Jun 7 2010, 09:44 PM Publicado: #3
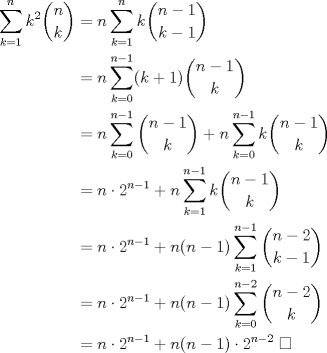Invitado	$TEX: \begin{align}<br />\sum_{k=1}^n k^2\dbinom{n}{k}&=n\sum_{k=1}^n k\dbinom{n-1}{k-1}\\<br />&=n\sum_{k=0}^{n-1} (k+1)\dbinom{n-1}{k}\\<br />&=n\sum_{k=0}^{n-1} \dbinom{n-1}{k}+n\sum_{k=0}^{n-1} k\dbinom{n-1}{k}\\<br />&=n\cdot 2^{n-1}+n\sum_{k=1}^{n-1} k\dbinom{n-1}{k}\\<br />&=n\cdot 2^{n-1}+n(n-1)\sum_{k=1}^{n-1} \dbinom{n-2}{k-1}\\<br />&=n\cdot 2^{n-1}+n(n-1)\sum_{k=0}^{n-2} \dbinom{n-2}{k}\\<br />&=n\cdot 2^{n-1}+n(n-1)\cdot 2^{n-2}\ \square<br />\end{align}$

Abu-Khalil Ver Perfil del Miembro Ver los mensajes de este miembro	Jun 7 2010, 10:13 PM Publicado: #4
Dios Matemático Supremo Grupo: Usuario FMAT Mensajes: 3.812 Registrado: 4-November 07 Desde: Santiago Miembro Nº: 12.213 Nacionalidad: Colegio/Liceo: Universidad: Sexo:	P4 $TEX: \[\sum_{k=1}^n\frac{k3^k}{(k+3)!}=\sum_{k=1}^n\frac{(k+3-3)3^k}{(k+3)!}=\sum_{k=1}^n\frac{3^k}{(k+2)!}-\sum_{k=1}^n\frac{3^{k+1}}{(k+3)!}=\frac{3}{3!}-\frac{3^{n+1}}{(n+3)!}.\]$ -------------------- ~milopez $TEX: \[\mathfrak{L}=\int_{-\infty}^\infty e^{-289x^2}dx=\frac{\Gamma (\frac{1}{2})}{17}=\frac{\sqrt{\pi}}{17}\]$ $TEX: <br />\begin{equation}\begin{aligned}<br />dS_t&=\mu S_t dt+\sqrt{V_t}S_t dW^S_t\\<br />dV_t&=\kappa(\theta-V_t)dt+\sigma\sqrt{V_t} dW^V_t\\<br />\end{aligned}\end{equation}<br />$ $TEX: <br />$$\mathbb A^{\text U}_M(N)$$<br />$

theraiden Ver Perfil del Miembro Ver los mensajes de este miembro	Jun 7 2010, 10:24 PM Publicado: #5
Principiante Matemático Grupo: Usuario FMAT Mensajes: 13 Registrado: 25-February 10 Miembro Nº: 66.131 Nacionalidad: Sexo:	comenze a resolver la 1) pero me dio lata xq muxo latex mira te dejo una img de un problema q resolvio un amigo que es muy parecido trata de ver que le puedes acer aqui te dejo la img prueba ver si te sirve

theraiden Ver Perfil del Miembro Ver los mensajes de este miembro	Jun 7 2010, 10:35 PM Publicado: #6
Principiante Matemático Grupo: Usuario FMAT Mensajes: 13 Registrado: 25-February 10 Miembro Nº: 66.131 Nacionalidad: Sexo:	no se si te sirva pero para el ejercicio n° 3 estableceremos la P.G de esta manera a1=2 a1=a2/q (q=razon) a2=6 a2=a2 a3=18 a3=a2q a4=54 a4=aq2 procedemos a restar el siguietnte 2-6=-4 6-18=-12 18-54=-36 entonces nuestra nueva P.G seria a1=-4 a2=-12 a3=-36 Recordemos que teniamos no se si te sirva pero para el ejercicio n° 3 estableceremos la P.G de esta manera a1=a2/q a2=a2 a3=a2q a4=aq2 remplazamos con el fin de obtener nuestra nueva q donde 1 nos daria al reemplazar a1 a2/q=-4 (a2=-12) q=-12/-4=3 por lo tanto nuestra q = 3 y si comprobamos nos da que si se pasa a aser una P.G espero serte de ayuda xq en realidad no c me ocurrio como hacerlo de otra forma

Kaissa Ver Perfil del Miembro Ver los mensajes de este miembro	Jun 8 2010, 11:38 AM Publicado: #7
Dios Matemático Supremo Grupo: Usuario FMAT Mensajes: 9.897 Registrado: 6-April 08 Miembro Nº: 19.238 Nacionalidad: Colegio/Liceo: Sexo:	$TEX: $ $\\<br />\textbf{Sp6}:\\<br />$ $\\<br />Podemos enunciar el problema de la siguiente forma:\\<br />$ $\\<br />Sea $n\in\mathbb{N}$, entonces si el NIM tiene $4n$ palitos, el jugador de turno puede forzar la victoria.\\<br />Procedemos por inducci\'on.\\<br />- Para $n=1$ es claramente cierta, pues si yo juego al principio puedo sacar tres palitos y mato a mi contrincante.\\<br />- Sea $k\in\mathbb{N}$ tal que para $4k$ palitos puedo matar a mi contrincante, entonces en la \'ultima jugada mi contrincante se ve en la obligaci\'on de sacar un palitos. Agregu\'emosle 4 palitos m\'as.\\<br />Si a\'un as\'i saca un palito en la \'ultima jugada, est\'a en problemas porque yo puedo sacar tres palitos y muere.\\<br />Si saca 2 palitos yo en el siguiente paso saco 2 y muere igual.\\<br />Si saca 3 palitos, yo en el siguiente paso saco 1 y muere.\\<br />Luego en cualquier caso mi contrincante muere.\\<br />De este modo he probado que con $4(k+1)$ palitos tambi\'en morir\'a.\\<br />Entonces el conjunto formado por los $n$ tales que con $4n$ palitos mi contrincante muere es inductivo<br />$ PD..... yo revisé antes de publicar, y funkaba bien. que raro se haya truncado despues mi mensaje.... en fin Mensaje modificado por Kaissa el Jun 8 2010, 01:28 PM -------------------- Este es un extracto de Qué es fmat by Kenshin. La pregunta para ti estimado(a) lector(a) es... ¿Qué haces tu para que ésto se cumpla?

Zev Ver Perfil del Miembro Ver los mensajes de este miembro	Jun 8 2010, 12:30 PM Publicado: #8
Maestro Matemático Grupo: Usuario FMAT Mensajes: 97 Registrado: 26-January 10 Miembro Nº: 65.423 Nacionalidad: Universidad: Sexo:	como que te falto el [/tex] -------------------- ------------------------- CITA(El Geek @ Jul 10 2010, 09:59 PM) este ejercicio se puede resolver fácimente con PSU, ¿Ruffini? ¿Fermant? (nah que ver xD) ¿Ceva? ¿Pico? digo, Pitot, NO SEÑOR NO, las pelotas esos viejos ahora! Me va a dar un infarto

Zev Ver Perfil del Miembro Ver los mensajes de este miembro	Jun 8 2010, 02:48 PM Publicado: #9
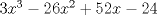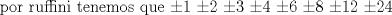Maestro Matemático Grupo: Usuario FMAT Mensajes: 97 Registrado: 26-January 10 Miembro Nº: 65.423 Nacionalidad: Universidad: Sexo:	$TEX: intentare hacer el 1... 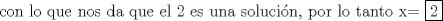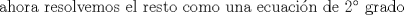aclaro que no soy universitario y me meti aca de puro copuchento, si lo hize mal o si cometi errores acepto insultos xd$ $TEX: $3x^3-26x^2+52x-24$$ $TEX: por ruffini tenemos que $\pm 1$ $\pm 2$ $\pm 3$ $\pm 4$ $\pm 6$ $\pm 8$ $\pm 12$ $\pm 24$$ $TEX: probamos con el 2$ $TEX: con lo que nos da que el 2 es una solución, por lo tanto x= $\boxed{2}$$ $TEX: ahora resolvemos el resto como una ecuación de 2° grado$ $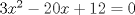TEX: $3x^2-20x+12=0$$ $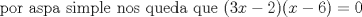TEX: por aspa simple nos queda que $(3x-2)(x-6)=0$$ $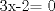TEX: 3x-2= 0$ $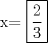TEX: x= $\boxed{\dfrac{2}{3}}$$ $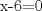TEX: x-6=0$ $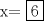TEX: x= $\boxed{6}$$ $TEX: teniendo las 3 raices podemos deducir que el factor de progresión es el 3$ -------------------- ------------------------- CITA(El Geek @ Jul 10 2010, 09:59 PM) este ejercicio se puede resolver fácimente con PSU, ¿Ruffini? ¿Fermant? (nah que ver xD) ¿Ceva? ¿Pico? digo, Pitot, NO SEÑOR NO, las pelotas esos viejos ahora! Me va a dar un infarto

ErnestoJ Ver Perfil del Miembro Ver los mensajes de este miembro	Feb 3 2014, 01:23 PM Publicado: #10
Principiante Matemático Grupo: Usuario FMAT Mensajes: 12 Registrado: 6-October 13 Miembro Nº: 123.055 Nacionalidad: Colegio/Liceo: Universidad: Sexo:	CITA(Gastón Burrull @ Jun 7 2010, 09:44 PM) $TEX: \begin{align}<br />\sum_{k=1}^n k^2\dbinom{n}{k}&=n\sum_{k=1}^n k\dbinom{n-1}{k-1}\\<br />&=n\sum_{k=0}^{n-1} (k+1)\dbinom{n-1}{k}\\<br />&=n\sum_{k=0}^{n-1} \dbinom{n-1}{k}+n\sum_{k=0}^{n-1} k\dbinom{n-1}{k}\\<br />&=n\cdot 2^{n-1}+n\sum_{k=1}^{n-1} k\dbinom{n-1}{k}\\<br />&=n\cdot 2^{n-1}+n(n-1)\sum_{k=1}^{n-1} \dbinom{n-2}{k-1}\\<br />&=n\cdot 2^{n-1}+n(n-1)\sum_{k=0}^{n-2} \dbinom{n-2}{k}\\<br />&=n\cdot 2^{n-1}+n(n-1)\cdot 2^{n-2}\ \square<br />\end{align}$ Por favor, explícame cómo y por qué, en la línea 3, en la segunda suma tienes k = 0 ; y en la línea 4 es k = 1. ¿Cuál es el principio en que se basa ese cambio? Mensaje modificado por ErnestoJ el Feb 3 2014, 01:38 PM

« Posterior · Algebra · Anterior »

2 Páginas:

1 2 >

Reply to this topic

Start new topic

1 usuario(s) está(n) leyendo esta discusión (1 invitado(s) y 0 usuario(s) anónimo(s))

0 miembro(s):

Modo de Ver: Estándar · Cambiar a: Lineal+ · Cambiar a: Outline

Suscribirse · Enviar por correo · Imprimir · Suscribirse a este foro

Versión Lo-Fi

Fecha y Hora actual: 3rd April 2025 - 04:22 PM

Powered By IP.Board 2.2.1 © 2007 IPS, Inc.