 Sólo para los fmat-eros de verdad, Primera Maratón Mayor de FMAT |
|
|
|
|
|
|
  |
 Feb 23 2011, 07:44 PM
Publicado:
#51
|
|
 Maestro Matemático  Grupo: Usuario FMAT Mensajes: 107 Registrado: 29-October 07 Desde: San Felipe-Santiago Miembro Nº: 11.941 Nacionalidad:  Universidad:  Sexo:   |
CITA(coquitao @ Feb 23 2011, 07:34 PM)  Si a y b son dos puntos distintos de M entonces sea f una aplicación continua de M a los reales tal que f(a) = 0 y f(b) = 1. Al ser M conexo y f continua se tiene que f(M) es un conexo de los reales que contiene a 0 y a 1 (y por tanto contiene al intervalo [0,1]). Se cumple así que el cardinal de M es mayor o igual al cardinal de f(M), que a su vez es mayor o igual al cardinal de [0,1] y la prueba termina. P.D. Por cierto, me tocaba proponer a mi. Bien, esta sí es una respuesta. Una forma similar era considerar f: M--->R dada por: f(u)=d(a,u) y considerar a,b distintos y ambos en M. Propuse para darle un up al tema. Salu2 |
 |
 
|
|
Feb 23 2011, 08:20 PM
Publicado:
#52
|
|
|
Dios Matemático Supremo Grupo: Usuario FMAT Mensajes: 2.818 Registrado: 3-October 09 Miembro Nº: 59.773 Nacionalidad: Colegio/Liceo:  Universidad:  Sexo:  |
El que le dio UP fue otra persona... sensual y adorable como yo
-------------------- Me voy, me jui.
|
|
|
|
|
Feb 23 2011, 11:03 PM
Publicado:
#53
|
|
|
Dios Matemático Supremo  Grupo: Super Moderador Mensajes: 2.065 Registrado: 25-May 08 Desde: Pelotillehue Miembro Nº: 24.463 |
CITA(galois @ Feb 23 2011, 06:44 PM) Propuse para darle un up al tema. De acuerdo... Mi comentario era parte en broma. Supongo entonces que ahora sí me toca proponer. XD -------------------- "Please forget everything you have learned in school; for you haven't learned it... Please keep in mind at all times the corresponding portions of your school curriculum; for you haven't actually forgotten them." -- E. Landau
|
|
|
|
|
Apr 17 2011, 08:14 PM
Publicado:
#54
|
|
 Dios Matemático Supremo Grupo: Usuario FMAT Mensajes: 765 Registrado: 6-December 05 Miembro Nº: 458 Nacionalidad: Sexo: |
Se ve interesante esto. ¿Van a seguir o no?
Saludos -------------------- Pasten, un buen muchacho en quien confiar.
|
|
|
|
|
Apr 17 2011, 08:38 PM
Publicado:
#55
|
|
|
Dios Matemático Supremo Grupo: Usuario FMAT Mensajes: 2.818 Registrado: 3-October 09 Miembro Nº: 59.773 Nacionalidad: Colegio/Liceo: Universidad: Sexo: |
Pastén tirándole palos a Coquitao. Eso en mi casa es velorio.
Uyui 
Mensaje modificado por El Geek el Apr 17 2011, 08:41 PM -------------------- Me voy, me jui.
|
|
|
|
 Sep 5 2011, 10:34 PM
Publicado:
#56
|
|
|
Dios Matemático Supremo Grupo: Usuario FMAT Mensajes: 558 Registrado: 11-April 10 Desde: Santiago Miembro Nº: 68.358 Nacionalidad: Colegio/Liceo:  Universidad:  Sexo: |
Y el propuesto de Coquitao??
.. En todo caso y muy Off Topic , veo la mayoría sólo respuestas de Coquitao. Quizás faltan contendientes como Pasten, Jorgeston, Krizalid, Kenshin, Kaissa... nose, varios mas Hasta ahora va ganando Coquitao |
|
|
|
|
Sep 13 2011, 01:24 AM
Publicado:
#57
|
|
|
Dios Matemático Supremo Grupo: Super Moderador Mensajes: 2.065 Registrado: 25-May 08 Desde: Pelotillehue Miembro Nº: 24.463 |
Uno simple: determine (con demostración) el grupo de Galois de la extensión
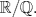
-------------------- "Please forget everything you have learned in school; for you haven't learned it... Please keep in mind at all times the corresponding portions of your school curriculum; for you haven't actually forgotten them." -- E. Landau
|
|
|
|
|
May 14 2012, 01:16 PM
Publicado:
#58
|
|
|
Dios Matemático Supremo Grupo: Usuario FMAT Mensajes: 765 Registrado: 6-December 05 Miembro Nº: 458 Nacionalidad: Sexo: |
Hola
yo respondi esto pero en otro tema dentro del foro. Eso cuenta? propongo? -------------------- Pasten, un buen muchacho en quien confiar.
|
|
|
|
|
Aug 19 2012, 09:23 PM
Publicado:
#59
|
|
|
Dios Matemático Supremo Grupo: Super Moderador Mensajes: 2.065 Registrado: 25-May 08 Desde: Pelotillehue Miembro Nº: 24.463 |
CITA(Pasten @ May 14 2012, 12:16 PM) Hola. Yo respondí esto pero en otro tema dentro del foro. ¿Eso cuenta? ¿Propongo? Adelante... -------------------- "Please forget everything you have learned in school; for you haven't learned it... Please keep in mind at all times the corresponding portions of your school curriculum; for you haven't actually forgotten them." -- E. Landau
|
|
|
|
|
Aug 20 2012, 12:24 AM
Publicado:
#60
|
|
|
Dios Matemático Supremo Grupo: Usuario FMAT Mensajes: 765 Registrado: 6-December 05 Miembro Nº: 458 Nacionalidad: Sexo: |
CITA(coquitao @ Aug 19 2012, 10:23 PM) Adelante... Si un entero N es un cuadrado modulo m para todos los modulos enteros m>0, es necesariamente verdad que N es un cuadrado en los enteros? ----- Me informan por interno que alguna vez ya pregunte algo similar en el foro. Si este problema es muy facil para usted, entonces diga algo interesante sobre el siguiente problema mas general: Sea P un polinomio con coeficientes enteros y sea N un entero. Suponga que para todo modulo entero m>0 existe un entero k tal que P(k) es congruente a N modulo m (o sea, supongamos que N esta en la imagen de P modulo m siempre). Es verdad que existe un entero K tal que P(K)=N? El problema para cuadrados es simplemente el caso P(x)=x^2. Mensaje modificado por Pasten el Aug 20 2012, 12:09 PM -------------------- Pasten, un buen muchacho en quien confiar.
|
|
|
|
|
1 usuario(s) está(n) leyendo esta discusión (1 invitado(s) y 0 usuario(s) anónimo(s))
0 miembro(s):
| Versión Lo-Fi | Fecha y Hora actual: 23rd November 2024 - 05:17 PM |
