|
|
|
|
|
|
|
  |
 Jun 1 2010, 05:51 PM Jun 1 2010, 05:51 PM
Publicado:
#31
|
|
 Dios Matemático Supremo Grupo: Usuario FMAT Mensajes: 1.564 Registrado: 12-November 07 Desde: La Union, XIV Region de los Rios Miembro Nº: 12.607 Nacionalidad:  Colegio/Liceo:  Universidad:  Sexo:  |
Sí es posible. 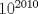 es el primer número con 2011 dígitos. Luego, si c(k) denota la cantidad de números con k dígitos se sigue que es el primer número con 2011 dígitos. Luego, si c(k) denota la cantidad de números con k dígitos se sigue que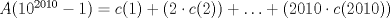 Claramente, los c(k)'s son fáciles de obtener explícitamente. ∎ Humm... es posible obtener explícitamente c(k) pero aun asi, calcular explicitamente A(n) a partir de c(k) no es tan directo. Por ejemplo, a simple vista $1/n$ se ve "nice" pero calcular 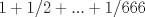 no es tan nice. no es tan nice.Creo que mejor debi haber pedido calcular explicitamente 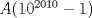 (Lo cual no es dificil de generalizar). Lamento los inconvenientes, la resp es correcta pero como no fue tan emocionante, le aumente un poquito la dificultad. (Lo cual no es dificil de generalizar). Lamento los inconvenientes, la resp es correcta pero como no fue tan emocionante, le aumente un poquito la dificultad.
-------------------- Ricardo Vargas Obando
Ex-alumno Deutsche Schule La Unión (Generación 2010, de los 150 años). Novato de Licenciatura en Matemática/Estadística, en la Pontificia Universidad Católica de Chile.  Grupo de facebook de Novatos Matemática y Estadística PUC 2011 Currículum Olímpico:
|
|
|
|
 Jun 1 2010, 06:42 PM Jun 1 2010, 06:42 PM
Publicado:
#32
|
|
|
Dios Matemático Supremo Grupo: Super Moderador Mensajes: 2.065 Registrado: 25-May 08 Desde: Pelotillehue Miembro Nº: 24.463 |
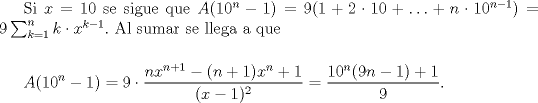
-------------------- "Please forget everything you have learned in school; for you haven't learned it... Please keep in mind at all times the corresponding portions of your school curriculum; for you haven't actually forgotten them." -- E. Landau
|
|
|
|
 Jun 1 2010, 06:49 PM Jun 1 2010, 06:49 PM
Publicado:
#33
|
|
 Dios Matemático Supremo Grupo: Usuario FMAT Mensajes: 1.564 Registrado: 12-November 07 Desde: La Union, XIV Region de los Rios Miembro Nº: 12.607 Nacionalidad:  Colegio/Liceo:  Universidad:  Sexo:  |
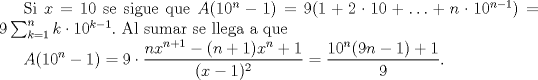 Sip, esa era la idea del problema. Ojo, la idea medular era notar que 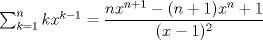 , y esta suma se puede probar ocupando el hecho que , y esta suma se puede probar ocupando el hecho que  inteligentemente. inteligentemente.Sin nada más que agregar, doy por resuelto el problema. Atentos con el de coquitao ^^ -------------------- Ricardo Vargas Obando
Ex-alumno Deutsche Schule La Unión (Generación 2010, de los 150 años). Novato de Licenciatura en Matemática/Estadística, en la Pontificia Universidad Católica de Chile.  Grupo de facebook de Novatos Matemática y Estadística PUC 2011 Currículum Olímpico:
|
|
|
|
 Jun 1 2010, 10:05 PM Jun 1 2010, 10:05 PM
Publicado:
#34
|
|
|
Dios Matemático Supremo Grupo: Super Moderador Mensajes: 2.065 Registrado: 25-May 08 Desde: Pelotillehue Miembro Nº: 24.463 |
4. Sea
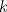 un natural mayor que un natural mayor que 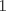 y y 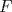 un elemento de un elemento de ![TEX: $\mathbb{Z}[x_{1}, \ldots, x_{k}].$](./tex/794064d900a2fe40f89c70dd12a9b263.png) Demuestre o refute lo siguiente: Demuestre o refute lo siguiente: 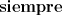 es posible hallar un es posible hallar un 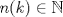 y y ![TEX: $f_{1}, \ldots, f_{n(k)} \in \mathbb{Z}[x]$](./tex/6da50bb809a8f33a638dfea3fc0db5f7.png) tales que tales que 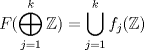 . .Uno de mi cosecha. 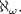
-------------------- "Please forget everything you have learned in school; for you haven't learned it... Please keep in mind at all times the corresponding portions of your school curriculum; for you haven't actually forgotten them." -- E. Landau
|
|
|
|
 Jun 4 2010, 05:36 PM Jun 4 2010, 05:36 PM
Publicado:
#35
|
|
|
Dios Matemático Supremo Grupo: Super Moderador Mensajes: 2.065 Registrado: 25-May 08 Desde: Pelotillehue Miembro Nº: 24.463 |
Upeando, por si acaso no lo habían visto... Una manera equivalente de formular la pregunta es:
4. Sea 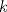 un natural mayor que un natural mayor que 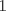 y y 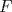 un elemento de un elemento de ![TEX: $\mathbb{Z}[x_{1}, \ldots, x_{k}].$](./tex/794064d900a2fe40f89c70dd12a9b263.png) Demuestre o refute lo siguiente: Demuestre o refute lo siguiente: 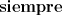 es posible hallar un es posible hallar un 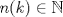 y y ![TEX: $f_{1}, \ldots, f_{n(k)} \in \mathbb{Z}[x]$](./tex/0aa201b97736c998f43c0ba4ff28f372.png) tales que tales que 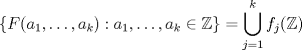 . .
-------------------- "Please forget everything you have learned in school; for you haven't learned it... Please keep in mind at all times the corresponding portions of your school curriculum; for you haven't actually forgotten them." -- E. Landau
|
|
|
|
 Jun 4 2010, 06:10 PM Jun 4 2010, 06:10 PM
Publicado:
#36
|
|
|
Dios Matemático Supremo Grupo: Usuario FMAT Mensajes: 2.818 Registrado: 3-October 09 Miembro Nº: 59.773 Nacionalidad:  Colegio/Liceo:  Universidad:  Sexo:  |
.
Mensaje modificado por El Geek el Feb 21 2011, 03:17 PM -------------------- Me voy, me jui.
|
|
|
|
 Jun 9 2010, 10:36 PM Jun 9 2010, 10:36 PM
Publicado:
#37
|
|
|
Dios Matemático Supremo Grupo: Super Moderador Mensajes: 2.065 Registrado: 25-May 08 Desde: Pelotillehue Miembro Nº: 24.463 |
La hora del relevo:
4. Calcule la siguiente suma 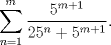 Se espera, claramente, que el resultado aparezca reducido a su mínima expresión. -------------------- "Please forget everything you have learned in school; for you haven't learned it... Please keep in mind at all times the corresponding portions of your school curriculum; for you haven't actually forgotten them." -- E. Landau
|
|
|
|
 Jun 12 2010, 11:19 PM Jun 12 2010, 11:19 PM
Publicado:
#38
|
|
 Dios Matemático Supremo Grupo: Moderador Mensajes: 590 Registrado: 14-October 07 Miembro Nº: 11.310 Colegio/Liceo:  Universidad:  Sexo:  |
La hora del relevo: 4. Calcule la siguiente suma 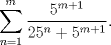 Se espera, claramente, que el resultado aparezca reducido a su mínima expresión. Dividiremos el problema en dos casos: Que m sea par o impar.
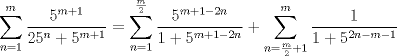 (*). (*).Luego note que si asociamos el primer término de la de la primera sumatoria del segundo miembro de (*) con el último de la segunda sumatoria del mismo miembro, el segundo de la primera sumatoria con el penúltimo de la segunda sumatoria y así sucesivamente tenemos que la suma equivale a: 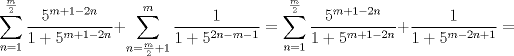 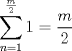 . .
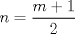 , por lo que éste será igual a: , por lo que éste será igual a: 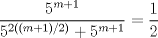 , y como todos los demás términos apareados tienen suma igual a , y como todos los demás términos apareados tienen suma igual a 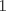 , tenemos que la suma equivale a: , tenemos que la suma equivale a: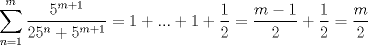 . .Y con esto finalizamos. Saludos colega coquitao y se espera su pronta revisión A mi juicio mucho más fácil que el anterior, por lo menos en notación, esperamos tu apreciación en esto coquitao. -------------------- |
|
|
|
 Jun 13 2010, 09:51 AM Jun 13 2010, 09:51 AM
Publicado:
#39
|
|
|
Dios Matemático Supremo Grupo: Super Moderador Mensajes: 2.065 Registrado: 25-May 08 Desde: Pelotillehue Miembro Nº: 24.463 |
Buena, makmat. Sólo era cosa de explotar la simetría inherente al propuesto. En cuanto al nivel de dificultad hay dos observaciones importantes que hacer:
1) Se publicaron dos versiones del problema anterior. La segunda versión explicaba, implícitamente, la notación usada en la formulación original del propuesto. Luego, no es muy exacto decir que la dificultad de dicho problema era consecuencia exclusiva de los símbolos raros presentes en él. 2) Efectivamente, el propuesto es un tanto más fácil que el anterior. Sin embargo, el que haya recibido solución después de andar tres días en el aire me hace tener serias dudas al respecto. Eso sería. Se espera ansiosamente tu propuesto, makmat. -------------------- "Please forget everything you have learned in school; for you haven't learned it... Please keep in mind at all times the corresponding portions of your school curriculum; for you haven't actually forgotten them." -- E. Landau
|
|
|
|
 Jun 13 2010, 11:59 AM Jun 13 2010, 11:59 AM
Publicado:
#40
|
|
 Dios Matemático Supremo Grupo: Moderador Mensajes: 590 Registrado: 14-October 07 Miembro Nº: 11.310 Colegio/Liceo:  Universidad:  Sexo:  |
Luego de la revisión de mi colega coquitao, no ralentizaré más esta Maratón y aquí va el Problema 5, que a mi juicio es instructivo para quienes recién incursionan en Topología.
5. Sea 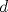 la métrica usual y la métrica usual y 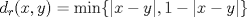 , ambas distancias definidas en , ambas distancias definidas en 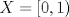 . .Decida la continuidad de la función 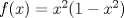 , considerada como: , considerada como:
Con respecto a que el propuesto anterior fue respondido en 3 días, yo creo que porque nadie se animaba a postearlo no porque faltaran capacidades, yo lo ví ayer y al ratito salió, y creánme que yo sé que no faltan Fmat-eros que hubieran respondido el propuesto, sólo faltaba animarse, así que les infundo ánimo para este propuesto. -------------------- |
|
|
|
  |
1 usuario(s) está(n) leyendo esta discusión (1 invitado(s) y 0 usuario(s) anónimo(s))
0 miembro(s):
| Versión Lo-Fi | Fecha y Hora actual: 3rd April 2025 - 08:56 PM |












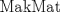
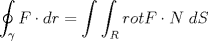
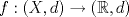 .
.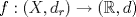 .
.