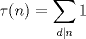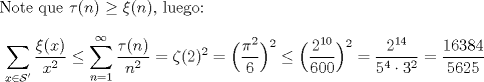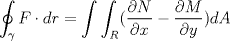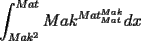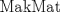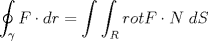|
|
|
|
|
|
|
  |
 Jun 3 2010, 03:26 PM Jun 3 2010, 03:26 PM
Publicado:
#91
|
|
 Dios Matemático Supremo Grupo: Usuario FMAT Mensajes: 1.564 Registrado: 12-November 07 Desde: La Union, XIV Region de los Rios Miembro Nº: 12.607 Nacionalidad:  Colegio/Liceo:  Universidad:  Sexo:  |
no caxe, como llegas a la 2da igualdad de tu solucion (la q tiene pi) o es algo conocido xd Es un hecho "conocido" que 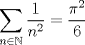 No quisiera entrometerme demasiado, pero creo que no puede haber una solución más directa que esa. Fatal, you are the MAN! Por favor, entreguénle de una vez los premios al Sr. Jajaj gracias por los elogios coquitao Saludos y a la espera del veredicto de makmat -------------------- Ricardo Vargas Obando
Ex-alumno Deutsche Schule La Unión (Generación 2010, de los 150 años). Novato de Licenciatura en Matemática/Estadística, en la Pontificia Universidad Católica de Chile.  Grupo de facebook de Novatos Matemática y Estadística PUC 2011 Currículum Olímpico:
|
|
|
|
 Jun 3 2010, 05:44 PM Jun 3 2010, 05:44 PM
Publicado:
#92
|
|
 Dios Matemático Supremo Grupo: Moderador Mensajes: 590 Registrado: 14-October 07 Miembro Nº: 11.310 Colegio/Liceo:  Universidad:  Sexo:  |
 Sinceramente no me parecio muy olimpica este intento de solución, espero que tu solución si sea olimpica. pd: 16384/5625... que numero mas "deprimente" xD Correcto, pero lo de "deprimente" no era necesario porque por lo menos en mi solución sí tiene su encanto. No quisiera entrometerme demasiado, pero creo que no puede haber una solución más directa que esa. Fatal, you are the MAN! Por favor, entreguénle de una vez los premios al Sr. La verdad... de directa no sé si esta sea la "más", la mía anda por ahí... y yo creo que la mía si tiene "pinta" Olímpica, a decir verdad, vi un problema de una Olimpiada de Europa que usaba esta clase de conocimientos, pero no salía de lo Olímpico. Os muestro mi solución: De verdad mucho más Olímpica, pero eso queda a su criterio. -------------------- |
|
|
|
 Jun 3 2010, 06:21 PM Jun 3 2010, 06:21 PM
Publicado:
#93
|
|
 Dios Matemático Supremo Grupo: Usuario FMAT Mensajes: 1.564 Registrado: 12-November 07 Desde: La Union, XIV Region de los Rios Miembro Nº: 12.607 Nacionalidad:  Colegio/Liceo:  Universidad:  Sexo:  |
Sigamos con un problema apto para todo público, hay al menos dos soluciones (donde se admiten varios variantes), asi que el camino no es único.

-------------------- Ricardo Vargas Obando
Ex-alumno Deutsche Schule La Unión (Generación 2010, de los 150 años). Novato de Licenciatura en Matemática/Estadística, en la Pontificia Universidad Católica de Chile.  Grupo de facebook de Novatos Matemática y Estadística PUC 2011 Currículum Olímpico:
|
|
|
|
 Jun 3 2010, 07:37 PM Jun 3 2010, 07:37 PM
Publicado:
#94
|
|
 Dios Matemático Supremo Grupo: Usuario FMAT Mensajes: 532 Registrado: 19-October 08 Desde: Santa Cruz de la Sierra Miembro Nº: 36.531 Nacionalidad:  Sexo:  |
Aqui mi solucion:
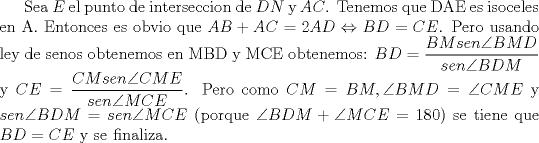 Sorry por no poner dibujo -------------------- "I've never let my school interfere with my education.”
|
|
|
|
 Jun 3 2010, 07:54 PM Jun 3 2010, 07:54 PM
Publicado:
#95
|
|
 Dios Matemático Supremo Grupo: Usuario FMAT Mensajes: 1.564 Registrado: 12-November 07 Desde: La Union, XIV Region de los Rios Miembro Nº: 12.607 Nacionalidad:  Colegio/Liceo:  Universidad:  Sexo:  |
Aqui mi solucion:  Sorry por no poner dibujo Solo un mínimo error de tipeo, pero la idea es correcta Este problemita era simple, no hay que tenerle miedo. Dispare el siguiente Diego -------------------- Ricardo Vargas Obando
Ex-alumno Deutsche Schule La Unión (Generación 2010, de los 150 años). Novato de Licenciatura en Matemática/Estadística, en la Pontificia Universidad Católica de Chile.  Grupo de facebook de Novatos Matemática y Estadística PUC 2011 Currículum Olímpico:
|
|
|
|
 Jun 3 2010, 08:39 PM Jun 3 2010, 08:39 PM
Publicado:
#96
|
|
 Dios Matemático Supremo Grupo: Usuario FMAT Mensajes: 532 Registrado: 19-October 08 Desde: Santa Cruz de la Sierra Miembro Nº: 36.531 Nacionalidad:  Sexo:  |
El sgt problema me lo invente yo haciendo otro problema de geometria, la parte a) esta facil y la b) ya se complica un poco.
  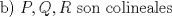 -------------------- "I've never let my school interfere with my education.”
|
|
|
|
 Jun 4 2010, 12:38 AM Jun 4 2010, 12:38 AM
Publicado:
#97
|
|
|
Dios Matemático Supremo Grupo: Super Moderador Mensajes: 2.065 Registrado: 25-May 08 Desde: Pelotillehue Miembro Nº: 24.463 |
Os muestro mi solución: Ir a http://www.fmat.cl/index.php?showtopic=516...t=0#entry369733 para una prueba de la identidad central en el enfoque de makmat. -------------------- "Please forget everything you have learned in school; for you haven't learned it... Please keep in mind at all times the corresponding portions of your school curriculum; for you haven't actually forgotten them." -- E. Landau
|
|
|
|
 Jun 4 2010, 10:46 PM Jun 4 2010, 10:46 PM
Publicado:
#98
|
|
 Matemático Grupo: Usuario FMAT Mensajes: 45 Registrado: 20-October 07 Miembro Nº: 11.559 Nacionalidad:  Sexo:  |
  Mensaje modificado por Assassin.... el Jul 8 2010, 01:02 PM |
|
|
|
 Jun 5 2010, 12:46 PM Jun 5 2010, 12:46 PM
Publicado:
#99
|
|
 Dios Matemático Supremo Grupo: Usuario FMAT Mensajes: 532 Registrado: 19-October 08 Desde: Santa Cruz de la Sierra Miembro Nº: 36.531 Nacionalidad:  Sexo:  |
Excelente solucion, la idea de usar pascal no se me habia ocurrido, pero de todas formas lo habia desmotrado usando complejos (luego pongo la solucion, que es bastante cortita ^^). dispare su problema
-------------------- "I've never let my school interfere with my education.”
|
|
|
|
 Jun 5 2010, 01:29 PM Jun 5 2010, 01:29 PM
Publicado:
#100
|
|
 Matemático Grupo: Usuario FMAT Mensajes: 45 Registrado: 20-October 07 Miembro Nº: 11.559 Nacionalidad:  Sexo:  |
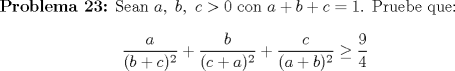
|
|
|
|
  |
1 usuario(s) está(n) leyendo esta discusión (1 invitado(s) y 0 usuario(s) anónimo(s))
0 miembro(s):
| Versión Lo-Fi | Fecha y Hora actual: 2nd April 2025 - 08:51 PM |










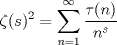
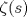 es la función Zeta de Riemann y
es la función Zeta de Riemann y