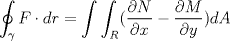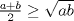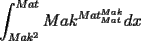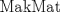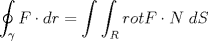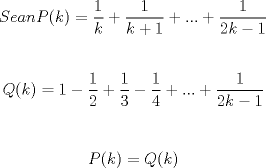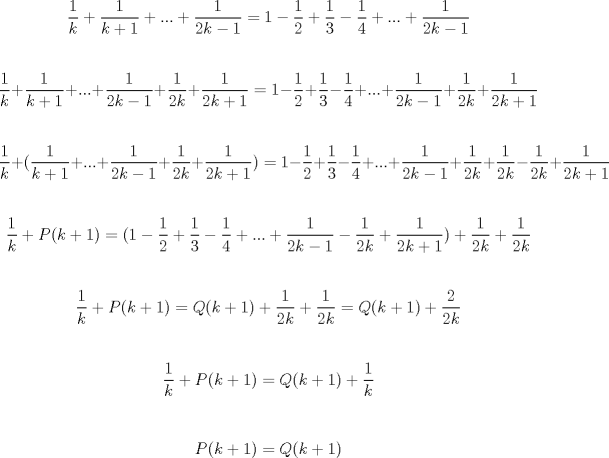|
|
|
|
|
|
|
  |
 May 5 2010, 05:24 PM May 5 2010, 05:24 PM
Publicado:
#11
|
|
 Dios Matemático Supremo Grupo: Usuario FMAT Mensajes: 532 Registrado: 19-October 08 Desde: Santa Cruz de la Sierra Miembro Nº: 36.531 Nacionalidad:  Sexo:  |
pondre otro hint pues el problema ya lleva mucho tiempo:
-------------------- "I've never let my school interfere with my education.”
|
|
|
|
 May 5 2010, 08:11 PM May 5 2010, 08:11 PM
Publicado:
#12
|
|
 Dios Matemático Supremo Grupo: Moderador Mensajes: 590 Registrado: 14-October 07 Miembro Nº: 11.310 Colegio/Liceo:  Universidad:  Sexo:  |
Matemos el problema de una vez... (lo intenté, pero el último hint fue la clave)
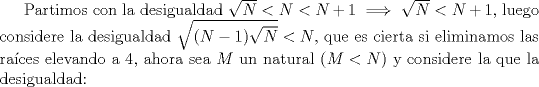 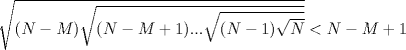  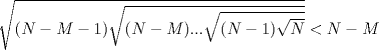 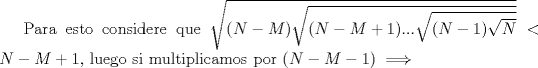 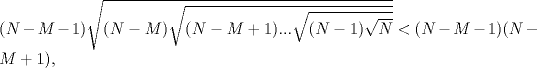 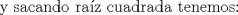 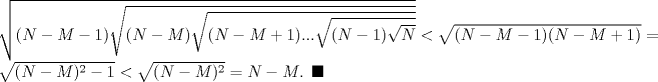 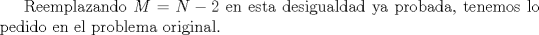 Simplemente hermoso... un tipo raro de inducción, pero al final salió Propondré el siguiente si está correcto. Saludos y Dios los bendiga. PD: diego me siento realizado -------------------- |
|
|
|
 May 5 2010, 08:57 PM May 5 2010, 08:57 PM
Publicado:
#13
|
|
 Dios Matemático Supremo Grupo: Usuario FMAT Mensajes: 532 Registrado: 19-October 08 Desde: Santa Cruz de la Sierra Miembro Nº: 36.531 Nacionalidad:  Sexo:  |
Solucion correcta, amigo Makkmat, al final valio la pena tanto cabezeo.
-------------------- "I've never let my school interfere with my education.”
|
|
|
|
 May 5 2010, 10:44 PM May 5 2010, 10:44 PM
Publicado:
#14
|
|
 Dios Matemático Supremo Grupo: Moderador Mensajes: 590 Registrado: 14-October 07 Miembro Nº: 11.310 Colegio/Liceo:  Universidad:  Sexo:  |
No sabía que problema colocar, al principio iba a colocar uno asesino xd, pero me arrepentí pues servirá para la Futura Maratón 2010, así que ahí va uno no tan compejo:
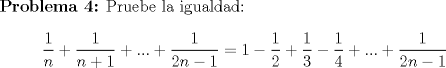 Saludos y intentenlo que no es difícil, ni parecido con el problema 3 que "casi" arruinó la Maratón. Sin hints por ahora. -------------------- |
|
|
|
 May 6 2010, 08:47 AM May 6 2010, 08:47 AM
Publicado:
#15
|
|
 Dios Matemático Supremo Grupo: Usuario FMAT Mensajes: 1.564 Registrado: 12-November 07 Desde: La Union, XIV Region de los Rios Miembro Nº: 12.607 Nacionalidad:  Colegio/Liceo:  Universidad:  Sexo:  |
No olviden que es sólo para estudiantes de media, secundaria pero no universitarios ni graduados porfa D: Por eso eliminé la respuesta correcta que se había colocado.
Como estoy en clases, me remito a decir un par de comentarios del p3. Como se vió, la clave era el segundo hint dado por el buen Diego (a partir de ahí era "sencillo", pero sin ese hint se veía mucho más complicado). De hecho, al ver el hint, había llegado a la misma respuesta que makmat, y la estaba escribiendo pero...ya saben el resto El p4 es bien bonito y no es difícil. Saludos! -------------------- Ricardo Vargas Obando
Ex-alumno Deutsche Schule La Unión (Generación 2010, de los 150 años). Novato de Licenciatura en Matemática/Estadística, en la Pontificia Universidad Católica de Chile.  Grupo de facebook de Novatos Matemática y Estadística PUC 2011 Currículum Olímpico:
|
|
|
|
 May 6 2010, 05:14 PM May 6 2010, 05:14 PM
Publicado:
#16
|
|
 Dios Matemático Supremo Grupo: Team Ensayos FMAT Mensajes: 1.559 Registrado: 18-November 07 Miembro Nº: 12.754 Nacionalidad:  Sexo:  |
|
|
|
|
 May 6 2010, 05:16 PM May 6 2010, 05:16 PM
Publicado:
#17
|
|
|
Dios Matemático Supremo Grupo: Usuario FMAT Mensajes: 1.429 Registrado: 6-October 07 Miembro Nº: 10.987 |
Solo queria comentar que la Solucion a ese problema de makmat creo que involucra usar Telescopicas y esas cosas, y esa solucion por Induccion no se me habia ocurrido, ademas q lo encuentro muy engorroso xdd.
Eso era :x -------------------- CHAO.
|
|
|
|
 May 6 2010, 05:24 PM May 6 2010, 05:24 PM
Publicado:
#18
|
|
 Dios Matemático Supremo Grupo: Team Ensayos FMAT Mensajes: 1.559 Registrado: 18-November 07 Miembro Nº: 12.754 Nacionalidad:  Sexo:  |
Solo queria comentar que la Solucion a ese problema de makmat creo que involucra usar Telescopicas y esas cosas, y esa solucion por Induccion no se me habia ocurrido, ademas q lo encuentro muy engorroso xdd. Eso era :x que pesao ehm...telescopicas la verdad lo aprendi el año pasado por m icuenta y nunca hice problemasde eso, asi que lo tengo medio olvidado...y lo de engorroso, casi todas las soluciones de iduccion que he visto salen enmas de 3 lineas XD y por cierto...no creo que un problema tenga "una" solucion, como tu nombras que la de telescopicas es La Solucion del problema, aunque me pareceria bonito ver la de telescopicas,a ver si mañanalo repaso y la saco Saludos! Mensaje modificado por Hamon el May 6 2010, 05:25 PM -------------------- Empezando con Desigualdades? Encuentra aquí problemas resueltos
|
|
|
|
 May 6 2010, 05:26 PM May 6 2010, 05:26 PM
Publicado:
#19
|
|
|
Dios Matemático Supremo Grupo: Usuario FMAT Mensajes: 1.429 Registrado: 6-October 07 Miembro Nº: 10.987 |
que pesao ehm...telescopicas la verdad lo aprendi el año pasado por m icuenta y nunca hice problemasde eso, asi que lo tengo medio olvidado...y lo de engorroso, casi todas las soluciones de iduccion que he visto salen enmas de 3 lineas XD Saludos! Ahahaha no fue de pesao, es q creo q habia visto este problema y la Solucion involucraba esas cosas, y a mi como Opinion Personal no me gusta Induccion, lo encuentro engorrosos no se xd. PD: Dejemos de desvirtuar :x -------------------- CHAO.
|
|
|
|
 May 6 2010, 07:04 PM May 6 2010, 07:04 PM
Publicado:
#20
|
|
|
Dios Matemático Supremo Grupo: Super Moderador Mensajes: 2.065 Registrado: 25-May 08 Desde: Pelotillehue Miembro Nº: 24.463 |
Lo que ocurre aquí es que inducción es sólo una herramienta para verificar la validez de la cosas. Una prueba con ese método no da, por lo general, información adicional de por qué motivo las cosas funcionan como funcionan.
Ojalá Fatal haya respaldado la respuesta de anoche pues era considerablemente más corta e intuitiva que la que se ha publicado hoy. Sobra decir que la idea de la prueba aquella no radicaba en el uso de sumas telescópicas o de inducción. Consistía solamente en expresar de dos modos distintos una misma cantidad, igualar y QED. -------------------- "Please forget everything you have learned in school; for you haven't learned it... Please keep in mind at all times the corresponding portions of your school curriculum; for you haven't actually forgotten them." -- E. Landau
|
|
|
|
  |
1 usuario(s) está(n) leyendo esta discusión (1 invitado(s) y 0 usuario(s) anónimo(s))
0 miembro(s):
| Versión Lo-Fi | Fecha y Hora actual: 8th July 2025 - 12:48 AM |






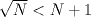 con N entero, tomen en cuenta el anterior hint tambien
con N entero, tomen en cuenta el anterior hint tambien