|
|
|
|
|
|
|
  |
 Apr 13 2010, 08:30 PM Apr 13 2010, 08:30 PM
Publicado:
#1
|
|
 Dios Matemático Supremo Grupo: Colaborador Platinum Mensajes: 1.032 Registrado: 25-March 09 Desde: Quinta Normal Miembro Nº: 46.018 Nacionalidad:  Colegio/Liceo:  Universidad:  Sexo:  |
![TEX: <br />\begin{center}<br />\noindent MAT1103 - Álgebra y Geometría\\<br />Control 1 - Martes 13 de Abril de 2010 \end{center}<br />\textbf{Fila A}<br />\begin{enumerate}<br />\item Resuelva la inecuación<br />\[2\left|x\right|+\left|x-4\right|-7 > 2 \sqrt{ 2(x-5)(x+2) }.\]<br />\item Demuestre que la función<br />\[f(x)=x^3-5x-\dfrac{2}{x}\]<br />es creciente en [1,+$\infty$).<br /><br />\textbf{Ayuda:} Use el hecho que si $a,b>0$, entonces $a^2 +b^2 > 2ab.$<br />\end{enumerate}<br />](./tex/c855f0c2869eeca1adf8018c48c324bf.png) ![TEX: <br />\textbf{Fila B}<br />\begin{enumerate}<br />\item Resuelva la inecuación<br />\[2\left|x\right|+\left|x-3\right|-3 > 2 \sqrt{ 2(x-3)(x+1) }.\]<br />\item Demuestre que la función<br />\[f(x)=x^3-4x-\dfrac{1}{x}\]<br />es creciente en [1,+$\infty$).<br /><br />\textbf{Ayuda:} Use el hecho que si $a,b>0$, entonces $a^2 +b^2 > 2ab.$<br />\end{enumerate}<br />](./tex/3d244266f423b1a18a50c761978efe50.png) 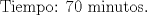 |
|
|
|
 Apr 13 2010, 08:42 PM Apr 13 2010, 08:42 PM
Publicado:
#2
|
|
 Dios Matemático Supremo Grupo: Usuario FMAT Mensajes: 1.832 Registrado: 26-October 07 Desde: concepción Miembro Nº: 11.853 Nacionalidad:  Colegio/Liceo:  Universidad:  Sexo:  |
yo tengo una duda,siendo que tengo este ramo pero aún no vamos en esa materia... es "valido" usar concepto de derivada para el ejercicio 2 ?
-------------------- -la inteligencia no es un privilegio, sino un don en benefio de los hermanos...
-un gran don conlleva una gran responzabilidad... -un libro puede saber más que un estudiante, pero es mejor el estudiante, ya que el estudiante es capaz de razonar y pensar (fuera de lo espiritual que también es importante)... Paz y Bien...=) |
|
|
|
 Apr 13 2010, 08:47 PM Apr 13 2010, 08:47 PM
Publicado:
#3
|
|
 Dios Matemático Supremo Grupo: Usuario FMAT Mensajes: 3.812 Registrado: 4-November 07 Desde: Santiago Miembro Nº: 12.213 Nacionalidad:  Colegio/Liceo:  Universidad:  Sexo:  |
yo tengo una duda,siendo que tengo este ramo pero aún no vamos en esa materia... es "valido" usar concepto de derivada para el ejercicio 2 ? No. -------------------- |
|
|
|
 Apr 14 2010, 10:02 PM Apr 14 2010, 10:02 PM
Publicado:
#4
|
|
 Dios Matemático Supremo Grupo: Team Ensayos FMAT Mensajes: 1.294 Registrado: 16-March 09 Desde: ancud Miembro Nº: 45.100 Nacionalidad:  Colegio/Liceo:  Universidad:  Sexo:  |
1. Fila A
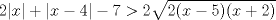 Primero restringimos ![TEX: $R: (x-5)(x+2)\ge 0$ $\Rightarrow R:(-\infty,-2]\cup[5,\infty+)$](./tex/36358e395c375d9ee5ea6d8ccae44211.png) 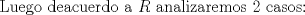 ![TEX: $C_1:x\in(-\infty,-2]$](./tex/11cb9f6cc01c58931f7e9acc28394846.png) 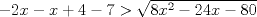 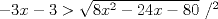 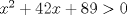 ![TEX: luego $x=-21+-4\sqrt{22}$ $\Rightarrow S_{pC_1}=(-\infty,-21-4\sqrt{22}]\cup[-2+4\sqrt{22},\infty+)$](./tex/fb1acab83430c4a23f26ecdc13bdc079.png) ![TEX: $S_{fC_1}=(-\infty,-21-4\sqrt{22}]\cup[-2+4\sqrt{22},-2]$](./tex/2542a9f4d09a7735f165ec98f882080f.png) 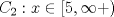 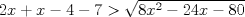 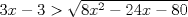 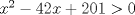 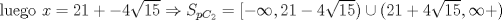 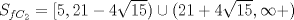 ![TEX: $S=(-\infty,-21-4\sqrt{22}]\cup[-2+4\sqrt{22},-2]\cup[5,21-4\sqrt{15})\cup(21+4\sqrt{15},\infty+)$](./tex/3e421703a7a1faf77c6bb2a1715abbfe.png) Debo decir que bastante feo el problemaaa x(! mas de alguna vez tube que recurrir a mi calculadoraa para verificar resultados xdd saludos --------------------   Estudiante de 4° año ing civil mec utfsm |
|
|
|
 Apr 15 2010, 06:29 AM Apr 15 2010, 06:29 AM
Publicado:
#5
|
|
 Dios Matemático Supremo Grupo: Colaborador Platinum Mensajes: 1.032 Registrado: 25-March 09 Desde: Quinta Normal Miembro Nº: 46.018 Nacionalidad:  Colegio/Liceo:  Universidad:  Sexo:  |
|
|
|
|
 Apr 15 2010, 07:31 PM Apr 15 2010, 07:31 PM
Publicado:
#6
|
|
 Dios Matemático Supremo Grupo: Usuario FMAT Mensajes: 3.812 Registrado: 4-November 07 Desde: Santiago Miembro Nº: 12.213 Nacionalidad:  Colegio/Liceo:  Universidad:  Sexo:  |
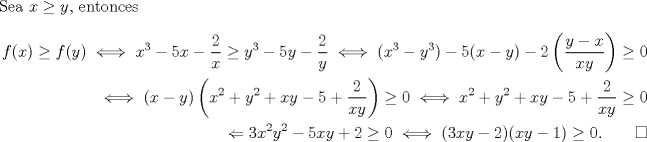
-------------------- |
|
|
|
 Apr 16 2010, 07:33 AM Apr 16 2010, 07:33 AM
Publicado:
#7
|
|
 Dios Matemático Supremo Grupo: Colaborador Platinum Mensajes: 1.032 Registrado: 25-March 09 Desde: Quinta Normal Miembro Nº: 46.018 Nacionalidad:  Colegio/Liceo:  Universidad:  Sexo:  |
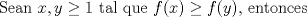 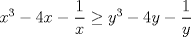 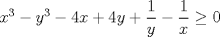 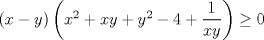 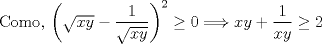 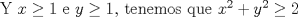 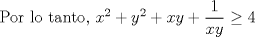 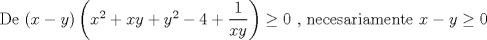 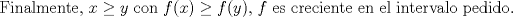
|
|
|
|
 Jan 10 2014, 06:14 PM Jan 10 2014, 06:14 PM
Publicado:
#8
|
|
|
Principiante Matemático Grupo: Usuario FMAT Mensajes: 12 Registrado: 6-October 13 Miembro Nº: 123.055 Nacionalidad:  Colegio/Liceo:  Universidad:  Sexo:  |
|
|
|
|
 Jan 10 2014, 07:05 PM Jan 10 2014, 07:05 PM
Publicado:
#9
|
|
 Dios Matemático Grupo: Usuario FMAT Mensajes: 321 Registrado: 25-February 13 Miembro Nº: 115.593 Nacionalidad:  Universidad:  Sexo:  |
|
|
|
|
 Jan 10 2014, 08:06 PM Jan 10 2014, 08:06 PM
Publicado:
#10
|
|
 Dios Matemático Supremo Grupo: Usuario FMAT Mensajes: 3.812 Registrado: 4-November 07 Desde: Santiago Miembro Nº: 12.213 Nacionalidad:  Colegio/Liceo:  Universidad:  Sexo:  |
¿Cómo rayos pasaste de la antepenúltima expresión a la penúltima? Usé la ayuda que te daban. -------------------- |
|
|
|
  |
1 usuario(s) está(n) leyendo esta discusión (1 invitado(s) y 0 usuario(s) anónimo(s))
0 miembro(s):
| Versión Lo-Fi | Fecha y Hora actual: 3rd April 2025 - 04:24 PM |











![TEX: \[\mathfrak{L}=\int_{-\infty}^\infty e^{-289x^2}dx=\frac{\Gamma (\frac{1}{2})}{17}=\frac{\sqrt{\pi}}{17}\]](./tex/e0e88dba678ca3ead120b088f41191b2.png)


![TEX: $\sqrt[3]{\dfrac{1}{\cos\left(\frac{\pi}{7}\right)}}-\sqrt[3]{\dfrac{1}{\cos\left(\frac{2\pi}{7}\right)}}+\sqrt[3]{\dfrac{1}{\cos\left(\frac{3\pi}{7}\right)}}=\sqrt[3]{6\sqrt[3]{7}-8}$](./tex/c5b49cf6584e89b12a82db6b29f2cd73.png)

