|
|
|
|
|
|
|
  |
 Apr 9 2010, 07:53 PM Apr 9 2010, 07:53 PM
Publicado:
#1
|
|
 Dios Matemático Supremo Grupo: Usuario FMAT Mensajes: 858 Registrado: 20-August 09 Desde: In my House Miembro Nº: 57.323 Nacionalidad:  Colegio/Liceo:  Universidad:  Sexo:  |
6ª OLIMPIADA INTERNACIONAL DE MATEMÁTICA Moscow, Rusia, 1964 Primera Prueba: Problema 1: (a) Encuentre todos los enteros positivos  para lo cuál para lo cuál 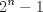 es divisible por 7 es divisible por 7(b) Pruebe que no hay enteros positivos  para lo cuál para lo cuál  es divisible por 7. es divisible por 7.Problema 2: Suponga que 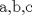 son los lados de un triángulo. Pruebe que son los lados de un triángulo. Pruebe que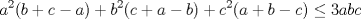 Problema 3: El incírculo es inscrito en un triángulo 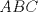 de lados de lados 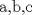 . Tres tangentes al círculo son paralelas a los lados del . Tres tangentes al círculo son paralelas a los lados del 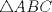 . Estas tangentes forman tres pequeños triángulos (al interior de . Estas tangentes forman tres pequeños triángulos (al interior de 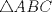 ). Determine la suma de las áreas de los cuatro incírculos (en términos de ). Determine la suma de las áreas de los cuatro incírculos (en términos de 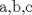 ). ).Segunda Prueba: Problema 4: Diecisiete estudiantes hablan con todos los demás estudiantes. Todos ellos hablan acerca de tres temas diferentes. Cada pareja de estudiantes hablan de un tema. Pruebe que existen tres estudiantes que hablan del mismo tema entre ellos. Problema 5: Se dan 5 puntos en un plano. Entre las líneas que unen estos cinco puntos, no hay dos ni que coincidan, ni que sean paralelas ni perpendiculares. A través de cada punto se construyen las alturas de cada una de las otras líneas. ¿Cuál es el número máximo de intersecciones de estas alturas (excluyendo los cinco puntos)? Problema 6: Dado un tetraedro 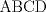 , sea , sea 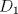 el centroide del triángulo el centroide del triángulo 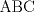 , y sean , y sean 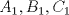 los puntos de intersección de las líneas paralelas a los puntos de intersección de las líneas paralelas a 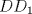 y que pasan a través de y que pasan a través de 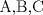 con las caras opuestas del tetraedro. Pruebe que el volúmen del tetraedro con las caras opuestas del tetraedro. Pruebe que el volúmen del tetraedro 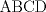 es un tercio del volúmen del tetraedro es un tercio del volúmen del tetraedro 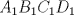 . ¿El resultado sigue siendo verdadero si se reemplaza . ¿El resultado sigue siendo verdadero si se reemplaza 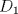 con álgun punto del triángulo con álgun punto del triángulo 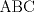 ? ?Resumen de soluciones Mensaje modificado por EnemyOfGod286 el Apr 9 2010, 07:55 PM |
|
|
|
 Apr 9 2010, 08:03 PM Apr 9 2010, 08:03 PM
Publicado:
#2
|
|
 Dios Matemático Supremo Grupo: Usuario FMAT Mensajes: 858 Registrado: 20-August 09 Desde: In my House Miembro Nº: 57.323 Nacionalidad:  Colegio/Liceo:  Universidad:  Sexo:  |
P1 (a) Vemos que
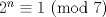 . Notemos que para cualquier valor de . Notemos que para cualquier valor de 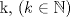 , , 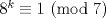 . .Por lo que todos los  que cumplan con lo pedido son los de la forma que cumplan con lo pedido son los de la forma 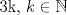 . .(b) Sea 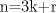 , donde , donde 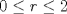 . Luego la expresión nos queda: . Luego la expresión nos queda: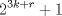 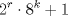 . Aplicando modulo 7. . Aplicando modulo 7.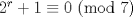 Por lo que 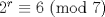 Viendo los tres casos 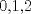 . No existe ningún . No existe ningún  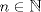 tal que tal que  sea divisible por 7. sea divisible por 7.
Mensaje modificado por EnemyOfGod286 el Apr 9 2010, 08:12 PM |
|
|
|
 Apr 11 2010, 02:21 PM Apr 11 2010, 02:21 PM
Publicado:
#3
|
|
 Dios Matemático Grupo: Usuario FMAT Mensajes: 234 Registrado: 5-April 10 Desde: Arg Miembro Nº: 67.793 Nacionalidad:  Sexo:  |
Por que el P1 es re facil si es una IMO?, podria estar en un provincial en argentina! me imagino que regalaron menciones
--------------------  |
|
|
|
 Apr 11 2010, 06:41 PM Apr 11 2010, 06:41 PM
Publicado:
#4
|
|
 Dios Matemático Supremo Grupo: Usuario FMAT Mensajes: 1.564 Registrado: 12-November 07 Desde: La Union, XIV Region de los Rios Miembro Nº: 12.607 Nacionalidad:  Colegio/Liceo:  Universidad:  Sexo:  |
Problema 2: Suponga que 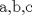 son los lados de un triángulo. Pruebe que son los lados de un triángulo. Pruebe que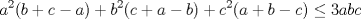  Por que el P1 es re facil si es una IMO?, podria estar en un provincial en argentina! me imagino que regalaron menciones Ver para creer Comentp ahora la solucion de Enemy: * Cuando notas felizmente que 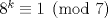 , no puedes concluir inmediatamente que TODOS los n que cumplen lo pedido son los de la forma , no puedes concluir inmediatamente que TODOS los n que cumplen lo pedido son los de la forma 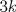 . Lo ùnico que hiciste fue comprobar que los de la forma . Lo ùnico que hiciste fue comprobar que los de la forma 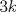 cumplen lo pedido pero no descartaste el resto. cumplen lo pedido pero no descartaste el resto. Arregla ese inconveniente, y ya se estaría listo el P1 (aunque quizás falta algún nexo conector que conecte tus últimas 2 frases para facilitar la comprensión). -------------------- Ricardo Vargas Obando
Ex-alumno Deutsche Schule La Unión (Generación 2010, de los 150 años). Novato de Licenciatura en Matemática/Estadística, en la Pontificia Universidad Católica de Chile.  Grupo de facebook de Novatos Matemática y Estadística PUC 2011 Currículum Olímpico:
|
|
|
|
 Apr 11 2010, 08:56 PM Apr 11 2010, 08:56 PM
Publicado:
#5
|
|
 Dios Matemático Supremo Grupo: Moderador Mensajes: 590 Registrado: 14-October 07 Miembro Nº: 11.310 Colegio/Liceo:  Universidad:  Sexo:  |
CITA(EnemyOfGod286 @ Apr 9 2010, 09:53 PM) Problema 4: Diecisiete estudiantes hablan con todos los demás estudiantes. Todos ellos hablan acerca de tres temas diferentes. Cada pareja de estudiantes hablan de un tema. Pruebe que existen tres estudiantes que hablan del mismo tema entre ellos.    Saludos -------------------- |
|
|
|
 Apr 11 2010, 09:11 PM Apr 11 2010, 09:11 PM
Publicado:
#6
|
|
 Dios Matemático Supremo Grupo: Usuario FMAT Mensajes: 858 Registrado: 20-August 09 Desde: In my House Miembro Nº: 57.323 Nacionalidad:  Colegio/Liceo:  Universidad:  Sexo:  |
|
|
|
|
 Apr 12 2010, 02:38 PM Apr 12 2010, 02:38 PM
Publicado:
#7
|
|
 Dios Matemático Grupo: Usuario FMAT Mensajes: 234 Registrado: 5-April 10 Desde: Arg Miembro Nº: 67.793 Nacionalidad:  Sexo:  |
Debe ser que en el momento no eran my usuales los problemas que salian con algebra modular
--------------------  |
|
|
|
 May 19 2010, 11:57 PM May 19 2010, 11:57 PM
Publicado:
#8
|
|
|
Principiante Matemático Grupo: Usuario FMAT Mensajes: 7 Registrado: 19-December 08 Miembro Nº: 41.015 Nacionalidad:  Colegio/Liceo:  Universidad:  Sexo:  |
Mensaje modificado por Hernan27 el May 20 2010, 08:45 PM |
|
|
|
 Jan 18 2015, 11:58 AM Jan 18 2015, 11:58 AM
Publicado:
#9
|
|
 Dios Matemático Supremo Grupo: Usuario FMAT Mensajes: 783 Registrado: 23-April 13 Desde: Constitución Miembro Nº: 118.027 Nacionalidad:  Universidad:  Sexo:  |
P2
--------------------    |
|
|
|
 Jan 18 2015, 01:15 PM Jan 18 2015, 01:15 PM
Publicado:
#10
|
|
|
Doctor en Matemáticas Grupo: Usuario FMAT Mensajes: 192 Registrado: 23-August 10 Miembro Nº: 75.906 Nacionalidad:  Colegio/Liceo:  Sexo:  |
Desarrollamos, obtenemos que tenemos que probar que :
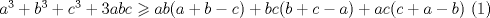 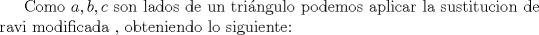  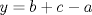 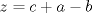 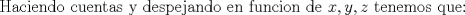 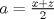 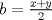 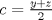 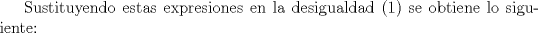 ![TEX: $ \frac{1}{8}[ (x+y)^3+(y+z)^3+(z+y)^3]\geq \frac{1}{4}[ (x+y)(x+z)x+(x+y)(y+z)y+(x+z)(y+z)z ] $](/tex-image/6b2963151eef0799b24481efea70f408.png) 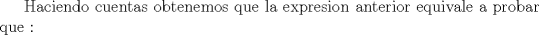 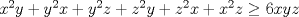  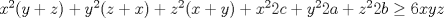 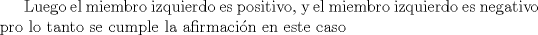
Mensaje modificado por nagernager el Jan 18 2015, 03:15 PM |
|
|
|
  |
2 usuario(s) está(n) leyendo esta discusión (2 invitado(s) y 0 usuario(s) anónimo(s))
0 miembro(s):
| Versión Lo-Fi | Fecha y Hora actual: 3rd April 2025 - 08:53 PM |












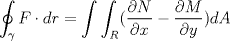

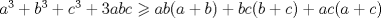 (1)
(1)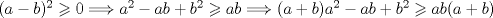
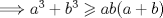
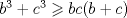
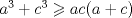
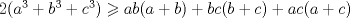 (2)
(2)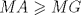 se sabe que
se sabe que