I3 Variable Compleja - Foro fmat.cl

Portal Matemático

¿Qué es FMAT?

Foro fmat.cl > Programa Enseñanza Universitaria > Comunidades Universitarias > Universidad Católica > Variable Compleja

Reply to this topic

Start new topic

I3 Variable Compleja, 2s 2009

DressedToKill Ver Perfil del Miembro Ver los mensajes de este miembro	Apr 1 2010, 02:35 PM Publicado: #1
Dios Matemático Supremo Grupo: Usuario FMAT Mensajes: 1.818 Registrado: 21-December 06 Miembro Nº: 3.434	Prof. Alejando Ramirez $TEX: \noindent<br />\begin{enumerate}<br />\item[(1)] Sea $f$ una función analítica en el disco $\Delta$ de centro $0$ y radio $R$. Supongamos que para alguna constante $M > 0$ se tiene que $\|f(z)\| \le M$ para todo $z \in \Delta$ y que para algún natural $n \ge 1$ tenemos<br />$$0 = f(0) = f'(0) = \cdots = f^{(n)}(0).$$<br />Demuestre que<br />$$\|f(z)\| \le M \left(\dfrac{\|z\|}{R} \right)^{n+1},$$<br />para todo $z \in \Delta$, con igualdad si y sólo si existe un $\alpha$ tal que $\|\alpha\| = 1$ y $f(z) = \alpha M \left(\frac{z}{R}\right)^{n+1}$ para todo $z \in \Delta$.<br />\item[(2)] Demuestre que todo mapeo conforme $1-1$ desde un disco sobre otro está dado por una transformación lineal fraccionaria.<br />\item[(3)] Encuentre el número de raíces que tiene el polinomio $z^7-2z^5+6z^3-z+1$ en el disco $\|z\| < 1$.<br />\item[(4)] Ocupando el método de los residuos calcule la integral<br />$$\displaystyle\int_0^{\infty} {\dfrac{x \sin(x)}{x^2+a^2}} dx, a > 0$$<br />\end{enumerate}<br />$ -------------------- http://www.youtube.com/watch?v=sp_WV91jx8E...feature=related

Abu-Khalil Ver Perfil del Miembro Ver los mensajes de este miembro	Nov 9 2010, 09:22 PM Publicado: #2
Dios Matemático Supremo Grupo: Usuario FMAT Mensajes: 3.812 Registrado: 4-November 07 Desde: Santiago Miembro Nº: 12.213 Nacionalidad: Colegio/Liceo: Universidad: Sexo:	P3 $TEX: \noindent Usaremos el Teorema de Rouché. Notemos que para $\|z\|=1$<br />\[\left\|(z^7-2z^5+6z^3-z+1)-6z^3\right\|\le \left\|z^7\right\|+2\left\|z^5\right\|+\left\|z\right\|+\left\|1\right\|=5<6=\left\|6z^3\right\|.\]<br />Por lo tanto, como $z^3$ tiene a $0$ como raíz con multiplicidad 3, concluimos que $z^7-2z^5+6z^3-z+1$ tiene tres raíces en el disco unitario.<br />$ P4 $TEX: \noindent Sea <br />\[f(z)=\frac{ze^{iz}}{z^2+a^2}.\]<br />Integraremos sobre la semicircuferencia superior de radio $R>0$. Sean $\gamma_1(t)=t$ para $-R\le t\le R$ y $\gamma_2(\theta)=Re^{i\theta}$ para $0\le \theta\le\pi$. Entonces si $\gamma=\gamma_1\cup\gamma_2$ tenemos que<br />\[\int_{\gamma_1}f(z)dz+\int_{\gamma_2}f(z)dz=\oint_\gamma f(z)dz=2\pi i\operatorname{Res}(f,ia),\]<br />Por otro lado, <br />\begin{equation}\begin{aligned}<br />\left\|\int_{\gamma_2}f(z)dz\right\|&=\left\|\int_0^{\pi}\frac{Re^{i\theta}e^{iRe^{i\theta}}}{R^2e^{i2\theta}+a^2}iRe^{i\theta}d\theta\right\|\le\int_0^\pi\left\|\frac{iR^2}{R^2e^{i2\theta}+a^2}\right\|<br />\left\|e^{iRe^{i\theta}}\right\|\left\|e^{i2\theta}\right\|d\theta\\<br />&\le \frac{R^2}{R^2-a^2}\int_0^\pi \left\|e^{iR(\cos\theta+i\sin\theta)}\right\|d\theta\le\frac{R^2}{R^2-a^2}\int_0^\pi e^{-R\sin\theta}d\theta.<br />\end{aligned}\end{equation}<br />Luego, cuando $R\to\infty$, como el integrando y el intervalo está acotado, usamos el Teorema de Convergencia Dominada de Lebesgue y sigue que<br />\[\lim_{R\to\infty}\left\|\int_{\gamma_2}f(z)dz\right\|=\lim_{R\to\infty}\frac{R^2}{R^2-a^2}\int_0^\pi e^{-R\sin\theta}d\theta=\int_0^\pi \lim_{R\to\infty}e^{-R\sin\theta}d\theta=0.\]<br />Además, como $f$ tiene un polo simple en $z=ia$, tenemos que<br />\[\operatorname{Res}(f,ia)=\lim_{z\to ia}(z-ia)f(z)=\lim_{z\to ia}(z-ia)\frac{ze^{iz}}{z^2+a^2}=\lim_{z\to ia}\frac{ze^{iz}}{z+ia}=\frac{e^{-a}}{2}.\]<br />Por lo tanto,<br />\[\int_{\gamma_1}f(z)dz=i\pi e^{-a}.\]<br />Pero <br />\[\int_{\gamma_1}f(z)dz=\int_{-\infty}^{\infty}\frac{xe^{ix}}{x^2+a^2}=\int_{-\infty}^{\infty}\frac{x\cos x}{x^2+a^2}dx+i\int_{-\infty}^{\infty}\frac{x\sin x}{x^2+a^2}dx.\]<br />Así, igualando parte imaginaria con parte imaginaria y aprovechandonos de la paridad de la función, concluimos que<br />\[\int_{0}^{\infty}\frac{x\sin x}{x^2+a^2}dx=\frac{1}{2}\int_{-\infty}^{\infty}\frac{x\sin x}{x^2+a^2}dx=\frac{\pi}{2}e^{-a}.\]<br />$ -------------------- ~milopez $TEX: \[\mathfrak{L}=\int_{-\infty}^\infty e^{-289x^2}dx=\frac{\Gamma (\frac{1}{2})}{17}=\frac{\sqrt{\pi}}{17}\]$ $TEX: <br />\begin{equation}\begin{aligned}<br />dS_t&=\mu S_t dt+\sqrt{V_t}S_t dW^S_t\\<br />dV_t&=\kappa(\theta-V_t)dt+\sigma\sqrt{V_t} dW^V_t\\<br />\end{aligned}\end{equation}<br />$ $TEX: <br />$$\mathbb A^{\text U}_M(N)$$<br />$

The Number of Th... The Number of The Beast Ver Perfil del Miembro Ver los mensajes de este miembro	Aug 29 2011, 02:36 PM Publicado: #3
Dios Matemático Supremo Grupo: Usuario FMAT Mensajes: 691 Registrado: 22-April 09 Miembro Nº: 49.114 Nacionalidad: Colegio/Liceo: Sexo:	CITA(Abu-Khalil @ Nov 9 2010, 10:22 PM) P3 $TEX: \noindent Usaremos el Teorema de Rouché. Notemos que para $\|z\|=1$<br />\[\left\|(z^7-2z^5+6z^3-z+1)-6z^3\right\|\le \left\|z^7\right\|+2\left\|z^5\right\|+\left\|z\right\|+\left\|1\right\|=5<6=\left\|6z^3\right\|.\]<br />Por lo tanto, como $z^3$ tiene a $0$ como raíz con multiplicidad 3, concluimos que $z^7-2z^5+6z^3-z+1$ tiene tres raíces en el disco unitario.<br />$ P4 $TEX: \noindent Sea <br />\[f(z)=\frac{ze^{iz}}{z^2+a^2}.\]<br />Integraremos sobre la semicircuferencia superior de radio $R>0$. Sean $\gamma_1(t)=t$ para $-R\le t\le R$ y $\gamma_2(\theta)=Re^{i\theta}$ para $0\le \theta\le\pi$. Entonces si $\gamma=\gamma_1\cup\gamma_2$ tenemos que<br />\[\int_{\gamma_1}f(z)dz+\int_{\gamma_2}f(z)dz=\oint_\gamma f(z)dz=2\pi i\operatorname{Res}(f,ia),\]<br />Por otro lado, <br />\begin{equation}\begin{aligned}<br />\left\|\int_{\gamma_2}f(z)dz\right\|&=\left\|\int_0^{\pi}\frac{Re^{i\theta}e^{iRe^{i\theta}}}{R^2e^{i2\theta}+a^2}iRe^{i\theta}d\theta\right\|\le\int_0^\pi\left\|\frac{iR^2}{R^2e^{i2\theta}+a^2}\right\|<br />\left\|e^{iRe^{i\theta}}\right\|\left\|e^{i2\theta}\right\|d\theta\\<br />&\le \frac{R^2}{R^2-a^2}\int_0^\pi \left\|e^{iR(\cos\theta+i\sin\theta)}\right\|d\theta\le\frac{R^2}{R^2-a^2}\int_0^\pi e^{-R\sin\theta}d\theta.<br />\end{aligned}\end{equation}<br />Luego, cuando $R\to\infty$, como el integrando y el intervalo está acotado, usamos el Teorema de Convergencia Dominada de Lebesgue y sigue que<br />\[\lim_{R\to\infty}\left\|\int_{\gamma_2}f(z)dz\right\|=\lim_{R\to\infty}\frac{R^2}{R^2-a^2}\int_0^\pi e^{-R\sin\theta}d\theta=\int_0^\pi \lim_{R\to\infty}e^{-R\sin\theta}d\theta=0.\]<br />Además, como $f$ tiene un polo simple en $z=ia$, tenemos que<br />\[\operatorname{Res}(f,ia)=\lim_{z\to ia}(z-ia)f(z)=\lim_{z\to ia}(z-ia)\frac{ze^{iz}}{z^2+a^2}=\lim_{z\to ia}\frac{ze^{iz}}{z+ia}=\frac{e^{-a}}{2}.\]<br />Por lo tanto,<br />\[\int_{\gamma_1}f(z)dz=i\pi e^{-a}.\]<br />Pero <br />\[\int_{\gamma_1}f(z)dz=\int_{-\infty}^{\infty}\frac{xe^{ix}}{x^2+a^2}=\int_{-\infty}^{\infty}\frac{x\cos x}{x^2+a^2}dx+i\int_{-\infty}^{\infty}\frac{x\sin x}{x^2+a^2}dx.\]<br />Así, igualando parte imaginaria con parte imaginaria y aprovechandonos de la paridad de la función, concluimos que<br />\[\int_{0}^{\infty}\frac{x\sin x}{x^2+a^2}dx=\frac{1}{2}\int_{-\infty}^{\infty}\frac{x\sin x}{x^2+a^2}dx=\frac{\pi}{2}e^{-a}.\]<br />$ Sabes tengo dos dudas bastante estúpidas tal vez pero no me quiero quedar con ellas, la primera es que se sobreentiende que a<R cierto?, de lo contrario la integral sobre la curva cerrada valdría cero por el T. de Cauchy- Goursat. Y mi otra duda es como se llega: $TEX: \[\left\| {\frac{{i{R^2}}}{{{R^2}{e^{i2\theta }} + {a^2}}}} \right\| = \frac{{{R^2}}}{{{R^2} - {a^2}}}\]$ No logro verla u.u XD

Abu-Khalil Ver Perfil del Miembro Ver los mensajes de este miembro	Aug 29 2011, 08:05 PM Publicado: #4
Dios Matemático Supremo Grupo: Usuario FMAT Mensajes: 3.812 Registrado: 4-November 07 Desde: Santiago Miembro Nº: 12.213 Nacionalidad: Colegio/Liceo: Universidad: Sexo:	CITA(The Number of The Beast @ Aug 29 2011, 03:36 PM) Sabes tengo dos dudas bastante estúpidas tal vez pero no me quiero quedar con ellas, la primera es que se sobreentiende que a<R cierto?, de lo contrario la integral sobre la curva cerrada valdría cero por el T. de Cauchy- Goursat. Y mi otra duda es como se llega: $TEX: \[\left\| {\frac{{i{R^2}}}{{{R^2}{e^{i2\theta }} + {a^2}}}} \right\| = \frac{{{R^2}}}{{{R^2} - {a^2}}}\]$ No logro verla u.u XD Sí, se sobreentiende porque después se toma 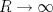$TEX: $R\to\infty$$ . Para la otra recuerda que $TEX: $\|x+y\|>\left\|\|x\|-\|y\|\right\|$$ . -------------------- ~milopez $TEX: \[\mathfrak{L}=\int_{-\infty}^\infty e^{-289x^2}dx=\frac{\Gamma (\frac{1}{2})}{17}=\frac{\sqrt{\pi}}{17}\]$ $TEX: <br />\begin{equation}\begin{aligned}<br />dS_t&=\mu S_t dt+\sqrt{V_t}S_t dW^S_t\\<br />dV_t&=\kappa(\theta-V_t)dt+\sigma\sqrt{V_t} dW^V_t\\<br />\end{aligned}\end{equation}<br />$ $TEX: <br />$$\mathbb A^{\text U}_M(N)$$<br />$

Nicky Belane Ver Perfil del Miembro Ver los mensajes de este miembro	Apr 14 2015, 02:13 PM Publicado: #5
Principiante Matemático Grupo: Usuario FMAT Mensajes: 3 Registrado: 14-April 15 Miembro Nº: 136.973 Nacionalidad:	$TEX: 1)Definimos $h(z)=\frac {f(z)}{z^{(n+1)}}$, sabemos que es analitica al reparar la singularidad, entonces alcanza su modulo maximo en el borde, luego tenemos que $\|h(z)\|\le \frac {M}{r^{(n+1)}}$, de donde se concluye la desigualdad buscada. Para la condicion para la igualdad basta ver que ella implica que el modulo de h es constante, y por el teorema del modulo maximo se sigue que es constante en todo el disco, luego se tiene el resultado buscado$ -------------------- Nosotros somos los muertos

« Posterior · Variable Compleja · Anterior »

Reply to this topic

Start new topic

1 usuario(s) está(n) leyendo esta discusión (1 invitado(s) y 0 usuario(s) anónimo(s))

0 miembro(s):

Modo de Ver: Estándar · Cambiar a: Lineal+ · Cambiar a: Outline

Suscribirse · Enviar por correo · Imprimir · Suscribirse a este foro

Versión Lo-Fi

Fecha y Hora actual: 4th April 2025 - 04:56 AM

Powered By IP.Board 2.2.1 © 2007 IPS, Inc.