I2 Probabilidades EYP1112 - Foro fmat.cl

Portal Matemático

¿Qué es FMAT?

Foro fmat.cl > Programa Enseñanza Universitaria > Comunidades Universitarias > Universidad Católica > Probabilidades y Estadística

Reply to this topic

Start new topic

I2 Probabilidades EYP1112, 2s 2008

DressedToKill Ver Perfil del Miembro Ver los mensajes de este miembro	Mar 30 2010, 06:39 PM Publicado: #1
Dios Matemático Supremo Grupo: Usuario FMAT Mensajes: 1.818 Registrado: 21-December 06 Miembro Nº: 3.434	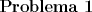$TEX: \bf{Problema 1}$ $TEX: \noindent<br />Existe una interesante relación entre la distribución Gamma y la distribución Poisson. Para ejemplificar esta relación consideremos la variable aleatoria $Z$ como el número de clientes que llegan a un Centro de pago en un intervalo de tiempo y $X_n$ el tiempo en que llega el $n$-ésimo cliente a la fila (si es que hay gente esperando, si no se atiende inmediatamente) desde que el encargado empezó a atender (suponga que no había nadie esperando que el encargado abriera).<br />\begin{enumerate}<br />\item[(a)] Si $X_3 \sim Gamma(3,1)$ muestre, usando técnicas de integración que<br />$$P(X_3 \ge x) = \dfrac{x^0 e^{-x}}{0!}+\dfrac{x^1 e^{-x}}{1!}+\dfrac{x^2 e^{-x}}{2!}.$$<br />\item[(b)] Si $Z \sim Poisson(x)$ muestre que $P(Z \le 2) = P(X_3 \ge x)$.<br />\item[©] Muestre que $P(X_{\alpha} > x) = P(Z \le \alpha-1=\displaystyle\sum_{y=0}^{\alpha-1}\dfrac{x^ye^{-x}}{y!}$ para $\alpha \in \mathbb{N}$, donde $Z \sim Poisson(x)$.<br />\end{enumerate}<br />$ $TEX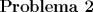: \bf{Problema 2}$ $TEX: \noindent<br />Considere las variables aleatorias $U_1$ y $U_2$, ambas distribuidas uniformemente en los intervalos $[0,1]$ y $[-\frac{\pi}{2},\frac{\pi}{2}]$ respectivamente.<br />\begin{enumerate}<br />\item[(a)] Sea $X = [n U_1]$ con $n \in \mathbb{N}$. Obtenga su función de probabilidad o densidad según corresponda.<br />\item[(b)] Sea $Y = \tan(U_2)$. Obtenga su función de probabilidad o densidad según corresponda.<br />\end{enumerate}<br />$ $TEX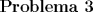: \bf{Problema 3}$ $TEX: \noindent<br />Sean $X$ e $Y$ variables aleatorias distribuidas conjuntamente con función densidad dada por<br /><br />$$f_{X,Y}(x,y) = c (x+2y), 0 < y < 1, 0 < x < 2$$<br />y $0$ en otro caso.<br />\begin{enumerate}<br />\item[(a)] Determine el valor de la constante $c$.<br />\item[(b)] Encuentre la función densidad marginal de $X$.<br />\item[©] Calcule la función de distribución acumulada conjunta de $X$ e $Y$.<br />\end{enumerate}<br />$ $TEX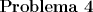: \bf{Problema 4}$ $TEX: \noindent<br />Un cartero recorre diariamente en bicicleta el sector asignado para repartir correspondencia. La distancia $X$ en kilómetros que debe recorrer para lograr entregar toda la correspondencia del día es una variable aleatoria de la cual se sabe que su logaritmo natural distribuye $Normal(0,1)$. Por otra parte se sabe que el cartero dada su edad y estado físico sólo es capaz de pedalear $x$ Km en un día. Suponiendo que la bicicleta del cartero recibe mantención día a día y en caso de fallar un auxiliar le lleva una bicicleta de repuesto para que siga con su trabajo.<br />\begin{enumerate}<br />\item[(a)] ¿Cuál es la probabilidad que en un día cualquiera no logre cumplir con la entrega de toda su correspondencia?<br />\item[(b)] Determine el valor de $c$ para que el $80\%$ de los días laborales el cartero pedalee a lo más $c$ kilómetros.<br />\item[©] Si el cartero trabaja de lunes a sábado, ¿cuál es la probabilidad que en una semana sin festivos el cartero logre al menos una jornada perfecta?<br />\end{enumerate}<br />$ Otra prueba larga. -------------------- http://www.youtube.com/watch?v=sp_WV91jx8E...feature=related

Abu-Khalil Ver Perfil del Miembro Ver los mensajes de este miembro	May 6 2010, 05:11 PM Publicado: #2
Dios Matemático Supremo Grupo: Usuario FMAT Mensajes: 3.812 Registrado: 4-November 07 Desde: Santiago Miembro Nº: 12.213 Nacionalidad: Colegio/Liceo: Universidad: Sexo:	P1a $TEX: \noindent Dado que $X_3\sim\text{Gamma}(3,1)$,<br />\[P\left(X_3\geq x\right)=1-P\left(X_3<x\right)=1-\int_0^x\frac{1^3t^{3-1}e^{-t}}{\Gamma(3)}dt=1-\frac{1}{2}\int_0^xt^2e^{-t}dt.\]<br />Integrando por partes,<br />\begin{equation}\begin{aligned}\int_0^xt^2e^{-t}dt<br />&=\left.-e^{-t}t^2\right\|^x_0+2\int_0^xte^{-tdt}=-x^2e^{-x}+2\left(\left.-e^{-t}t\right\|^x_0+\int_0^xe^{-tdt}\right)\\<br />&=-x^2e^{-x}+2\left(\left.-e^{-t}t\right\|^x_0\left.-e^{-t}t\right\|^x_0\right)=-x^2e^{-x}-2e^{-x}-2xe^{-x}+2.<br />\end{aligned}\end{equation}<br />Reemplazando, <br />\[P\left(X_3\geq x\right)=1-\frac{1}{2}\left(-x^2e^{-x}-2e^{-x}-2xe^{-x}+2\right)=e^{-x}+xe^{-x}+\frac{x^2e^{-x}}{2}. \ \square\]<br />$ P1b $TEX: \noindent Como $Z\sim\text{Poisson}(x)$, usando (a) se tiene que<br />\[P\left(Z\leq 2\right)=\sum_{k=0}^2\frac{x^ke^{-x}}{k!}=P\left(X_3\geq x\right). \ \square\]<br />$ P1c $TEX: \noindent Como $X_{\alpha}\sim\text{Gamma}\left(\alpha,1\right),$ probaremos por inducción lo pedido.<br />\begin{enumerate}<br />\item[(i)]Si $\alpha=1\Rightarrow P\left(X_1\geq x\right)=1-\int_0^xe^{-t}dt=e^{-x}=\displaystyle\sum_{k=0}^{1-1}\frac{x^k e^{-x}}{k!}$.<br />\item[(ii)]Supongamos que es cierto para algún $n\in\mathbb{N}$. Mostraremos que<br />\[P\left(X_{\alpha+1}\geq 1\right)=P\left(Z-\alpha\right)=\sum_{k=0}^{\alpha}\frac{x^ke^{-x}}{k!}.\]<br />En efecto,<br />\begin{equation}\begin{aligned}<br />P\left(X_{\alpha+1}\geq 1\right)&=1-\int_0^x\frac{t^{\alpha}e^{-t}}{\Gamma\left(\alpha+1\right)}dt=1-\frac{1}{\Gamma\left(\alpha+1\right)}\left\{\left.\left(-e^{-t}t^\alpha\right)\right\|^x_0+\alpha\int_0^xt^{\alpha-1}e^{-t}dt\right\}\\<br />&=\frac{x^\alpha e^{-x}}{\alpha!}+\left(1-\int_0^x\frac{t^{\alpha-1}e^{-t}dt}{\Gamma\left(\alpha\right)}dt\right)=\frac{x^\alpha e^{-x}}{\alpha!}+P\left(X_{\alpha}\geq 1\right)\\<br />&=\frac{x^\alpha e^{-x}}{\alpha!}+\sum_{k=0}^{\alpha-1}\frac{x^ke^{-x}}{k!}=\sum_{k=0}^{\alpha}\frac{x^ke^{-x}}{k!}. \ \square<br />\end{aligned}\end{equation}<br />\end{enumerate}<br />$ P2b $TEX: \noindent Dado que $U_2$ esta distribuida uniformemente, tenemos que<br />\[f_U(u)=\frac{1}{\pi},u\in\left[-\frac{\pi}{2},\frac{\pi}{2}\right].\]<br />Luego,<br />\[F_Y(y)=\int_{-\frac{\pi}{2}}^{\arctan y}f_U(u)du=\int_{-\frac{\pi}{2}}^{\arctan y}\frac{du}{\pi}.\]<br />Poniendo $\arctan y=u$, tenemos que<br />\[F_Y(y)=\int_{-\infty}^y\frac{dy}{\pi\left(1+y^2\right)}\Rightarrow f_Y(y)=\frac{dF_Y}{dy}=\frac{1}{\pi\left(1+y^2\right)},-\infty<y<\infty.\]<br />$ P3a $TEX: \noindent Se debe cumplir que<br />\[\iint_{\mathbb{R}^2}f_{X,Y}(x,y)dA=1,\]<br />es decir,<br />\[\int_0^1\int_0^2c(x+2y)dxdy=1.\]<br />Calculando la integral se concluye que $c=\frac{1}{4}$.<br />$ P3b $TEX: \noindent Sabemos que<br />\[f_X(x)=\int_\mathbb{R}f_{X,Y}(x,y)dy=\int_0^1\frac{1}{4}(x+2y)dy=\frac{x}{4}+\frac{1}{4},0\leq x\leq 2.\]<br />$ P3c $TEX: \noindent Por definición,<br />\[F_{X,Y}(x,y)=\int_0^y\int_0^xf_{X,Y}(u,v)dudv=\int_0^y\int_0^x\frac{1}{4}\left(u+2v\right)dudv=\frac{xy}{8}\left(x+2y\right),(x,y)\in[0,2]\times[0,1].\]<br />$ P4a $TEX: \noindent Como $X\sim\text{Normal}(0,1)$, entonces <br />\[P\left(X\leq x\right)=\Phi(x).\]<br />$ P4b $TEX: \noindent Como $X\sim\text{Normal}(0,1)$, entonces <br />\[P\left(X\leq c\right)=0.8\iff \Phi©=0,8\iff c=\Phi^{-1}\left(0,8\right)=0,85.\]<br />$ P4c $TEX: \noindent Definamos $Y:\#$ de jornadas perfectas, entonces<br />\[P\left(Y\geq 1\right)=1-P\left(Y=0\right)=1-\left(1-\Phi\left(x\right)\right)^6.\]$ -------------------- ~milopez $TEX: \[\mathfrak{L}=\int_{-\infty}^\infty e^{-289x^2}dx=\frac{\Gamma (\frac{1}{2})}{17}=\frac{\sqrt{\pi}}{17}\]$ $TEX: <br />\begin{equation}\begin{aligned}<br />dS_t&=\mu S_t dt+\sqrt{V_t}S_t dW^S_t\\<br />dV_t&=\kappa(\theta-V_t)dt+\sigma\sqrt{V_t} dW^V_t\\<br />\end{aligned}\end{equation}<br />$ $TEX: <br />$$\mathbb A^{\text U}_M(N)$$<br />$

« Posterior · Probabilidades y Estadística · Anterior »

Reply to this topic

Start new topic

1 usuario(s) está(n) leyendo esta discusión (1 invitado(s) y 0 usuario(s) anónimo(s))

0 miembro(s):

Modo de Ver: Estándar · Cambiar a: Lineal+ · Cambiar a: Outline

Suscribirse · Enviar por correo · Imprimir · Suscribirse a este foro

Versión Lo-Fi

Fecha y Hora actual: 23rd November 2024 - 07:00 PM

Powered By IP.Board 2.2.1 © 2007 IPS, Inc.