esta si tengo duda de como se hace

esta si tengo duda de como se hace, integral compleja

ccmagnus Ver Perfil del Miembro Ver los mensajes de este miembro	Mar 23 2010, 11:20 PM Publicado: #1
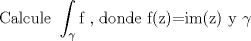Maestro Matemático Grupo: Usuario FMAT Mensajes: 92 Registrado: 11-October 08 Miembro Nº: 35.894 Nacionalidad: Colegio/Liceo: Universidad: Sexo:	soy nuevo en variable ,se los agradecere si me ayudan con esta 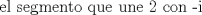$TEX: $$\text{Calcule }\int _{\gamma }\text{f , donde f(z)=im(z) y }\gamma \text{ }$$$ $TEX: $$\text{el segmento que une 2 con -i}$$$ ¿Se cumplira que 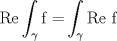$TEX: $$\text{Re}\int _{\gamma }\text{f =}\int _{\gamma }\text{Re f}$$$ ?

coquitao Ver Perfil del Miembro Ver los mensajes de este miembro	Mar 23 2010, 11:55 PM Publicado: #2
Dios Matemático Supremo Grupo: Super Moderador Mensajes: 2.065 Registrado: 25-May 08 Desde: Pelotillehue Miembro Nº: 24.463	Es sólo por definición de integral de contorno: 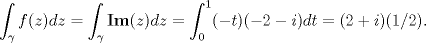$TEX: $\displaystyle \int_{\gamma} f(z) dz = \displaystyle \int_{\gamma} \mathbf{Im} (z) dz = \int_{0}^{1} (-t) (-2-i) dt = (2+i)(1/2).$$ ¿Claro lo anterior? Pregunto para poder seguir. De no ser así, para que continuar, ¿no crees? -------------------- "Please forget everything you have learned in school; for you haven't learned it... Please keep in mind at all times the corresponding portions of your school curriculum; for you haven't actually forgotten them." -- E. Landau

ccmagnus Ver Perfil del Miembro Ver los mensajes de este miembro	Mar 24 2010, 11:42 PM Publicado: #3
Maestro Matemático Grupo: Usuario FMAT Mensajes: 92 Registrado: 11-October 08 Miembro Nº: 35.894 Nacionalidad: Colegio/Liceo: Universidad: Sexo:	Si pero creo que la integral va de 0 a 2 y no veo porque va de 0 a1

coquitao Ver Perfil del Miembro Ver los mensajes de este miembro	Mar 24 2010, 11:48 PM Publicado: #4
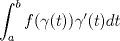Dios Matemático Supremo Grupo: Super Moderador Mensajes: 2.065 Registrado: 25-May 08 Desde: Pelotillehue Miembro Nº: 24.463	La integral de f a lo largo de la curva $TEX: $\gamma : [a,b] \to \mathbb{C}$$ es (por definición) $TEX: $\displaystyle \int_{a}^{b} f(\gamma(t)) \gamma^{\prime}(t) dt$$ ... () En tu caso, no es que quieras integrar de 2 a -i, sino a lo largo del segmento de recta que une ambos puntos. Luego, lo primero es dar la parametrización del segmento. Yo digo que es 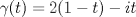$TEX: $\gamma(t) = 2(1-t) - it$$ cuando t varía entre 0 y 1. ¿De acuerdo? Aplica ahora la fórmula en (). -------------------- "Please forget everything you have learned in school; for you haven't learned it... Please keep in mind at all times the corresponding portions of your school curriculum; for you haven't actually forgotten them." -- E. Landau

1 usuario(s) está(n) leyendo esta discusión (1 invitado(s) y 0 usuario(s) anónimo(s))

0 miembro(s):

Modo de Ver: Estándar · Cambiar a: Lineal+ · Cambiar a: Outline

Fecha y Hora actual: 23rd November 2024 - 05:47 PM