Propuesto maomeno - Foro fmat.cl

Foro fmat.cl > Programa Enseñanza Universitaria > Ejercitación > Álgebra > Teoría de Conjuntos

Propuesto maomeno, Relación de orden

Opciones

PsicoStitch Ver Perfil del Miembro Ver los mensajes de este miembro	Mar 21 2010, 01:47 AM Publicado: #1
Dios Matemático Supremo Grupo: Usuario FMAT Mensajes: 699 Registrado: 6-May 07 Miembro Nº: 5.650 Nacionalidad: Colegio/Liceo: Universidad: Sexo:	$TEX: <br />Dos conjuntos $X$ e $Y$ se llamarán equivalentes, $X \sim Y$, si existe una biyección entre X e Y.<br /><br />Si $X$ e $Y$ son conjuntos tales que X es equivalente a un subconjunto de Y, escribiremos $$X \preceq Y .$$<br /><br />Demostrar que la relación $\preceq$ es de orden en $\mathcal{P}(E)$ para algún conjunto E.\\<br /><br />PS: La antisimetría corresponde al teorema de Schröder-Bernstein. Propongo el ejercicio para ver una demostración distinta a la que conozco. Si alguien quiere agregar la demostración de que además la relación es de orden total, bienvenido sea.<br />$ --------------------

Kaissa Ver Perfil del Miembro Ver los mensajes de este miembro	Mar 21 2010, 12:55 PM Publicado: #2
Dios Matemático Supremo Grupo: Usuario FMAT Mensajes: 9.897 Registrado: 6-April 08 Miembro Nº: 19.238 Nacionalidad: Colegio/Liceo: Sexo:	$TEX: $ $\\<br />La definici\'on brindada por PsicosTitch es equivalente a<br />\begin{eqnarray}<br />X\preceq Y\Longleftrightarrow \sharp X\leq \sharp Y<br />\end{eqnarray}<br />Bien poco puedo aportar, disculpa, pero solo conozco la demostraci\'on usual que se fundamenta en la equivalencia que he mostrado ac\'a.\\<br />Para ver que el orden es total simplemente observamos que si $A$ y $B$ son subconjuntos de $E$; entonces $\sharp A$ y $\sharp B$ son naturales (si alguno de los conjuntos es infinito consideramos el cardinal como algun alef) y los naturales son comparables.$ -------------------- Este es un extracto de Qué es fmat by Kenshin. La pregunta para ti estimado(a) lector(a) es... ¿Qué haces tu para que ésto se cumpla?

aleph_omega Ver Perfil del Miembro Ver los mensajes de este miembro	Mar 21 2010, 01:21 PM Publicado: #3
Dios Matemático Supremo Grupo: Usuario FMAT Mensajes: 560 Registrado: 24-December 09 Miembro Nº: 64.629	Lema: 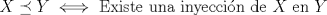$TEX: $X\preceq Y \iff$ Existe una inyección de $X$ en $Y$$ Demostración: $TEX: \noindent Se tiene que $X\preceq Y$ si $\exists Y_1\subseteq Y: X\sim Y_1$ y por lo tanto tenemos que existe una biyección de $X$ a $Y_1$. Sea $f:X\to Y_1$ esta biyección. Consideramos la extensión $f_1:X\to Y$ como la misma $f$, que por supuesto es inyectiva pero puede no ser es sobre pues puede existir un elemento de $Y$ que no tiene preimagen.<br /><br />Por otro lado sea $g:X\to Y$ una inyección. Sea $S:=\{y\in Y: y\notin im(g) \}$. Luego se tiene que $\hat{g}:X\to Y\setminus S$ definida dela misma forma que $g$ es una biyección.$ Para demostrar que es de orden, falta mostrar la reflexividad y la transitividad,pues la anstisimetría "ya está demostrada" con SB ( la demostración que conozco yo es en función de inyecciones, es decir, si existe inyección de E en F y una inyección de F en E entonces existe biyección entre E y F) Para la reflexividad, basta tomar la función identidad, que por su puesto es inyectiva. Para la transitividad , tomamos la composición entre inyecciones, que es inyectiva: $TEX: \noindent Sea $g:X\to Y$ y $h:Y\to Z$ funciones inyectivas. Queremos demostrar que $h\circ g:X\to Z$ es inyectiva. Para esto sean $a,b\in X$ tales que $(h\circ g)(a)=(h\circ g)(b)$. Es decir tenemos $h(g(a))=h(g(b))$ pero como $h$ es inyectiva, esto implica que $g(a)=g(b)$ y por la misma razón se tiene que $a=b$ y asi tenemos que la composición es inyectiva.<br />$ saludos Mensaje modificado por aleph_omega el Mar 21 2010, 01:22 PM

PsicoStitch Ver Perfil del Miembro Ver los mensajes de este miembro	Mar 21 2010, 01:26 PM Publicado: #4
Dios Matemático Supremo Grupo: Usuario FMAT Mensajes: 699 Registrado: 6-May 07 Miembro Nº: 5.650 Nacionalidad: Colegio/Liceo: Universidad: Sexo:	Mi idea era inicial era ver demostraciones de SB, todo el resto lo puse para redondear el problema xD. EDIT: lo del orden total tampoco es tan trivial, pues es equivalente al axioma de elección según tengo entendido. Mensaje modificado por PsicoStitch el Mar 21 2010, 01:31 PM --------------------

aleph_omega Ver Perfil del Miembro Ver los mensajes de este miembro	Mar 21 2010, 01:30 PM Publicado: #5
Dios Matemático Supremo Grupo: Usuario FMAT Mensajes: 560 Registrado: 24-December 09 Miembro Nº: 64.629	Okei, esa demostración es hermosa, trataré de acordarme de como era. ( la construcción de la biyección es en función de ambas inyecciones obviamente) saludos Mensaje modificado por aleph_omega el Mar 21 2010, 01:31 PM

Kaissa Ver Perfil del Miembro Ver los mensajes de este miembro	Mar 22 2010, 08:53 PM Publicado: #6
Dios Matemático Supremo Grupo: Usuario FMAT Mensajes: 9.897 Registrado: 6-April 08 Miembro Nº: 19.238 Nacionalidad: Colegio/Liceo: Sexo:	es bacan!!! sale en el paul halmos y habla de ansestros y descendientes xdd es muy seco ese autor -------------------- Este es un extracto de Qué es fmat by Kenshin. La pregunta para ti estimado(a) lector(a) es... ¿Qué haces tu para que ésto se cumpla?

PsicoStitch Ver Perfil del Miembro Ver los mensajes de este miembro	Mar 22 2010, 09:10 PM Publicado: #7
Dios Matemático Supremo Grupo: Usuario FMAT Mensajes: 699 Registrado: 6-May 07 Miembro Nº: 5.650 Nacionalidad: Colegio/Liceo: Universidad: Sexo:	CITA(Kaissa @ Mar 22 2010, 10:53 PM) es bacan!!! sale en el paul halmos y habla de ansestros y descendientes xdd es muy seco ese autor jajajaja si esa es la que yo conozco, es filete PD: penultimo post O.O! --------------------

« Posterior · Teoría de Conjuntos · Anterior »

1 usuario(s) está(n) leyendo esta discusión (1 invitado(s) y 0 usuario(s) anónimo(s))

0 miembro(s):

Modo de Ver: Estándar · Cambiar a: Lineal+ · Cambiar a: Outline

Suscribirse · Enviar por correo · Imprimir · Suscribirse a este foro

Versión Lo-Fi

Fecha y Hora actual: 26th April 2025 - 12:12 AM