|
|
|
|
|
|
|
 Mar 13 2010, 09:15 PM Mar 13 2010, 09:15 PM
Publicado:
#1
|
|
 Dios Matemático Supremo Grupo: Usuario FMAT Mensajes: 1.564 Registrado: 12-November 07 Desde: La Union, XIV Region de los Rios Miembro Nº: 12.607 Nacionalidad:  Colegio/Liceo:  Universidad:  Sexo:  |
33ª OLIMPIADA INTERNACIONAL DE MATEMÁTICA Moscú, Rusia, 1992 Primera Prueba: 15 de julio de 1992 Problema 1: Encuentre todas las ternas 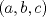 de enteros, con de enteros, con 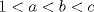 tales que tales que 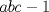 es un múltiplo de es un múltiplo de 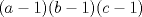 Problema 2: Encuentre todas las funciones 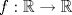 tales que: tales que: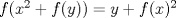 para todo para todo 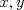 en en 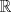 Problema 3: Dados 9 puntos en el espacio, tales que no existan cuatro de ellos coplanares, encuentre el menor natural  tales que para cualquier coloracion con azul y blanco de tales que para cualquier coloracion con azul y blanco de  aristas dibujadas entre esos 9 puntos, exista siempre un triángulo monocromático. aristas dibujadas entre esos 9 puntos, exista siempre un triángulo monocromático.Segunda Prueba: 16 de julio de 1992 Problema 4: En el plano, sea 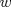 una circunferencia fija, una circunferencia fija,  una recta tangente a una recta tangente a 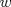 y y 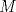 un punto sobre un punto sobre  . Encuentre el lugar geométrico de los puntos . Encuentre el lugar geométrico de los puntos 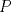 para los cuales existen dos puntos para los cuales existen dos puntos 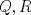 sobre sobre  tales que tales que 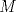 es el punto medio de es el punto medio de 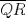 y y 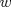 es el incírculo del es el incírculo del 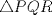 Problema 5: Sea 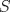 un subconjunto finito del espacio euclídeo de los puntos un subconjunto finito del espacio euclídeo de los puntos 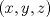 con coordenadas enteras. Llamemos con coordenadas enteras. Llamemos 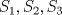 a las proyecciones de a las proyecciones de 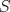 sobre los planos sobre los planos 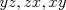 , respectivamente. Si , respectivamente. Si 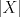 denota la cardinalidad del conjunto denota la cardinalidad del conjunto 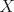 , pruebe que: , pruebe que: 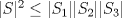 Problema 6: Para cada entero positivo  , denotemos por , denotemos por 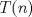 al mayor entero tal que para todo entero positivo al mayor entero tal que para todo entero positivo 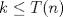 , , 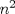 puede ser escrito como la suma de puede ser escrito como la suma de 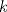 cuadrados perfectos. cuadrados perfectos. a) Pruebe que para todo 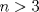 , se cumple que , se cumple que 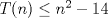 b) Encuentre un natural  tal que tal que 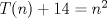 c) Demuestre que la ecuacion 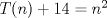 admite infinitas soluciones en los enteros positivos admite infinitas soluciones en los enteros positivosResumen de soluciones Cualquier error de traduccion, o detalle que no se entienda, favor enviar MP. Recordar que los enunciados no son textuales. Saludos. -------------------- Ricardo Vargas Obando
Ex-alumno Deutsche Schule La Unión (Generación 2010, de los 150 años). Novato de Licenciatura en Matemática/Estadística, en la Pontificia Universidad Católica de Chile.  Grupo de facebook de Novatos Matemática y Estadística PUC 2011 Currículum Olímpico:
|
|
|
|
 |
Respuestas
 Jan 25 2014, 11:16 AM Jan 25 2014, 11:16 AM
Publicado:
#2
|
|
|
Dios Matemático Supremo Grupo: Usuario FMAT Mensajes: 9.897 Registrado: 6-April 08 Miembro Nº: 19.238 Nacionalidad:  Colegio/Liceo:  Sexo:  |
relax, el lema es bien sabido y la demo la hallas en varios lugares... Entre ellos el pdf "three geometric lemmas"
-------------------- |
|
|
|
Mensajes en este tema
 ~Fatal_Collapse~ XXXIII IMO (1992) Mar 13 2010, 09:15 PM
~Fatal_Collapse~ XXXIII IMO (1992) Mar 13 2010, 09:15 PM
 Diego Navarro SP3:
Vease desde el segundo parrafo en adelante de... Sep 30 2010, 06:52 PM
Diego Navarro SP3:
Vease desde el segundo parrafo en adelante de... Sep 30 2010, 06:52 PM
 Emi_C [color=#FF0000][b]Problema 2: Encuentre todas las ... Oct 10 2010, 05:14 PM
Emi_C [color=#FF0000][b]Problema 2: Encuentre todas las ... Oct 10 2010, 05:14 PM
 Pedantic Anarchy Problema 1:Como 1<a<b<c, si a>3 se ti... Jan 18 2011, 05:25 PM
Pedantic Anarchy Problema 1:Como 1<a<b<c, si a>3 se ti... Jan 18 2011, 05:25 PM
 asdayuyi Pal 4
Antes que nada enunciaremos un lema que nos... Jan 25 2014, 12:18 AM
asdayuyi Pal 4
Antes que nada enunciaremos un lema que nos... Jan 25 2014, 12:18 AM  |
2 usuario(s) está(n) leyendo esta discusión (2 invitado(s) y 0 usuario(s) anónimo(s))
0 miembro(s):
| Versión Lo-Fi | Fecha y Hora actual: 8th April 2025 - 02:24 AM |











