|
|
|
|
|
|
|
  |
 Mar 13 2010, 12:48 PM Mar 13 2010, 12:48 PM
Publicado:
#1
|
|
|
Dios Matemático Grupo: Team Ensayos FMAT Mensajes: 274 Registrado: 30-December 09 Miembro Nº: 64.740 Nacionalidad:  Colegio/Liceo:  Sexo:  |
3ª OLIMPIADA INTERNACIONAL DE MATEMÁTICA Veszprém, Hungría, 1961 Primera Prueba: Lunes 6 de julio de 1961 Problema 1: Resolver el siguiente sistema de ecuaciones: 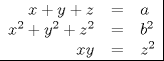 donde  y y  son constantes. De también las condiciones que deben cumplir son constantes. De también las condiciones que deben cumplir  y y  para que las soluciones del sistema sean números positivos distintos. para que las soluciones del sistema sean números positivos distintos.Problema 2: Sean  , ,  y y  los lados de un triángulo y los lados de un triángulo y 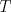 su área. Probar que su área. Probar que 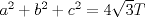 . ¿En qué casos se cumple ésta igualdad? . ¿En qué casos se cumple ésta igualdad?Problema 3: Resolver la ecuación 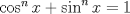 , donde , donde 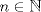 . .Segunda Prueba: Jueves 16 de julio de 1961 Problema 4: Considere un triángulo 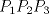 y un punto y un punto 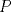 dentro del triángulo. Las rectas dentro del triángulo. Las rectas 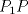 , , 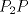 y y 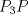 intercectan al lado opuesto en los puntos intercectan al lado opuesto en los puntos 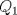 , , 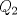 y y 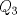 , respectivamente. Probar que, de los números de: , respectivamente. Probar que, de los números de: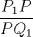 , , 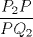 , , 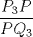 al menos uno sea 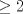 y al menos uno sea y al menos uno sea 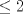 . .Problema 5: Construír un triángulo 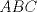 si si 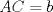 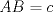 y y 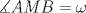 , donde , donde 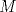 es el punto medio de es el punto medio de 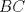 y y 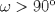 . Probar que una solución exista si y solo si: . Probar que una solución exista si y solo si: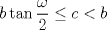 ¿En qué casos se cumple esta igualdad? Problema 6: Considere un plano  y tres puntos no colineales y tres puntos no colineales 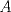 , , 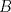 y y 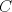 en el mismo lado de en el mismo lado de  . Suponga que el plano determinado por estos tres puntos no es paralelo a . Suponga que el plano determinado por estos tres puntos no es paralelo a  . En el plano se toman tres puntos arbitrarios . En el plano se toman tres puntos arbitrarios 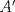 , , 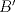 y y 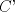 . Sean . Sean 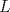 , , 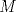 y y 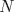 los puntos medios de los segmentos los puntos medios de los segmentos 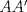 , , 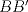 y y 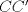 . Sea G el centroide del triángulo . Sea G el centroide del triángulo 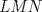 (Nótese que no consideramos las posiciones de (Nótese que no consideramos las posiciones de 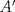 , , 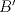 y y 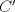 en las que éstas no forman un triángulo). ¿Cuál es el lugar geométrico del punto en las que éstas no forman un triángulo). ¿Cuál es el lugar geométrico del punto 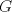 ya que ya que 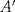 , , 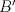 y y 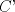 varían independientemente en el plano varían independientemente en el plano  . .Resumen de soluciones Mensaje modificado por einstenio16 el Jan 12 2023, 11:14 AM -------------------- He vuelto con las pilas cargaditas!!! |
|
|
|
 Feb 27 2011, 03:14 PM Feb 27 2011, 03:14 PM
Publicado:
#2
|
|
 Dios Matemático Supremo Grupo: Team Ensayos FMAT Mensajes: 513 Registrado: 25-April 08 Desde: CSMC Miembro Nº: 21.189 Nacionalidad:  Colegio/Liceo:  Sexo:  |
En la pregunta 2 deberia decir
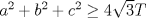
-------------------- FunGeometry
SIEMPRE CON LAS MEJORES INTENCIONES DE AYUDAR. ATTE. NABODORBUCO EL TERCER OJO GoGeometry LA IDEA ES QUE NO ESPERES QUE FMAT RESUELVA TUS TAREAS, ESCRIBE SIEMPRE CUALES SON TUS INQUIETUDES |
|
|
|
 May 24 2011, 05:18 PM May 24 2011, 05:18 PM
Publicado:
#3
|
|
 Dios Matemático Grupo: Usuario FMAT Mensajes: 270 Registrado: 31-May 10 Desde: San antonio Miembro Nº: 71.730 Nacionalidad:  Colegio/Liceo:  Universidad:  Sexo:  |
eso mismo pensé después de haber postiado xD
Mensaje modificado por luis_fz el May 24 2011, 05:59 PM |
|
|
|
 May 24 2011, 05:52 PM May 24 2011, 05:52 PM
Publicado:
#4
|
|
|
Dios Matemático Supremo Grupo: Usuario FMAT Mensajes: 2.818 Registrado: 3-October 09 Miembro Nº: 59.773 Nacionalidad:  Colegio/Liceo:  Universidad:  Sexo:  |
Solo
 es natural, los catetos no necesariamente. es natural, los catetos no necesariamente.Recuerda que FLT dice: Si tienes 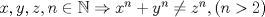 Saludos. Mensaje modificado por El Geek el May 25 2011, 12:27 AM -------------------- Me voy, me jui.
|
|
|
|
| master_c |
 May 25 2011, 08:20 PM May 25 2011, 08:20 PM
Publicado:
#5
|
|
Invitado |
Como a ni b no son fijos, dividimos el sistema en tres casos
caso 1) si 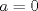 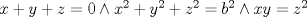 mezclando la ec.1 con la ec.2 se tiene que 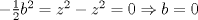 Entonces se obtiene un sistema trivial en el cual 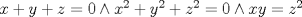 mezclando la ec.3 con la ec.2 es trivial que 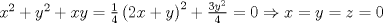 por tanto si por tanto si 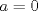 implica necesariamente que implica necesariamente que 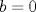 y se obtiene una solucion trivial la cual no cumple con el requisito del problema y se obtiene una solucion trivial la cual no cumple con el requisito del problemacaso 2) si 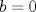 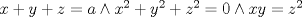 mezclando la ec.1 con la ec.2 se tiene 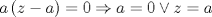 de aqui de derivan dos casos mas en el primero se obtiene idem anterior el cual se probo que no nos sirve, basta solo analizar el segundo caso si de aqui de derivan dos casos mas en el primero se obtiene idem anterior el cual se probo que no nos sirve, basta solo analizar el segundo caso si  se tiene se tiene 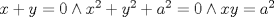 mezclando ecs se obtiene que mezclando ecs se obtiene que 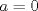 y se llega al caso 1 y se llega al caso 1 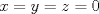 el cual no nos interesa por lo tanto para ambos casos independientemente de cual se elija como nulo siempre se termina llegando a que la otra constante sea nula y no viene al caso entonces, sabemos que para que se cumpla la condicion de que las soluciones del sistema sean distintas y positivas a y b deben ser no nulos por separado o ambos ala vez. el cual no nos interesa por lo tanto para ambos casos independientemente de cual se elija como nulo siempre se termina llegando a que la otra constante sea nula y no viene al caso entonces, sabemos que para que se cumpla la condicion de que las soluciones del sistema sean distintas y positivas a y b deben ser no nulos por separado o ambos ala vez.ahora si a y b son no nulos tenemos el sistema 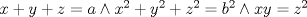 caso 3) 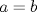 se encuentra rapidamente que se encuentra rapidamente que 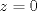 y las soluciones al sistema son 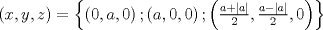 las primeras dos soluciones no nos sirven ya que no son ni positivas ni distintas para ninguna a, la tercera solucion es distinta para todo a no nulo, pero 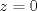 no cumple la condicion ya que no es positivo. no cumple la condicion ya que no es positivo.caso 4) 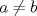 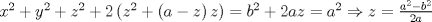 puesto que a es no nulo tenemos el sistema puesto que a es no nulo tenemos el sistema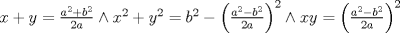 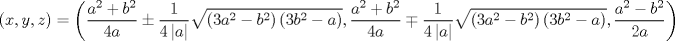 ahora faltaria decidir cuando es positiva y distinta, mas rato cuando tenga tiempo termino... Mensaje modificado por master_c el May 25 2011, 08:23 PM |
|
|
|
 Jan 24 2016, 03:29 PM Jan 24 2016, 03:29 PM
Publicado:
#6
|
|
|
Principiante Matemático Grupo: Usuario FMAT Mensajes: 10 Registrado: 30-December 14 Desde: Ovalle Miembro Nº: 135.058 Nacionalidad:  Colegio/Liceo:  Universidad:  Sexo:  |
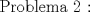 Sea 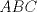 un triangulo cualquiera digamos un triangulo cualquiera digamos  el mayor de sus catetos, a la vez sea el mayor de sus catetos, a la vez sea 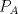 el pie de la altura desde el pie de la altura desde 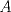 . Definamos . Definamos   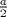 e e 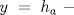 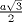 . Aplicando Pitagoras a los triangulos . Aplicando Pitagoras a los triangulos 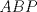 y y 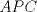 tenemos que : tenemos que : 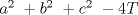 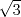  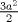 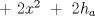 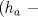 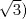  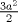 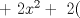 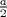 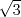 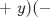 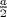 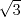 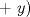 La trabajamos un poco y llegamos a la expresion : 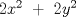 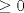 probando lo pedido. probando lo pedido.La igualdad se da cuando 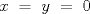 que seria el caso del triangulo equilatero. que seria el caso del triangulo equilatero. Corriganme si hay algun error Mensaje modificado por panchovega_ el Jan 24 2016, 03:35 PM |
|
|
|
  |
1 usuario(s) está(n) leyendo esta discusión (1 invitado(s) y 0 usuario(s) anónimo(s))
0 miembro(s):
| Versión Lo-Fi | Fecha y Hora actual: 8th July 2025 - 02:26 AM |








